Transformada de Fourier
¿Qué hay detrás del caro equipo de científicos? ¿Cómo procesan los datos que reciben estas máquinas? En general, no nos importa mucho. Un ordenador recogerá las mediciones y reflejará los resultados mediante un gráfico moderno. Además, cuanto más caro sea el utillaje, más preciso y mejor.

Desde este punto de vista, queda mucho trabajo oculto. ¿Cómo ha ocurrido este proceso? Aunque el ordenador es muy potente, hay que enseñarle cómo debe hacer el trabajo. Para que los datos sean externalizados, es necesario prepararlos para realizar tratamientos complejos. En casi todos los campos de la ciencia, este laborioso trabajo lo preparan los matemáticos y en mediciones con datos oscilantes se utiliza además la transformada de Fourier.
Temblores de la Tierra
Seguiremos un ejemplo de lo que inventó el matemático Joseph Fourier. Supongamos que un sismógrafo digital se pone en marcha en un territorio donde se producen muchos terremotos. Este dispositivo mide constantemente el movimiento del suelo, registrando en cada medida el desplazamiento desde el equilibrio, detectando los terremotos mediante vibraciones. También se deben medir las menores ondas sísmicas, lo que permite conocer la frecuencia e intensidad de la actividad.
Supongamos que el sismógrafo recibe 5 datos en un segundo, entonces habrá que acumular y procesar 432.000 números diarios.
Una sucesión de números no es muy útil. La verdad es que si se representa en un gráfico se ve mejor cuándo se han producido los terremotos y si han sido fuertes o no. Sin embargo, lo mejor para realizar operaciones y cálculos es que los números sean matemáticos. Esta función indica cómo se ha modificado la amplitud de la onda sísmica con el tiempo, es decir, es, en definitiva, un registro continuo de los movimientos de la tierra.
En eso consiste precisamente la mayor dificultad: ¿cómo se puede obtener una función que se ajuste bien a miles de puntos? ¿Es cierto que una sola fórmula matemática puede representar cualquier lista de números recibida? Cuando se trata de mediciones oscilatorias, se obtiene mediante la transformación de Fourier. El matemático francés ideó una metodología para superar fácilmente esta gran dificultad.
Curvas de aspecto complejo
El sismólogo puede dibujar los 432.000 puntos obtenidos a lo largo del día y, simplemente, entrelazando, obtendrá una curva. Pero si ese día ha habido actividad sísmica, esa curva será muy compleja. (Claro, si no hay actividad sísmica todas las mediciones serán cero y el trabajo del sismólogo no tendrá sentido). Sin embargo, con una curva tan compleja, es muy difícil calcular cualquier cosa.
El tratamiento de Fourier se basa en la descomposición de esta compleja curva. Según su teoría, cualquier función puede escribirse como la suma de los senos y los cosenos de distinta frecuencia. ¿Qué significa eso? Según esta idea, en lugar de calcular la función, se puede utilizar una suma de funciones simples. En la imagen se muestra un ejemplo de esta idea:
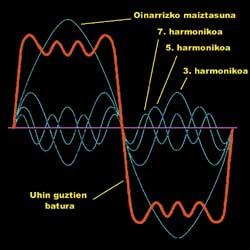
La función compleja (roja) es la suma de funciones simples (azules). En la imagen sólo hay cuatro funciones unidas, pero si se utilizan cientos, la suma puede ajustarse perfectamente a los datos experimentales recogidos.
Esta metodología facilita los cálculos pero tiene otras ventajas, permite el análisis de las frecuencias de los datos. Los términos de esta suma, esas "funciones simples", son oscilantes, pero cada una de ellas está relacionada con una frecuencia. Las frecuencias utilizadas en todos los términos son múltiplos de uno inicial. Puede decirse que una función simple representa la contribución de una determinada frecuencia en la función general que se desea buscar. Esto es muy útil para los científicos.
Por ejemplo, el sismólogo puede distinguir dos ondas sísmicas que se han producido simultáneamente, ya que cada una vibra con una frecuencia propia. Asimismo, puede detectar interferencias y despreciar los resultados del ruido de fondo del sismógrafo.
Espacio de frecuencia
El análisis de Fourier es igualmente útil en muchos otros ámbitos. El tratamiento del sonido es el ejemplo más claro. Cuando el sonido se graba digitalmente, el ruido de fondo es originado por la propia grabadora. El mero hecho de buscar la frecuencia de "limpieza" de ese sonido y de eliminar este término de la función hace que se elimine el ruido de la señal. En óptica, por ejemplo, en el tratamiento fotográfico.
La idea básica es, por tanto, descomponer una función compleja en funciones simples sinusoideas. En el lenguaje de los matemáticos, la función debe transformarse del espacio temporal al espacio de frecuencia. Esto significa que, a partir del tiempo de referencia inicial, el conjunto de frecuencias seleccionadas es el mismo. El procedimiento matemático para realizar este paso es el transformado de Fourier.
Matemático y egiptólogo
Si nos fijamos en la vida del matemático francés Jean Baptiste Joseph Fourier (1768-1830), XIX. La situación de Europa del siglo XX se refleja en la intensa actividad profesional que desarrolló, sobre todo en tres ámbitos. Siempre ejerció una gran actividad en matemáticas, política y arqueología.

Su fama de matemático es el XIX. desde principios del siglo. Con el objetivo de estudiar la conducción de calor en cuerpos bidimensionales, desarrolló una metodología con aplicación en casi todos los ámbitos de la ciencia. Actualmente esta metodología se denomina transformada de Fourier. Pero dedicó muchos años a desarrollar lo transformado: Comenzó en 1807 en Grenoble y terminó en París en 1822.
Entró en política de la mano de la Revolución Francesa. Napoleón participó en la expedición a Egipto, donde investigó los restos de la antigua civilización y, al volver a Francia, resumió lo aprendido en el libro Descripción de Egipto.
El éxito científico de la época Fourier le llevó a ser miembro de la Academia de la Ciencia, de la Academia Francesa y de la Academia de Medicina.
Aplicaciones ...
Comunicaciones

En las comunicaciones las señales son eléctricas, es decir, simplemente pulsos de tensión. Sin embargo, estas señales viajan a través de amplificadores, filtros y canales de comunicación, pudiendo alterar estas zonas de muchas maneras. La transformación de Fourier es imprescindible para entender cómo se producen estas transformaciones. En definitiva, estas señales eléctricas se gestionan en función de las frecuencias. En la señal digital (compuesta por 0 y 1) también es necesario diferenciar las frecuencias. Los pulsos de tensión de estas señales deben ajustarse al ancho de banda de las frecuencias, utilizando para ello la transformada de Fourier.
Sismología
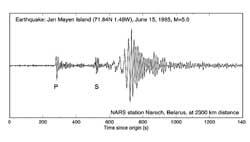
Las ondas sísmicas tienen frecuencias propias. Su análisis permite conocer el tipo y origen de las ondas. Este análisis se utiliza constantemente para investigar terremotos y placas tectónicas, pero no es la única aplicación. Entre otras cosas, en la industria del petróleo y el gas se ha utilizado mucho para buscar nuevas fuentes. Este tipo de investigación se utiliza para diferenciar las ondas sísmicas naturales de las provocadas por una explosión nuclear. Estas separaciones dependen de las frecuencias, por lo que la transformación de Fourier es imprescindible en el tratamiento matemático de los datos.
Sonar

Esta técnica sirve para detectar cualquier cosa en el agua. El funcionamiento básico es muy sencillo: se emiten ondas sonoras hacia el fondo y cuando choca contra algo, la onda rebota (eco). El análisis de la intensidad, frecuencia y tiempo de reflexión de la onda reflejada permite conocer la situación y naturaleza del objeto. El análisis de frecuencias se realiza mediante la transformación de Fourier.
Espectroscopia

La espectroscopia se utiliza para identificar los componentes químicos de una sustancia; cuando se aporta energía, cada molécula tiene una respuesta propia. La molécula "absorbe" o libera una determinada cantidad de energía mediante ondas electromagnéticas. El análisis de las frecuencias de estas ondas permite al químico identificar las moléculas.
Acústica

El sonido es una mezcla de muchas frecuencias. El timbre de un instrumento, por ejemplo, depende de las aportaciones de los armónicos. Por ello, cuando el sonido se convierte en señal eléctrica, el análisis de Fourier es imprescindible tanto en el tratamiento digital como en el analógico. Por ejemplo, la ecualización es actuar con intervalos de frecuencia.
Astronomía

Con el radiotelescopio se pueden ver cosas que no reflejan luces. Por ejemplo, la superficie de Venus está rodeada de una densa capa de nubes. Pero los astrónomos han podido explorar su superficie mediante ondas de radio. Es más, para calcular el periodo de rotación hay que tener en cuenta cómo se reflejan estas ondas en la superficie. Estos estudios requieren un análisis de frecuencias.
Óptica

La transformada de Fourier produce en la luz un efecto similar a un prisma: separa los componentes que contiene, es decir, los rayos de luz de diferente longitud de onda. Sin embargo, esto se hace matemáticamente, lo que significa que los efectos físicos de la luz pueden ser analizados matemáticamente. Por ejemplo, al pasar por una ranura, se puede conocer la influencia de la difracción en la luz. Este análisis aplicado a la luz visible sirve también para cualquier otra longitud de onda: microondas, rayos X, infrarrojos, etc.





