Como operar? (II). Multiplicación e división

En canto á multiplicación, hai que mencionar un caso particular. No produto manual mencionado anteriormente, dicíase que os dedos baixados nas mans multiplicábanse por 10.

Multiplicación

En canto á multiplicación, hai que mencionar un caso especial (que ten como produto o número 10). No produto manual mencionado anteriormente, dicíase que os dedos que baixaban nas mans multiplicábanse por 10 (mentalmente). Dentro deste cabezal está: o número de dedos que baixan dános a décima parte do produto.

Os egyptianos tamén sabían multiplicar por 10. Tras escribir un número paira iso, cada símbolo dunha orde era substituído por un símbolo de orde seguinte (figura 1).

Figura .

No sistema de numeración chinés tamén se pode ver a testemuña deste caso. Dependendo do lugar onde se poña o símbolo 10, pode ter dous significados diferentes (figura 2): si colócase á esquerda dos símbolos doutros números máis pequenos, tense suma. Si escríbese á dereita significa multiplicación.

Figura .

Vexamos como se realizaban outras multiplicacións.

Os egypti escribían 1 e o produto máis pequeno na parte superior de dúas columnas. Logo dobrábanse consecutivamente estes números e escribíanse debaixo. As dobraxes facíanse ata que na columna 1 obtíñase o outro produto (non o menor) ou, si non ocorrese, ata que aparecese o número máis grande que o outro produto. No primeiro caso aparecería o resultado xunto ao outro produto, na columna da dereita. No caso a) da figura 3 obtense o produto 128 x 12 = 1536. No segundo caso, na columna da esquerda (columna 1) seleccionábanse os números que sumaban o maior produto. O resultado obtíñase sumando na columna da dereita os números correspondentes aos números anteriores. No caso b) da figura 3 aparece o produto 369 x 19 = 4864 + 1216 + 608 + 304 + 19 = 7011.

Figura .

A multiplicación egyptiana era, por tanto, implea e non necesitaba táboas. Pero non foi o único método utilizado polos egyptianos. Tamén utilizaban o método denominado desdobramento. Nesta ocasión os dous produtos escribíanse na cabeza de dúas columnas, calculando a metade da máis grande (desprezando os restos) e os dobres da máis pequena e colocándoas nas columnas correspondentes. Na columna de pares sumáronse os correspondentes aos números impares da columna de medias, obtendo o produto. Na figura 4 pódese ver o produto 54 x 37 = 74 + 148 + 592 + 1184 = 1998. Este método tamén aparece nalgúns países da Unión Soviética.

Figura .

Os hindús usaban un ábaco de columna en area. Neste ábaco, na columna da dereita, escribían as unidades; cando estaba á súa esquerda as decenas; as porcentaxes á súa esquerda, etc. Deixaban en branco paira indicar a falta de unidades (figura 5).

Figura .

Este ábaco utilizábase paira realizar as multiplicacións. Por exemplo, paira calcular o produto 325 x 28 escribíanse nun ábaco de catro columnas, o maior na parte superior dereita e o segundo na parte inferior esquerda. No primeiro paso, calculaban (3 arriba) por (2 abaixo), 6 e escribían na columna esquerda do 3. A continuación (3 arriba) por (8 abaixo), 24, e no canto de 3 escribían 4 e engadían 2 ao 6 anterior.

O primeiro paso xa finalizara. Antes de comezar o segundo, o número inferior movíase por unha columna cara á dereita. Agora (2 arriba) calculábase por (2 abaixo), 4, e engadíase á 4 anterior (á esquerda da 2 superior). Daquela (2 arriba) por (8 abaixo), calcular e substituír o 2 por 6, eliminando o 2 e sumar 1 ao 8 que estaba á súa esquerda. Así acababa o segundo paso e una columna co número inferior cara á dereita. No terceiro paso (5) por (2 inferior), calcular 10; sumábanse 0 e 6 (5 esquerda) e 1 e 9 (6 esquerda), sendo o primeiro 6 e o segundo 10. Así, á 8 (á esquerda do 9) sumábaselle 1, sendo o número superior 9065.

Daquela (5 arriba) por (8 abaixo), calcular; escribir 0 no canto de 5 e engadir 4 ao 6 (á esquerda do 5) obtendo 10; escribir 0 en lugar do 6 e sumar 1 ao 0 (á esquerda do 6) paira obter 1. Aquí finalizaba o terceiro e último paso, sendo o número superior 9100. Isto era precisamente o produto. Una nota: cando nós escribimos 0 eles deixaron a columna baleira (figura 6).

Figura .

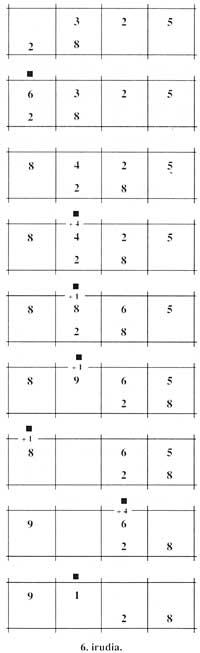
En resumo, podemos escribir:

Pero este método era longo e molesto. Cando atoparon o cero, deixaron de utilizar o ábaco e as cifras tomaron o valor segundo o lugar. Isto facilitou o cálculo das operacións aos matemáticos hindús.

Velaquí como se multiplicou a partir do século V. Trátase do chamado método de cuadrícula, ao que os europeos denominaron per gelosia (saretazko).

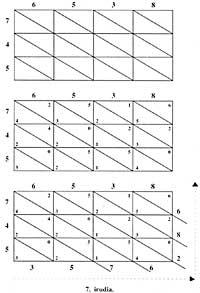
Supoñamos que queremos multiplicar 6358 x 547. Como o multiplicador 4 ten 3 cifras, debuxamos un rectángulo de 4 columnas e 3 filas. Os números escríbense na cabeceira das columnas e filas respectivamente. Dividimos cada casa por unha diagonal que une o vértice superior esquerdo co inferior dereito.

En cada una das casas, una vez multiplicados os números que hai nas columnas e nas cabezas da fila, sendo este produto menor de 100, escríbese a cifra do dez na metade inferior e a das unidades na metade superior; paira a falta de unidades e decenas escríbese 0. Fóra do rectángulo e partindo do vértice superior dereito, no noso caso desde o 6, súmanse os números situados entre as diagonais. Se una destas sumas parciais tivese dúas cifras, a decimal engadiríase á seguinte suma e só escribiriamos a das unidades. O resultado lese de esquerda a dereita e de abaixo a arriba (figura 7).

Figura .

División

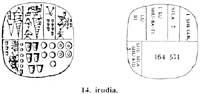
É sen beizos a operación máis complicada e inclúe todas as demais. Antes de explicar as divisións escritas, veremos una división de fai 46 séculos. De feito, hoxe no pobo de Fara de Iraq, pero no de C. O Shurupp de 2650 levou a cabo na cidade sumeria. Aínda que naquela época existían as cifras sumerianas, paira realizar as operacións utilizaban os antigos calculi. Lembremos como eran as calculi:

Figura .

Varias persoas repartiron un celeiro con 7 silas cebadas. Había que buscar o número de persoas e a cantidade de cebada sobrante. Un celeiro valía 1.152.000 silas. Por tanto, a operación a realizar era de 1.152.000 por 7. Mentres o cociente daríanos o número de persoas, a area daríanos a cebada sobrante.

Figura .

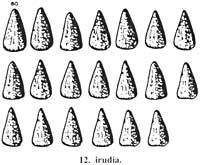
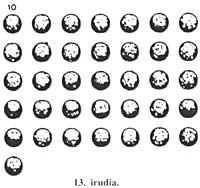
Paira representar 1.152.000 silas perforáronse 32 esferas. De feito 32 x 36.000 = 1.152.000. As esferas perforadas colocáronse en catro filas de 7 columnas (Figura 9), sobrando catro esferas perforadas. De aquí obtiveron 4 x 36.000 persoas e 4 x 36.000 en exceso de cebada. As catro esferas perforadas foron substituídas por 40 esferas (una esfera perforada tiña o valor de 10 esferas). As 40 esferas foron colocadas en cinco filas de sete columnas e 5 sobrantes de esfera (Figura 10).

Figura .
Así que 5 x 3600 máis e agora 5 x 3600 máis de cebada. A cambio de cinco esferas obtivéronse 30 grandes conos perforados (una esfera tiña o valor de 6 grandes conos perforados); 30 grandes conos perforados formaban catro filas de sete columnas e quedaban dous sobrantes. É dicir, tiñan 4 x 600 persoas máis e 2 x 600 silas sen repartir cebada (Figura 11). Os dous grandes conos perforados foron substituídos por 20 grandes conos (un cono grande perforado = dez conos grandes) que tamén se colocaron en dúas filas de 7 columnas, obtendo 2 x 60 máis e deixando 6 x 60 silas sen distribuír (Figura 12).
Figura .
Figura .
A cambio destas últimas tomáronse 36 bólas (un cono grande = seis bólas) e colocáronse en cinco filas de sete columnas, cunha bóla sobrante e 5 x 10 persoas máis (figura 13). Finalmente, substituíndo a bóla por dez conos e formando con eles una soa fila, é dicir, un amigo máis, e obtendo o resto final 3 silas cebadas (Figura 14). En resumo, 4 x 36.000 + 5 x 3.600 + 4 x 600 + 2 x 60 + 5 x 10 + 1 = 164.571 persoas e 3 silas cebadas. Una vez realizada a operación, o resultado escribíase nunha táboa con cifras (figura 15).
Figura .
Figura .
Figura .
En canto á división escrita, os egyptianos utilizaban un método similar ao utilizado na multiplicación. 1476 dividido por 12 divisións, coma se tratásese dunha multiplicación, 1 e 12 en dúas columnas e debaixo de cada una delas escribían dobres (figura 16), ata que na columna do 12 aparecía o maior dobre ou o mesmo número 1476. Entón na columna da dereita marcábanse os números que sumaban 1476 e sumaban os números da columna da esquerda aos que correspondían.
Figura .

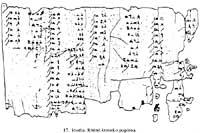
É dicir, 1476 : 12 = 64 + 32 + 16 + 8 + 2 + 1 = 123. Loxicamente, paira poder levar a cabo este tipo de división, a división debe ser exacta. Con todo, os egyptianos coñecían una laboriosa técnica de división inexacta. De feito, os egyptianos coñecían fraccións unitarias e utilizábanas paira calcular cocientes 2/n. No papiro Rhind (figura 17) aparece una táboa de descomposicións dos cocientes 2/n, sendo n impar e de 5 a 101.

Figura .
Figura .

Cambiando a tempo, o método utilizado en Europa antes de 1600 era o método de perda ou eliminación. A continuación, utilizando a división 1556 : 42, veremos en que consistía o método:

O éxito deste método débese á facilidade de uso no ábaco sobre area.

XV. No século XVIII créase un novo método de división chamado adanda. Coa palabra adanda (dando) significa, a súa causa está no propio algoritmo. De feito, cando se quita o produto parcial báixase a seguinte cifra e dáse á area. A continuación podemos ver un exemplo do algoritmo de adanda. Este método é, sen dúbida, o pioneiro de hoxe.

Babesleak
Eusko Jaurlaritzako Industria, Merkataritza eta Turismo Saila