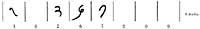Hasiera »   Erreportajeak »   Eragiketak nola? (II). Biderkaketa eta zatiketa

How to operate? (II). Multiplication and division

• Zabaldu:
• Twitter
• Facebook
• Emaila

As for multiplication, we must mention a particular case. In the manual product mentioned above, it was said that the fingers lowered in the hands multiplied by 10.

Multiplication Multiplication

As for multiplication, we must mention a special case (which has as a product the number 10). In the manual product mentioned above, it was said that the fingers lowering in the hands multiplied by 10 (mentally). Inside this head is: the number of fingers that go down gives us a tenth of the product.

The Egyptians also knew how to multiply by 10. After writing a number for it, each symbol of an order was replaced by a symbol of the following order (Figure 1).

In the Chinese numbering system you can also see the witness of this case. Depending on the place where the symbol 10 is placed, you can have two different meanings (figure 2): if you are placed to the left of the symbols of other smaller numbers, you have addition. If written to the right means multiplication.

Let's see how other multiplications were made.

The egypti wrote 1 and the smallest product on the top of two columns. Then these numbers were doubled consecutively and were written below. The doubles were made until column 1 obtained the other product (not the smallest) or, if it did not occur, until the number appeared larger than the other product. In the first case, the result would appear next to the other product, in the column on the right. In case a) of figure 3, the product 128 x 12 = 1536 is obtained. In the second case, in the left column (column 1) the numbers that added the largest product were selected. The result was obtained by adding in the column on the right the numbers corresponding to the previous numbers. In case b) of figure 3 appears the product 369 x 19 = 4864 + 1216 + 608 + 304 + 19 = 7011.

The Egyptian multiplication was, therefore, implea and did not need tables. But it was not the only method used by Egyptians. They also used the method called unfolding. On this occasion the two products were written on the head of two columns, calculating half of the largest (disregarding the remains) and double of the smallest and placing them in the corresponding columns. In the column of pairs were added the corresponding to the odd numbers of the column of means, obtaining the product. Figure 4 shows the product 54 x 37 = 74 + 148 + 592 + 1184 = 1998. This method also appears in some countries of the Soviet Union.

The Hindus used a column abacus in sand. In this abacus, in the column on the right, they wrote the units; when the dozens were on their left; the percentages on their left, etc. They were left blank to indicate the lack of units (Figure 5).

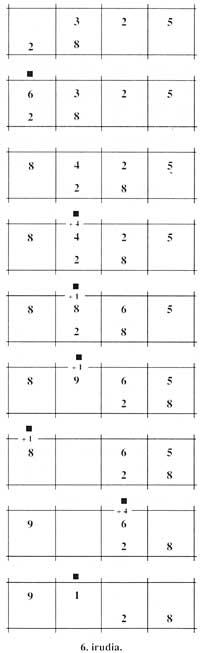
This abacus was used to perform multiplications. For example, to calculate the product 325 x 28 they were written in a four-column abacus, the largest in the upper right and the second in the lower left. In the first step, they calculated (3 above) by (2 below), 6 and wrote in the left column of 3. Then (3 above) by (8 below), 24, and instead of 3 they wrote 4 and added 2 to the previous 6.

The first step had already been completed. Before starting the second, the bottom number moved by a column to the right. Now (2 above) it was calculated by (2 below), 4, and was added to the previous 4 (left of the upper 2). Then (2 above) by (8 below), calculate and replace 2 by 6, eliminating 2 and adding 1 to 8 that was on your left. Thus ended the second step and a column with the bottom number to the right. In the third step (5) by (2 lower), calculate 10; added 0 and 6 (5 left) and 1 and 9 (6 left), being the first 6 and the second 10. Thus, at 8 (on the left of 9) it was added 1, being the upper number 9065.

Then (5 above) by (8 below), calculate; write 0 instead of 5 and add 4 to 6 (left of 5) getting 10; write 0 instead of 6 and add 1 to 0 (left of 6) to get 1. Here was the third and last step, being the top number 9100. This was precisely the product. A note: when we write 0 they left the column empty (figure 6).

In summary, we can write:

But this method was long and annoying. When they found zero, they stopped using the abacus and the figures took the value according to the place. This facilitated the calculation of operations to Hindu mathematicians.

Here is how it multiplied from the fifth century. This is the so-called grid method, which Europeans called per gelosia (saretazko).

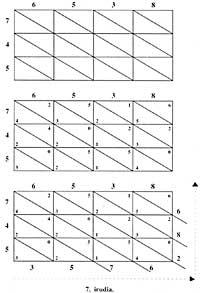
Suppose we want to multiply 6358 x 547. As the multiplier 4 has 3 figures, we draw a rectangle of 4 columns and 3 rows. The numbers are written in the header of the columns and rows respectively. We divide each square by a diagonal that joins the upper left vertex with the lower right.

In each of the squares, once multiplied the numbers that are in the columns and in the heads of the row, being this product less than 100, the number of the ten is written in the lower half and that of the units in the upper half; for the lack of units and dozens is written 0. Outside the rectangle and starting from the top right vertex, in our case since the 6, are added the numbers located between the diagonals. If one of these partial sums had two figures, the decimal would be added to the next sum and we would only write that of the units. The result is read from left to right and from bottom to top (figure 7).

Division Division

It is without lips the most complicated operation and includes all the others. Before explaining the written divisions, we will see a division of 46 centuries ago. In fact, today in the town of Fara of Iraq, but in that of C. The Shurupp of 2650 was held in the Sumerian city. Although at that time the Sumerian figures existed, to carry out the operations they used the old calculi. Remember how the calculi were:

Several people distributed a barn with 7 barley silas. We had to look for the number of people and the amount of surplus barley. A barn was worth 1,152,000 silas. Therefore, the operation to be carried out was 1,152,000 by 7. While the ratio would give us the number of people, the sand would give us the surplus barley.

To represent 1,152,000 silas, 32 spheres were perforated. In fact 32 x 36,000 = 1,152,000. The perforated spheres were placed in four rows of 7 columns (Figure 9), with four perforated spheres remaining. From here they obtained 4 x 36,000 people and 4 x 36,000 in excess of barley. The four perforated spheres were replaced by 40 spheres (a perforated sphere had the value of 10 spheres). The 40 spheres were placed in five rows of seven columns and 5 surplus sphere (Figure 10).

So 5 x 3600 more and now 5 x 3600 more barley. In exchange for five spheres, 30 large perforated cones were obtained (one sphere had the value of 6 large perforated cones); 30 large perforated cones formed four rows of seven columns and two leftovers remained. That is, they had 4 x 600 more people and 2 x 600 silas without cebada (Figure 11). The two large perforated cones were replaced by 20 large cones (a large perforated cone = ten large cones) which were also placed in two rows of 7 columns, obtaining 2 x 60 more and leaving 6 x 60 undistributed silas (Figure 12). In exchange for the latter, 36 balls were taken (a large cone = six balls) and placed in five rows of seven columns, with a surplus ball and 5 x 10 more people (figure 13). Finally, replacing the ball with ten cones and forming with them a single row, that is, one more friend, and getting the rest final 3 barley silas (Figure 14). In summary, 4 x 36,000 + 5 x 3,600 + 4 x 600 + 2 x 60 + 5 x 10 + 1 = 164,571 people and 3 barley silas. Once the operation was performed, the result was written in a table with figures (figure 15). As for written division, Egyptians used a method similar to that used in multiplication. 1476 divided by 12 divisions, as if it were a multiplication, 1 and 12 in two columns and under each of them wrote doubles (figure 16), until in the column of the 12 appeared the largest double or the same number 1476. Then in the column on the right were marked the numbers that totaled 1476 and added the numbers of the column on the left to which they corresponded.

That is, 1476 : 12 = 64 + 32 + 16 + 8 + 2 + 1 = 123. Logically, in order to carry out this type of division, the division must be accurate. However, the Egyptians knew a laborious technique of inaccurate division. In fact, Egyptians knew unitary fractions and used them to calculate quotients 2/n. In the papyrus Rhind (figure 17) appears a table of decompositions of the 2/n quotients, being n odd and from 5 to 101.

Changing in time, the method used in Europe before 1600 was the method of loss or elimination. Then using division 1556: 42, we will see what the method consisted of:

The success of this method is due to the ease of use in the abaco on sand.

XV. In the eighteenth century a new method of division called adanda was created. With the word adanda (giving) means, its cause is in the algorithm itself. In fact, when the partial product is removed, the following figure is lowered and given to the sand. Below we can see an example of the adanda algorithm. This method is, without a doubt, the pioneer of today.