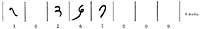¿Cómo operar? (II). Multiplicación y división
Multiplicación
En cuanto a la multiplicación, hay que mencionar un caso especial (que tiene como producto el número 10). En el producto manual mencionado anteriormente, se decía que los dedos que bajaban en las manos se multiplicaban por 10 (mentalmente). Dentro de este cabezal está: el número de dedos que bajan nos da la décima parte del producto.
Los egyptianos también sabían multiplicar por 10. Tras escribir un número para ello, cada símbolo de un orden era sustituido por un símbolo de orden siguiente (figura 1).

En el sistema de numeración chino también se puede ver el testigo de este caso. Dependiendo del lugar donde se ponga el símbolo 10, puede tener dos significados diferentes (figura 2): si se coloca a la izquierda de los símbolos de otros números más pequeños, se tiene suma. Si se escribe a la derecha significa multiplicación.

Veamos cómo se realizaban otras multiplicaciones.
Los egypti escribían 1 y el producto más pequeño en la parte superior de dos columnas. Luego se doblaban consecutivamente estos números y se escribían debajo. Los doblajes se hacían hasta que en la columna 1 se obtenía el otro producto (no el menor) o, si no ocurriera, hasta que apareciera el número más grande que el otro producto. En el primer caso aparecería el resultado junto al otro producto, en la columna de la derecha. En el caso a) de la figura 3 se obtiene el producto 128 x 12 = 1536. En el segundo caso, en la columna de la izquierda (columna 1) se seleccionaban los números que sumaban el mayor producto. El resultado se obtenía sumando en la columna de la derecha los números correspondientes a los números anteriores. En el caso b) de la figura 3 aparece el producto 369 x 19 = 4864 + 1216 + 608 + 304 + 19 = 7011.

La multiplicación egyptiana era, por tanto, implea y no necesitaba tablas. Pero no fue el único método utilizado por los egyptianos. También utilizaban el método denominado desdoblamiento. En esta ocasión los dos productos se escribían en la cabeza de dos columnas, calculando la mitad de la más grande (despreciando los restos) y las dobles de la más pequeña y colocándolas en las columnas correspondientes. En la columna de pares se sumaron los correspondientes a los números impares de la columna de medias, obteniendo el producto. En la figura 4 se puede ver el producto 54 x 37 = 74 + 148 + 592 + 1184 = 1998. Este método también aparece en algunos países de la Unión Soviética.

Los hindúes usaban un ábaco de columna en arena. En este ábaco, en la columna de la derecha, escribían las unidades; cuando estaba a su izquierda las decenas; los porcentajes a su izquierda, etc. Dejaban en blanco para indicar la falta de unidades (figura 5).
Este ábaco se utilizaba para realizar las multiplicaciones. Por ejemplo, para calcular el producto 325 x 28 se escribían en un ábaco de cuatro columnas, el mayor en la parte superior derecha y el segundo en la parte inferior izquierda. En el primer paso, calculaban (3 arriba) por (2 abajo), 6 y escribían en la columna izquierda del 3. A continuación (3 arriba) por (8 abajo), 24, y en vez de 3 escribían 4 y añadían 2 al 6 anterior.
El primer paso ya había finalizado. Antes de comenzar el segundo, el número inferior se movía por una columna hacia la derecha. Ahora (2 arriba) se calculaba por (2 abajo), 4, y se añadía a la 4 anterior (a la izquierda de la 2 superior). Luego (2 arriba) por (8 abajo), calcular y sustituir el 2 por 6, eliminando el 2 y sumar 1 al 8 que estaba a su izquierda. Así acababa el segundo paso y una columna con el número inferior hacia la derecha. En el tercer paso (5) por (2 inferior), calcular 10; se sumaban 0 y 6 (5 izquierda) y 1 y 9 (6 izquierda), siendo el primero 6 y el segundo 10. Así, a la 8 (a la izquierda del 9) se le sumaba 1, siendo el número superior 9065.
Luego (5 arriba) por (8 abajo), calcular; escribir 0 en vez de 5 y añadir 4 al 6 (a la izquierda del 5) obteniendo 10; escribir 0 en lugar del 6 y sumar 1 al 0 (a la izquierda del 6) para obtener 1. Aquí finalizaba el tercer y último paso, siendo el número superior 9100. Esto era precisamente el producto. Una nota: cuando nosotros escribimos 0 ellos dejaron la columna vacía (figura 6).
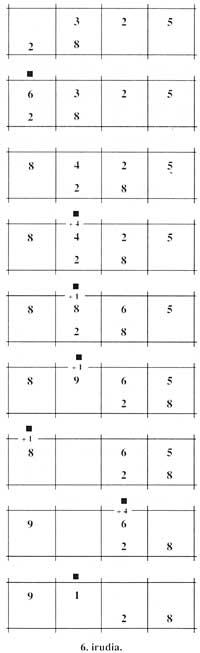
En resumen, podemos escribir:

Pero este método era largo y molesto. Cuando encontraron el cero, dejaron de utilizar el ábaco y las cifras tomaron el valor según el lugar. Esto facilitó el cálculo de las operaciones a los matemáticos hindúes.
He aquí cómo se multiplicó a partir del siglo V. Se trata del llamado método de cuadrícula, al que los europeos denominaron per gelosia (saretazko).
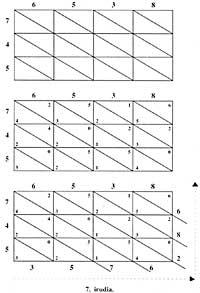
Supongamos que queremos multiplicar 6358 x 547. Como el multiplicador 4 tiene 3 cifras, dibujamos un rectángulo de 4 columnas y 3 filas. Los números se escriben en la cabecera de las columnas y filas respectivamente. Dividimos cada casilla por una diagonal que une el vértice superior izquierdo con el inferior derecho.
En cada una de las casillas, una vez multiplicados los números que hay en las columnas y en las cabezas de la fila, siendo este producto menor de 100, se escribe la cifra de las diez en la mitad inferior y la de las unidades en la mitad superior; para la falta de unidades y decenas se escribe 0. Fuera del rectángulo y partiendo del vértice superior derecho, en nuestro caso desde el 6, se suman los números situados entre las diagonales. Si una de estas sumas parciales tuviese dos cifras, la decimal se añadiría a la siguiente suma y sólo escribiríamos la de las unidades. El resultado se lee de izquierda a derecha y de abajo a arriba (figura 7).
División
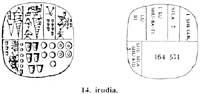
Es sin labios la operación más complicada e incluye todas las demás. Antes de explicar las divisiones escritas, veremos una división de hace 46 siglos. De hecho, hoy en el pueblo de Fara de Irak, pero en el de C. El Shurupp de 2650 se llevó a cabo en la ciudad sumeria. Aunque en aquella época existían las cifras sumerianas, para realizar las operaciones utilizaban los antiguos calculi. Recordemos cómo eran las calculi:
Varias personas repartieron un granero con 7 silas cebadas. Había que buscar el número de personas y la cantidad de cebada sobrante. Un granero valía 1.152.000 silas. Por tanto, la operación a realizar era de 1.152.000 por 7. Mientras el cociente nos daría el número de personas, la arena nos daría la cebada sobrante.

Para representar 1.152.000 silas se perforaron 32 esferas. De hecho 32 x 36.000 = 1.152.000. Las esferas perforadas se colocaron en cuatro filas de 7 columnas (Figura 9), sobrando cuatro esferas perforadas. De aquí obtuvieron 4 x 36.000 personas y 4 x 36.000 en exceso de cebada. Las cuatro esferas perforadas fueron sustituidas por 40 esferas (una esfera perforada tenía el valor de 10 esferas). Las 40 esferas fueron colocadas en cinco filas de siete columnas y 5 sobrantes de esfera (Figura 10).




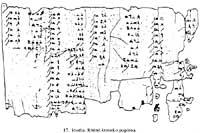
Es decir, 1476 : 12 = 64 + 32 + 16 + 8 + 2 + 1 = 123. Lógicamente, para poder llevar a cabo este tipo de división, la división debe ser exacta. Sin embargo, los egyptianos conocían una laboriosa técnica de división inexacta. De hecho, los egyptianos conocían fracciones unitarias y las utilizaban para calcular cocientes 2/n. En el papiro Rhind (figura 17) aparece una tabla de descomposiciones de los cocientes 2/n, siendo n impar y de 5 a 101.

Cambiando a tiempo, el método utilizado en Europa antes de 1600 era el método de pérdida o eliminación. A continuación, utilizando la división 1556 : 42, veremos en qué consistía el método:
El éxito de este método se debe a la facilidad de uso en el ábaco sobre arena.
XV. En el siglo XVIII se crea un nuevo método de división llamado adanda. Con la palabra adanda (dando) significa, su causa está en el propio algoritmo. De hecho, cuando se quita el producto parcial se baja la siguiente cifra y se da a la arena. A continuación podemos ver un ejemplo del algoritmo de adanda. Este método es, sin duda, el pionero de hoy.