Diagramas lóxicos (I)
Ao longo da historia das matemáticas as imaxes resultaron moi útiles paira os matemáticos. A partir dos números representáronse rectas, planos, espazo, elipses, circunferencias, conos, paraboloides, funciones seo e coseno, exponenciais, funcións de dúas, tres e catro variables, funcións complexas e mil cosas máis que existen no mundo das matemáticas. É máis, utilizáronse tanto paira representar as cousas como paira demostrar algunhas propiedades, temóns e teoremas.
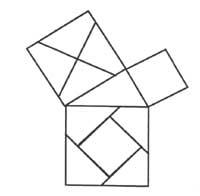
A modo de exemplo, citariamos algúns casos: O noso mito, lenda ou historia sobre a morte de Arquímedes. a.C. No ano 212, cando os soldados eromáticos tomaron con armas a cidade de Siracusa, cando Arquímedes formaba parte dunha demostración xeométrica, foi asasinado por unha espada. (Hai que lembrar que naquela época as imaxes facíanse en area). Pero sen ser tan tráxico, aí está a demostración a través de imaxes do teorema de Pitágoras (Figura 1). Por último M. Trátase dun artigo do mestre Willians no que, coa axuda do tangram, aparecen algunhas probas matemáticas de Euklides.
Pero nesta liña os matemáticos foron máis lonxe e non se quedaron nas representacións destes conceptos tan coñecidos. A súa valentía foi máis aló e chegaron a imaxinar a linguaxe, a idea, o propio razoamento. Por lóxica, as matemáticas e a filosofía únense. Neste artigo falaremos da representación da lóxica.
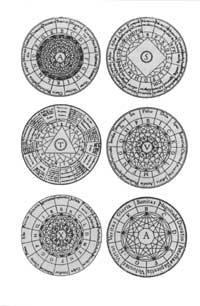
Uno dos pioneiros na representación dos razoamentos é o catalán Ramón Llull. Na súa obra mestra Ars Magna quixo explicar calquera tema mediante sistemas de círculos concéntricos. Entre outras (figura 2), Deus (A,A) e a calidade da alma (S), a relación entre as cousas (T), sete virtudes e sete pecados (V) ou mentira e verdade (X). Llull conseguía todas as combinacións posibles movendo círculos.
Tras esta mención especial e esquecendo a outros pioneiros, imos describir o primeiro sistema utilizado na historia da análise da lóxica. Este é só o diagrama de Venn. Os diagramas de Venn utilizáronse na teoría de conxuntos que, dentro da matemática moderna, é un tema básico. Ademais, serviu paira resolver os problemas da lóxica clásica herdada de Aristóteles grego e do concepto de silogismo.
Sen dúbida, a aparición da definición de algebra de clase de Boole tivo una gran influencia no éxito obtido polos diagramas de Venn.
Comecemos por aplicar as regras básicas paira un bo funcionamento dos diagramas:
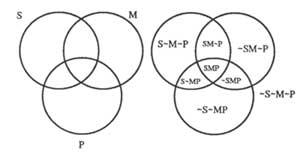
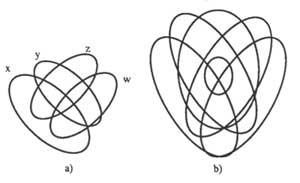
– Cada un dos círculos representará una clase; os puntos dentro do círculo serán clases e os exteriores serán de clase non. Se a clase é S paira non S escribimos &S. A figura 3 mostra un diagrama de tres clases.
– Paira indicar que non hai elementos nunha clase, escureceremos. Indicaremos que hai algún elemento cunha X. Se os elementos poden estar en dúas zonas contiguas, anotaremos X no límite.
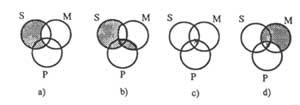
Na figura 4 pódense ver os seguintes diagramas de premisas
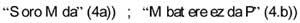
Do diagrama 4b) dedúcese que: “Ningunha S é P”.
“Hai S M” (4c) (X está no límite porque non sabemos onde están os elementos nun, outro ou ambos os).
Se a segunda premisa fóra “M ouro P é”, deberiamos escribir en X medio: 4d).
Cando aparecen máis de tres temas complícase. Os círculos deben ser substituídos por elipses, 5 a) e en ocasións por imaxes non conectadas 5b).
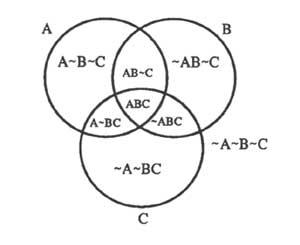
Tamén se pode utilizar no cálculo de proposta creado como interpretación do cálculo de clases. Paira iso é necesario modificar as normas ditadas e darlle una nova interpretación. Agora os círculos representan as propostas. Estas poden ser certas ou falsas. Antes escureciamos as rexións sen elementos. Agora tamén se escurecen paira expresar combinacións imposibles dos valores. A figura 6 mostra catro círculos: grandes (A, B e C) correspondentes ás proposicións e pequenos (non A nin B nin C, &A B&&C) paira indicar a cara exterior das proposicións A, B e C e facilitar a escuridade.
Na figura 7 pódense ver algúns exemplos:
7a) “A é certa”; 7b) “A é falsa” (ou “&A é certa”).
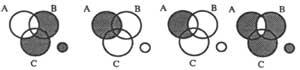
O diagrama condicional “Si A é certo B é certo”, escríbese A … B. O plan obxecto desta relación é CE, EF, FE e FF (Verdadeiro, Falso), dos cales só EF non é válido. Por tanto, as rexións coa&B (A, non B) deben escurecerse como se observa no diagrama 7 c), é dicir, o diagrama correspondente á proposta “A ouro B dá”. Si á proposta anterior engadimos a proposición “A é certa”, é dicir, escurecemos &A, obteremos o diagrama da figura 7d) e como conclusión obtemos “B é verdadeiro”.
Na figura 7b) pódese observar que a falsidade A non implica que a B sexa falsa ou certa, podendo ser una ou outra. Pola contra, na figura 7d) obsérvase que o feito de que A sexa certa debe ser necesariamente certo.
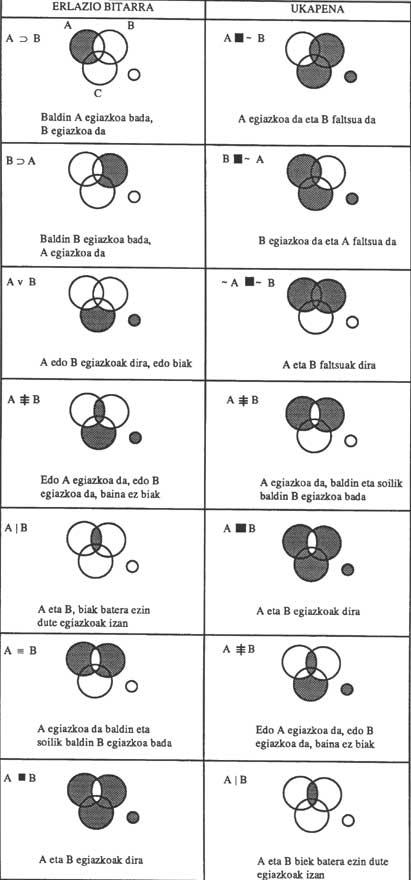
A figura 8 mostra os diagramas de todas as relacións binarias entre os termos A e B, así como das súas denegacións. Se se inclúe o terceiro tema C, o diagrama é facilmente extensible aos tres temas. Antes explicaremos a redacción:

De momento deixaremos aquí a descrición dos Diagramas Lóxicos. No seguinte número, Elhuyar. No número 26 de Ciencia e Técnica (setembro) preténdese publicar a segunda e última parte do artigo, dando por finalizada a descrición completa do tema.