Diagrammes logiques (I)
Tout au long de l'histoire des mathématiques images ont été très utiles pour les mathématiciens. Des nombres ont été représentés droites, plans, espace, ellipses, circonférences, cônes, paraboles, sinus et cosinus fonctions, exponentielles, fonctions de deux, trois et quatre variables, fonctions complexes et mille autres choses qui existent dans le monde des mathématiques. En outre, ils ont été utilisés à la fois pour représenter les choses et de démontrer certaines propriétés, des gouvernails et des théorèmes.
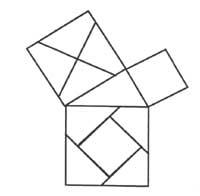
A titre d'exemple, nous citerons quelques cas : Notre mythe, légende ou histoire sur la mort d'Archimède. a.C. En 212, quand les soldats eromatiques prirent avec des armes la ville de Syracuse, quand Archimède faisait partie d'une démonstration géométrique, il fut tué par une épée. (Il faut se rappeler qu'à cette époque les images étaient faites en sable). Mais sans être si tragique, voici la démonstration à travers des images du théorème de Pythagore (Figure 1). Enfin M. Il s'agit d'un article du maître Willians dans lequel, avec l'aide du tangram, apparaissent quelques preuves mathématiques d'Euklides.
Mais dans cette ligne, les mathématiciens sont allés plus loin et ne sont pas restés dans les représentations de ces concepts bien connus. Leur courage est allé plus loin et ils sont venus à imaginer le langage, l'idée, le raisonnement lui-même. Par logique, les mathématiques et la philosophie sont réunis. Dans cet article, nous parlerons de la représentation de la logique.
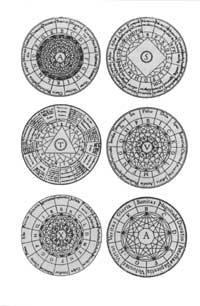
Un des pionniers dans la représentation des raisonnements est le catalan Ramón Llull. Dans son chef-d'œuvre Ars Magna, il a voulu expliquer n'importe quel sujet par des systèmes de cercles concentriques. Entre autres (figure 2), Dieu (A,A) et la qualité de l'âme (S), la relation entre les choses (T), sept vertus et sept péchés (V) ou mensonge et vérité (X). Lulle obtenait toutes les combinaisons possibles en déplaçant des cercles.
Après cette mention spéciale et oubliant d'autres pionniers, nous allons décrire le premier système utilisé dans l'histoire de l'analyse de la logique. Ce n'est que le diagramme de Venn. Les diagrammes de Venn ont été utilisés dans la théorie des ensembles qui, dans les mathématiques modernes, est un sujet de base. En outre, il a servi à résoudre les problèmes de la logique classique héritée d'Aristote grec et du concept de syllogisme.
Sans doute, l'apparition de la définition algèbre de classe de Boole a eu une grande influence sur le succès obtenu par les diagrammes de Venn.
Commençons par appliquer les règles de base pour un bon fonctionnement des diagrammes:
– Chacun des cercles représentera une classe; les points à l’intérieur du cercle seront des classes et les extérieurs seront de classe non. Si la classe est S pour non S nous écrivons &S. La figure 3 montre un diagramme de trois classes.
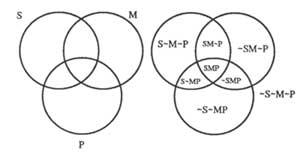
– Pour indiquer qu’il n’y a pas d’éléments dans une classe, nous obscurcissons. Nous indiquerons qu'il y a un élément avec un X. Si les éléments peuvent être dans deux zones contiguës, nous marquerons X à la limite.
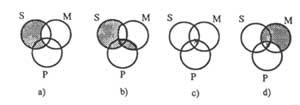
La figure 4 montre les diagrammes de prémisses suivants
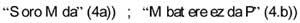
Du diagramme 4b) on déduit que : “Aucun S est P”.
«Il y a S M» (4c) (X est à la limite parce que nous ne savons pas où sont les éléments dans un, un autre ou les deux).
Si la deuxième prémisse était “M oro P es”, nous devrions écrire en X moyen: 4d).
Lorsque plus de trois thèmes apparaissent, il devient compliqué. Les cercles doivent être remplacés par des ellipses, 5 a) et parfois par des images non connectées 5b).
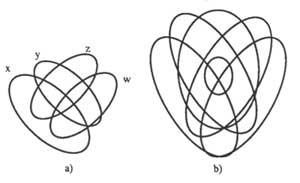
Il peut également être utilisé dans le calcul de proposition créé comme interprétation du calcul des classes. Pour cela, vous devez modifier les règles dictées et lui donner une nouvelle interprétation. Maintenant, les cercles représentent les propositions. Elles peuvent être vraies ou fausses. Auparavant, nous obscurcissons les régions sans éléments. Maintenant, ils sont également obscurcis pour exprimer des combinaisons impossibles de valeurs. La figure 6 montre quatre cercles : grands (A, B et C) correspondant aux propositions et petits (non A ni B ni C, & C) pour indiquer la face extérieure des propositions A, B et C et faciliter l'obscurité.
Dans la figure 7, vous pouvez voir quelques exemples:
7a) “A est vrai”; 7b) “A est faux” (ou “ A est vrai”).
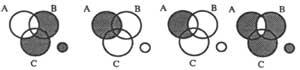
Le diagramme conditionnel “Si A est vrai B est vrai”, écrit A … B. Le plan objet de cette relation est CE, EF, FE et FF (Vrai, Faux), dont seulement EF n'est pas valide. Par conséquent, les régions où l’on trouve A et non B doivent être obscurcies comme le montre le diagramme 7 c), c’est-à-dire le diagramme correspondant à la proposition “A oro B da”. Si nous ajoutons à la proposition précédente la proposition “A est certaine”, c'est-à-dire que nous obscurcissons &A, nous obtiendrons le diagramme de la figure 7d) et en conclusion nous obtenons “B est vrai”.
Dans la figure 7b) on peut observer que la fausseté A n'implique pas que la B soit fausse ou certaine, pouvant être l'une ou l'autre. Au contraire, la figure 7d) montre que le fait que A est vrai doit nécessairement être vrai.
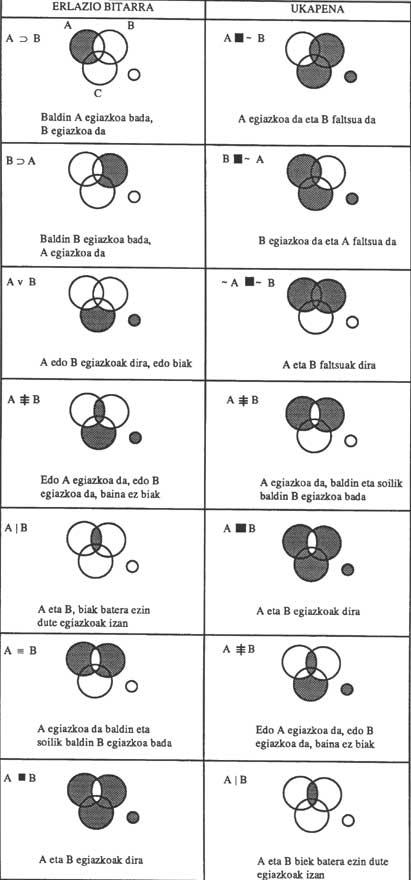
La figure 8 montre les diagrammes de toutes les relations binaires entre les termes A et B, ainsi que leurs refus. Si le troisième thème C est inclus, le diagramme est facilement extensible aux trois thèmes. Avant nous expliquerons la rédaction :

Pour l'instant nous laisserons ici la description des Diagrammes Logiques. Dans le prochain numéro, Elhuyar. Dans le numéro 26 de Science et Technique (septembre), on entend publier la deuxième et dernière partie de l'article, en mettant fin à la description complète du sujet.