Diagramas lógicos (I)
A lo largo de la historia de las matemáticas las imágenes han resultado muy útiles para los matemáticos. A partir de los números se han representado rectas, planos, espacio, elipses, circunferencias, conos, paraboloides, funciones seno y coseno, exponenciales, funciones de dos, tres y cuatro variables, funciones complejas y mil cosas más que existen en el mundo de las matemáticas. Es más, se han utilizado tanto para representar las cosas como para demostrar algunas propiedades, timones y teoremas.
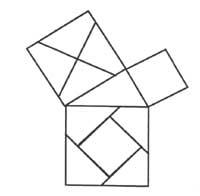
A modo de ejemplo, citaríamos algunos casos: Nuestro mito, leyenda o historia sobre la muerte de Arquímedes. a.C. En el año 212, cuando los soldados eromáticos tomaron con armas la ciudad de Siracusa, cuando Arquímedes formaba parte de una demostración geométrica, fue asesinado por una espada. (Hay que recordar que en aquella época las imágenes se hacían en arena). Pero sin ser tan trágico, ahí está la demostración a través de imágenes del teorema de Pitágoras (Figura 1). Por último M. Se trata de un artículo del maestro Willians en el que, con la ayuda del tangram, aparecen algunas pruebas matemáticas de Euklides.
Pero en esta línea los matemáticos han ido más lejos y no se han quedado en las representaciones de estos conceptos tan conocidos. Su valentía ha ido más allá y han llegado a imaginar el lenguaje, la idea, el propio razonamiento. Por lógica, las matemáticas y la filosofía se unen. En este artículo hablaremos de la representación de la lógica.
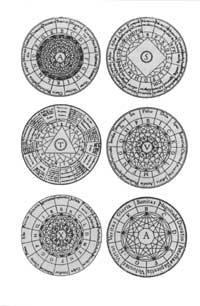
Uno de los pioneros en la representación de los razonamientos es el catalán Ramón Llull. En su obra maestra Ars Magna quiso explicar cualquier tema mediante sistemas de círculos concéntricos. Entre otras (figura 2), Dios (A,A) y la cualidad del alma (S), la relación entre las cosas (T), siete virtudes y siete pecados (V) o mentira y verdad (X). Llull conseguía todas las combinaciones posibles moviendo círculos.
Tras esta mención especial y olvidando a otros pioneros, vamos a describir el primer sistema utilizado en la historia del análisis de la lógica. Este es sólo el diagrama de Venn. Los diagramas de Venn se han utilizado en la teoría de conjuntos que, dentro de la matemática moderna, es un tema básico. Además, ha servido para resolver los problemas de la lógica clásica heredada de Aristóteles griego y del concepto de silogismo.
Sin duda, la aparición de la definición de algebra de clase de Boole tuvo una gran influencia en el éxito obtenido por los diagramas de Venn.
Comencemos por aplicar las reglas básicas para un buen funcionamiento de los diagramas:
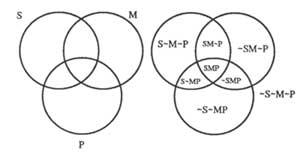
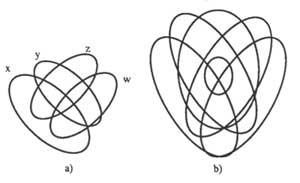
– Cada uno de los círculos representará una clase; los puntos dentro del círculo serán clases y los exteriores serán de clase no. Si la clase es S para no S escribimos &S. La figura 3 muestra un diagrama de tres clases.
– Para indicar que no hay elementos en una clase, oscureceremos. Indicaremos que hay algún elemento con una X. Si los elementos pueden estar en dos zonas contiguas, anotaremos X en el límite.
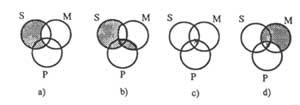
En la figura 4 se pueden ver los siguientes diagramas de premisas
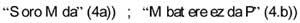
Del diagrama 4b) se deduce que: “Ninguna S es P”.
“Hay S M” (4c) (X está en el límite porque no sabemos dónde están los elementos en uno, otro o ambos).
Si la segunda premisa fuera “M oro P es”, deberíamos escribir en X medio: 4d).
Cuando aparecen más de tres temas se complica. Los círculos deben ser sustituidos por elipses, 5 a) y en ocasiones por imágenes no conectadas 5b).
También se puede utilizar en el cálculo de propuesta creado como interpretación del cálculo de clases. Para ello es necesario modificar las normas dictadas y darle una nueva interpretación. Ahora los círculos representan las propuestas. Estas pueden ser ciertas o falsas. Antes oscurecíamos las regiones sin elementos. Ahora también se oscurecen para expresar combinaciones imposibles de los valores. La figura 6 muestra cuatro círculos: grandes (A, B y C) correspondientes a las proposiciones y pequeños (no A ni B ni C, &A&B&C) para indicar la cara exterior de las proposiciones A, B y C y facilitar la oscuridad.
En la figura 7 se pueden ver algunos ejemplos:
7a) “A es cierta”; 7b) “A es falsa” (o “&A es cierta”).
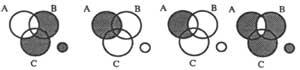
El diagrama condicional “Si A es cierto B es cierto”, se escribe A … B. El plan objeto de esta relación es CE, EF, FE y FF (Verdadero, Falso), de los cuales sólo EF no es válido. Por tanto, las regiones con A&B (A, no B) deben oscurecerse como se observa en el diagrama 7 c), es decir, el diagrama correspondiente a la propuesta “A oro B da”. Si a la propuesta anterior añadimos la proposición “A es cierta”, es decir, oscurecemos &A, obtendremos el diagrama de la figura 7d) y como conclusión obtenemos “B es verdadero”.
En la figura 7b) se puede observar que la falsedad A no implica que la B sea falsa o cierta, pudiendo ser una u otra. Por el contrario, en la figura 7d) se observa que el hecho de que A sea cierta debe ser necesariamente cierto.
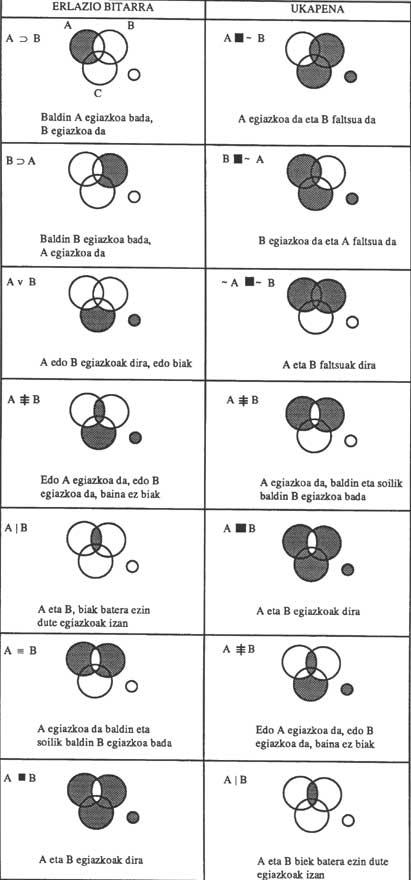
La figura 8 muestra los diagramas de todas las relaciones binarias entre los términos A y B, así como de sus denegaciones. Si se incluye el tercer tema C, el diagrama es fácilmente extensible a los tres temas. Antes explicaremos la redacción:

De momento dejaremos aquí la descripción de los Diagramas Lógicos. En el siguiente número, Elhuyar. En el número 26 de Ciencia y Técnica (septiembre) se pretende publicar la segunda y última parte del artículo, dando por finalizada la descripción completa del tema.