Le problème des entrepôts

Publicis achète chaque exemplaire de journal à 0,50 livres et le vend en 1 livre. Cependant, les exemplaires qui lui restent non vendus, le lendemain le grossiste les achète à 0,20 livres par unité. Ce système de vente semble aussi familier ou cruel, mais la société qui s'occupe de la vente en gros dépend également de la cruauté de l'imprimeur, qui à son tour dépend des fournisseurs, (et un long etc.). Tout cela est une histoire cruelle, l'histoire de notre cadre économique.
Pour Publicis les jours heureux sont seulement occasionnels et souvent vous n'avez pas la possibilité de compenser vos dettes. La faim est un mauvais conseiller, mais qui sait? Il peut nous guider vers la connaissance et l'analyse statistique.
Le lendemain d'une difficile journée de travail, il a passé une première grande étape pour connaître sa trajectoire vitale et a décidé de faire un bilan de son activité. Selon les données quotidiennes, il n'a jamais vendu 50 unités le même jour. Il a atteint un maximum de 40 unités. D'autre part, il vendait souvent 30 unités et vendait plus souvent 20 unités. Logiquement, ce chiffre d'affaires est dû à des faits politiques ou des nouvelles apparues sur la première page.
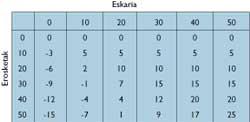
Quand on devient un homme d'affaires il devient comptable (certains voudraient que l'affirmation contraire soit certaine). C'est pourquoi notre héros a préparé une table avec des avantages.
Publicis est étonné en consultant la table. Par exemple : Acheter 50 unités peut gagner 25 livres, mais risque 15 livres.
La capacité dans les affaires est presque toujours liée à la perception de l'avenir. Inquiet, notre ami est sûr que vous devez analyser le problème de près. En conséquence, le diable de la statistique est entré dans son esprit, qui, d'autre part, est assez mal préparé à accepter un locataire si insupportable. Voici ses réflexions:
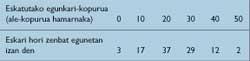
L'important n'est pas ce que je gagne un jour, mais ce que je peux gagner en un mois ou deux mois ou plus. Est-il impossible de prévoir ce que je peux gagner annuellement si j'achetais le même nombre de journaux chaque jour ? Mais combien devrait être ce montant? Et comment connaître le comportement des clients ? Eh bien, après une saison, après la vente du lot quotidien, au lieu d'abandonner, je resterai comme si je n'avais pas terminé le travail jusqu'à sept heures. Ainsi, en plus des ventes, je peux aussi marquer les demandes que j'ai et que je ne peux pas servir. Si je n'ai pas d'unités à vendre, je dois juste demander des excuses aux clients. Eh bien, pour bien faire les choses et pour arrondir les chiffres, je verrai ce qui se passe en 100 jours.
Nous reconnaissons que notre vendeur de journaux a toutes les caractéristiques pour devenir millionnaire. En conséquence, Publicis a trouvé les données du tableau 2:
Pensons — dit-on — que l'avenir ressemble au passé. Il serait intéressant de calculer ce qui se passerait si j'achetais quotidiennement le même nombre d'unités, les quantités 0, 10, 20, ..., 50. Dans ces conditions, en utilisant mon tableau de fréquence, je pourrais calculer le rendement total de 100 jours. Grâce à cela, en divisant par 100, je bénéficierais chaque jour. Par conséquent, en tenant compte des tableaux 1 et 2, on peut calculer le tableau 3 des rendements moyens.
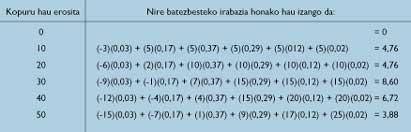
Le lecteur peut surprendre en découvrant qu'un pauvre vendeur de journaux trouve les principes de base de probabilité et de statistique. Pourquoi ne peut pas être rapide et habile? L'ensemble des marchands de journaux aura à voir avec celui des gens rapide et compétent.
Par conséquent, si j'achète 30 journaux par jour mon rendement moyen journalier sera de 8,60 livres, a conclu Publicis en regardant la table 3.
Ainsi se réinvente la moyenne mathématique, l'amélioration d'une fonction économique et l'avenir économique.
Mais notre histoire n'est pas encore terminée.
Un ami de Publicis était un étudiant en mathématiques qui aimait être jeune, être bon et discuter. À 20 ans, au lieu de parler du temps, du futur ou du passé, il préférait parler de quelque chose de plus technique dans ses exposés. Ainsi naquit la collaboration entre l'Université et le commerce.
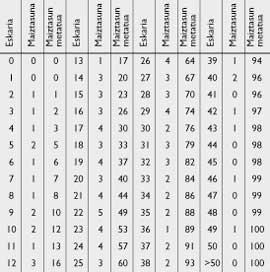
Notre jeune mathématicien voulait trouver la formule confortable qu'il pouvait utiliser son ami. Une fois réunis dans un petit bar et grâce aux données exactes prises par Publicis (voir tableau 4), il a pu faire une déclaration plus élaborée pour faciliter son utilisation. De la fréquence des ventes, l'ami de Publicis a calculé la courbe de fréquence accumulée qui apparaît dans la figure 1.
Le vendeur se demandait quel rôle il allait jouer dans son problème.
La notion de probabilité, comme nous le comprenons, n'a pas fait l'objet de travaux mathématiques jusqu'à il ya environ 300 ans. Cependant, dans ces êtres, il y a un concept indéterminé de « chance ».
Écoutons une interview entre nos deux amis qui sont à la table du bar:
Si l'avenir se répète avec la même fréquence indiquée par le passé, dit l'étudiant, vous avez 12 chances de vendre un maximum de 10 journaux de 100 jours, un maximum de 13 journaux, ..., 44 chances de vendre un maximum de 21, (voir tableau 4)
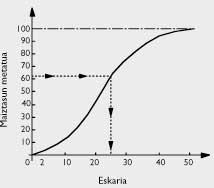
Nous utiliserons P(x) au maximum pour exprimer la probabilité de vendre x journaux. Souvent, grâce à un raisonnement très simple avec le nom de calcul marginal, vous découvrirez son rendement marginal et, ainsi, combien de journaux vous devrez acheter systématiquement dans les 100 prochains jours, toujours avec des fréquences passées à l'avenir.
Pensons que chaque jour vous achetez s-1 journaux. Que se passerait-il si vous décidez d'acheter un exemplaire ? Il gagnerait 0,50 livres avec probabilité 1-P(s-1) et perdrait 0,30 livres avec probabilité P(s-1). Donc, performance de remplissage:
serait 0,50 (1 - P(s-1)) - 0,30 P(s-1) ou 0,5 - 0,8 P(s-1).
Il est donc intéressant d'acheter un journal de plus si entre
0,5 et 0,8 P(s-1) 0 c'est-à-dire, P(s-1) 0,625
si elle est remplie. Mais quand P(s-1) est 0,625 vous ne vous intéressez pas.
Par conséquent, le nombre de journaux que vous devez acheter (afin que vous puissiez obtenir le meilleur rendement) sera celui qui répond à la condition P(s-1) 0.625 P(s).
Consulter le tableau 4:
s=26 étant P(25)=0,60 et P(26)=0,64.
Par conséquent, le meilleur inventaire sera s = 26.
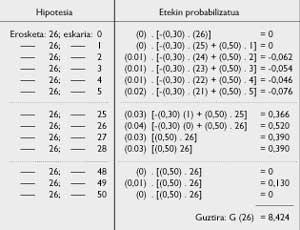
Mais quel sera le rendement moyen correspondant à l'inventaire s = 26 ? Les hypothèses de calcul et toutes les probabilités associées doivent être analysées. Si G(26) est un rendement moyen, vous obtenez le tableau 5.
De plus, on peut calculer le rendement moyen G(s) s'il s'agit d'un inventaire s en utilisant la formule de récurrence suivante:
G (s) = G (s-1) + 0,5 - 0,80 P (s-1)
Comme G(0) = 0 vous obtenez:
G(1) = 0,50 - (0,80)(0) = 0,50 G(2)
= 0,50 + 0,50 - (0,80)(0) = 1 G(3)
= 1+0,50 - (0,80)
= 1,492 G(4) = 1,492 + 0,50 - (0,80)
= 0,02) = 1,976 G(5) = 1,976 + 0,80
et ainsi de suite.
G(26) = 8,424; G(27) = 8,376, etc.

Un bon conseil – a conclu le jeune étudiant – est d'acheter chaque jour 26 journaux. Ainsi vous gagnerez le maximum moyen, c'est-à-dire 8,43 livres par jour. Dans tous les cas, cette décision doit être supprimée les jours spéciaux. Par exemple: dates de lancement de satellites (si vous pensez que vous êtes intéressé par vos clients), date d'annonce de baisse des impôts, etc. Mes conseils pour ces jours ne sont pas valables.
Comme vous le voyez, le commerce est toujours un mensonge. Cependant, puisque les événements spéciaux sont ainsi, adaptez votre commerce et votre vie aux données et aux jours normaux, qui sont plus nombreux. Oui, si vous ressentez un désir de stimuler et de développer les ventes, les mathématiques peuvent encore vous donner une petite aide, mais nous en parlerons dans un autre. Kaufman et R. Extrait du livre “Invitation à la recherche opérationnelle” de Faure.





