El problema de los almacenes

Publicis compra cada ejemplar de periódico en 0,50 libras y lo vende en 1 liberal. Sin embargo, los ejemplares que le quedan sin vender, al día siguiente los compra el mayorista en 0,20 libras por unidad. Este sistema de venta parece también coloquial o cruel, pero la sociedad que se encarga de la venta al por mayor también depende de la crueldad del impresor, que a su vez depende de los proveedores, (y un largo etcétera). Todo esto es una historia cruel, la historia de nuestro marco económico.
Para Publicis los días felices son sólo ocasionales y muchas veces no tiene la posibilidad de compensar sus deudas. El hambre es un mal asesor, pero ¿quién sabe? Puede que nos guíe al conocimiento y al análisis estadístico.
Al día siguiente de un difícil día de trabajo, pasó una primera gran etapa para conocer su trayectoria vital y decidió hacer un balance de su actividad. Según datos diarios, nunca llegó a vender 50 unidades el mismo día. Alcanzó un máximo de 40 unidades. Por otro lado, con frecuencia vendía 30 unidades y con más frecuencia llegaba a vender 20 unidades. Lógicamente, esta cifra de ventas se debió a hechos políticos o noticias aparecidas en la primera página.
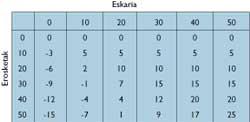
Al llegar uno a ser hombre de negocios se convierte en contador (algunos desearían que la afirmación contraria fuera cierta). Por eso, nuestro héroe ha preparado una tabla con beneficios.
Publicis se sorprende consultando la tabla. Por ejemplo: Comprando 50 unidades puede ganar 25 libras, pero arriesga 15 libras.
La habilidad en los negocios está casi siempre relacionada con la percepción del futuro. Preocupado, nuestro amigo está seguro de que tiene que analizar el problema de cerca. En consecuencia, el diablo de la estadística ha entrado en su mente, que, por otra parte, está bastante mal preparado para aceptar a un inquilino tan insoportable. A continuación se resumen sus reflexiones:
Lo importante no es lo que gano un día, sino lo que puedo ganar en un mes o dos meses o más. ¿No es posible prever lo que puedo ganar anualmente si comprara el mismo número de periódicos cada día? Pero, ¿cuánto debería ser esa cantidad? ¿Y cómo conocer el comportamiento de los clientes? Bueno, después de una temporada, una vez finalizada la venta del lote diario, en lugar de abandonar, me quedaré como si no hubiera terminado el trabajo hasta las siete de la tarde. Así, además de las ventas, también puedo anotar las peticiones que tengo y que no puedo servir. Si no tengo unidades para vender, sólo tengo que pedir disculpas a los clientes. Bueno, para hacer las cosas bien y para redondear los números, veré lo que pasa en 100 días.
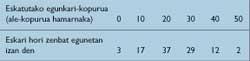
Reconozcamos que nuestro vendedor de periódicos tiene todas las características para hacerse millonario. En consecuencia, Publicis encontró los datos de la tabla 2:
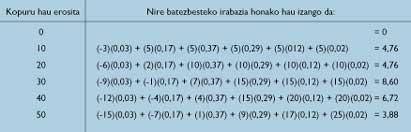
Pensemos —se dice— que el futuro se asemeja al pasado. Sería interesante calcular lo que pasaría si comprara a diario el mismo número de unidades, siendo las cantidades 0, 10, 20, ..., 50. En estas condiciones, utilizando mi tabla de frecuencias, podría calcular el rendimiento total de 100 días. Gracias a esto, dividiendo por 100, me beneficiaría cada día. Por tanto, teniendo en cuenta las tablas 1 y 2, se puede calcular la tabla 3 de rendimientos medios.
El lector puede sorprender al descubrir que un pobre vendedor de periódicos encuentra los principios básicos de probabilidad y estadística. ¿Por qué no puede ser rápido y hábil? El conjunto de los comerciantes de periódicos tendrá que ver con el de gente rápida y competente.
Por lo tanto, si compro 30 periódicos al día mi rendimiento medio diario será de 8,60 libras, ha concluido Publicis mirando la tabla 3.
De este modo se reinventa la media matemática, la mejora de una función económica y el futuro económico.
Pero nuestra historia todavía no ha terminado.
Un amigo de Publicis era un estudiante de matemáticas que le gustaba ser joven, ser bueno y discutir. A los 20 años, en lugar de hablar del tiempo, del futuro o del pasado, prefería hablar de algo más técnico en sus charlas. Así surgió la colaboración entre la Universidad y el comercio.
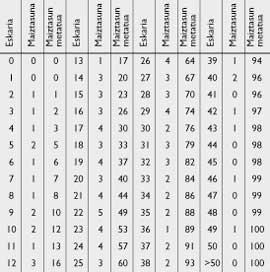
Nuestro joven matemático quería encontrar la fórmula cómoda que podía usar su amigo. En una ocasión se reunieron en un pequeño bar y gracias a los datos exactos tomados por Publicis (ver tabla 4), pudo realizar una declaración más elaborada para facilitar su uso. De la frecuencia de ventas, el amigo de Publicis calculó la curva de frecuencia acumulada que aparece en la figura 1.
El vendedor se preguntaba a sí mismo qué papel iba a desempeñar en su problema.
La noción de probabilidad, tal y como la entendemos, no ha sido objeto de trabajo matemático hasta hace unos 300 años. Sin embargo, dentro de estos seres hay un concepto indeterminado de “suerte”.
Escuchemos una entrevista entre nuestros dos amigos que están en la mesa del bar:
Si el futuro se repite con la misma frecuencia indicada por el pasado —dice el alumno— tienes 12 posibilidades de vender un máximo de 10 periódicos de 100 días, un máximo de 13 periódicos, ..., 44 posibilidades de vender un máximo de 21, (ver tabla 4)
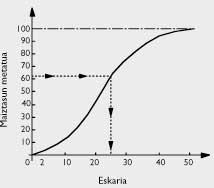
Utilizaremos P(x) como máximo para expresar la probabilidad de vender x periódicos. Muchas veces, gracias a un razonamiento muy sencillo con el nombre de cálculo marginal, descubrirás su rendimiento marginal y, así, cuantos periódicos tendrás que comprar sistemáticamente en los próximos 100 días, siempre con frecuencias pasadas en el futuro.
Pensemos que cada día compras s-1 periódicos. ¿Qué pasaría si decides comprar un ejemplar más? ganaría 0,50 libras con probabilidad 1-P(s-1) y perdería 0,30 libras con probabilidad P(s-1). Por tanto, rendimiento de relleno:
sería 0,50 (1 - P(s-1)) - 0,30 P(s-1) ó 0,5 - 0,8 P(s-1).
Por lo tanto, es interesante comprar un periódico más si entre
0,5 y 0,8 P(s-1) 0 es decir, P(s-1) 0,625
si se cumple. Pero cuando P(s-1) es 0,625 no te interesa.
Por lo tanto, el número de periódicos s que debes comprar (para que puedas obtener el máximo rendimiento) será el que cumpla la condición P(s-1) 0.625 P(s).
Consultando la Tabla 4:
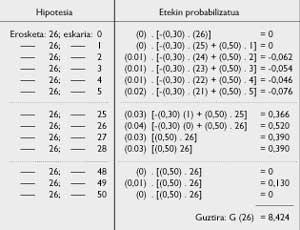
s=26 al ser P(25)=0,60 y P(26)=0,64.
Por lo tanto, el mejor inventario será s = 26.
Pero, ¿cuál será el rendimiento medio correspondiente al inventario s = 26? Se deben analizar las hipótesis de cálculo y todas las probabilidades asociadas. Si G(26) es un rendimiento medio, se obtiene la Tabla 5.
Adicionalmente, se puede calcular el rendimiento medio G(s) si se trata de un inventario s, utilizando la siguiente fórmula de recurrencia:
G (s) = G (s-1) + 0,5 - 0,80 P (s-1)
Como G(0) = 0 se obtiene:
G(1) = 0,50 - (0,80)(0) = 0,50 G(2)
= 0,50 + 0,50 - (0,80)(0) = 1 G(3)
= 1+0,50 - (0,80)
= 1,492 G(4) = 1,492 + 0,50 - (0,80)(0,02)
= 1,976 G(5) = 1,976 + 0,80 (0,80)
y así sucesivamente
G(26) = 8,424; G(27) = 8,376, etc.

Un buen consejo —concluyó el joven estudiante— es comprar cada día 26 periódicos. Así ganarás el máximo medio, es decir, 8,43 libras por día. En cualquier caso, de esta decisión deben suprimirse los días especiales. Por ejemplo: fechas de lanzamiento de satélites (si crees que interesa a tus clientes), fecha de anuncio de bajada de impuestos, etc. Mis consejos para esos días no son válidos.
Como ves, el comercio sigue siendo mentira. Sin embargo, dado que los eventos especiales son así, adapta tu comercio y tu vida a los datos y a los días normales, que son más numerosos. Eso sí, si sientes un deseo de impulsar y desarrollar las ventas, quizá la matemática todavía te pueda dar una pequeña ayuda, pero de eso hablaremos en otro. Kaufman y R. Extraído del libro “Invitación a la Investigación de Operaciones” de Faure.





