El problema dels magatzems

Publicis compra cada exemplar de periòdic en 0,50 lliures i ho embeni en 1 liberal. No obstant això, els exemplars que li queden sense vendre, l'endemà els compra el majorista en 0,20 lliures per unitat. Aquest sistema de venda sembla també col·loquial o cruel, però la societat que s'encarrega de la venda a l'engròs també depèn de la crueltat de l'impressor, que al seu torn depèn dels proveïdors, (i un llarg etcètera). Tot això és una història cruel, la història del nostre marc econòmic.
Per a Publicis els dies feliços són només ocasionals i moltes vegades no té la possibilitat de compensar els seus deutes. La fam és un mal assessor, però qui sap? Pot ser que ens guiï al coneixement i a l'anàlisi estadística.
L'endemà d'un difícil dia de treball, va passar una primera gran etapa per a conèixer la seva trajectòria vital i va decidir fer un balanç de la seva activitat. Segons dades diàries, mai va arribar a vendre 50 unitats el mateix dia. Va aconseguir un màxim de 40 unitats. D'altra banda, amb freqüència venia 30 unitats i amb més freqüència arribava a vendre 20 unitats. Lògicament, aquesta xifra de vendes es va deure a fets polítics o notícies aparegudes en la primera pàgina.
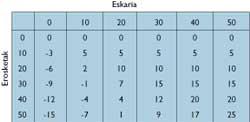
En arribar un a ser home de negocis es converteix en comptador (alguns desitjarien que l'afirmació contrària fos certa). Per això, el nostre heroi ha preparat una taula amb beneficis.
Publicis se sorprèn consultant la taula. Per exemple: Comprant 50 unitats pot guanyar 25 lliures, però arrisca 15 lliures.
L'habilitat en els negocis està gairebé sempre relacionada amb la percepció del futur. Preocupat, el nostre amic està segur que ha d'analitzar el problema de prop. En conseqüència, el diable de l'estadística ha entrat en la seva ment, que, d'altra banda, està bastant mal preparat per a acceptar a un inquilí tan insuportable. A continuació es resumeixen les seves reflexions:
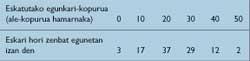
L'important no és el que guanyo un dia, sinó el que puc guanyar en un mes o dos mesos o més. No és possible preveure el que puc guanyar anualment si comprés el mateix nombre de periòdics cada dia? Però, quant hauria de ser aquesta quantitat? I com conèixer el comportament dels clients? Bé, després d'una temporada, una vegada finalitzada la venda del lot diari, en lloc d'abandonar, em quedaré com si no hagués acabat el treball fins a les set de la tarda. Així, a més de les vendes, també puc anotar les peticions que tinc i que no puc servir. Si no tinc unitats per a vendre, només haig de demanar disculpes als clients. Bé, per a fer les coses bé i per a arrodonir els números, veuré el que passa en 100 dies.
Reconeguem que el nostre venedor de periòdics té totes les característiques per a fer-se milionari. En conseqüència, Publicis va trobar les dades de la taula 2:
Pensem —es diu— que el futur s'assembla al passat. Seria interessant calcular el que passaria si comprés diàriament el mateix nombre d'unitats, sent les quantitats 0, 10, 20, ..., 50. En aquestes condicions, utilitzant la meva taula de freqüències, podria calcular el rendiment total de 100 dies. Gràcies a això, dividint per 100, em beneficiaria cada dia. Per tant, tenint en compte les taules 1 i 2, es pot calcular la taula 3 de rendiments mitjans.
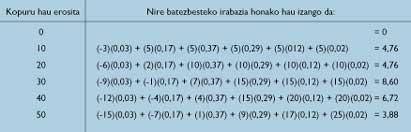
El lector pot sorprendre en descobrir que un pobre venedor de periòdics troba els principis bàsics de probabilitat i estadística. Per què no pot ser ràpid i hàbil? El conjunt dels comerciants de periòdics tindrà a veure amb el de gent ràpida i competent.
Per tant , si compro 30 periòdics al dia el meu rendiment mig diari serà de 8,60 lliures, ha conclòs Publicis mirant la taula 3.
D'aquesta manera es reinventa la mitjana matemàtica, la millora d'una funció econòmica i el futur econòmic.
Però la nostra història encara no ha acabat.
Un amic de Publicis era un estudiant de matemàtiques que li agradava ser jove, ser bo i discutir. Als 20 anys, en lloc de parlar del temps, del futur o del passat, preferia parlar d'una cosa més tècnica en les seves xerrades. Així va sorgir la col·laboració entre la Universitat i el comerç.
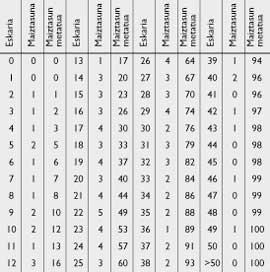
El nostre jove matemàtic volia trobar la fórmula còmoda que podia usar el seu amic. En una ocasió es van reunir en un petit bar i gràcies a les dades exactes preses per Publicis (veure taula 4), va poder realitzar una declaració més elaborada per a facilitar el seu ús. De la freqüència de vendes, l'amic de Publicis va calcular la corba de freqüència acumulada que apareix en la figura 1.
El venedor es preguntava a si mateix quin paper anava a exercir en el seu problema.
La noció de probabilitat, tal com l'entenem, no ha estat objecte de treball matemàtic fins fa uns 300 anys. No obstant això, dins d'aquests éssers hi ha un concepte indeterminat de “sort”.
Escoltem una entrevista entre els nostres dos amics que estan en la taula del bar:
Si el futur es repeteix amb la mateixa freqüència indicada pel passat —diu l'alumne— tens 12 possibilitats de vendre un màxim de 10 periòdics de 100 dies, un màxim de 13 periòdics, ..., 44 possibilitats de vendre un màxim de 21, (veure taula 4)
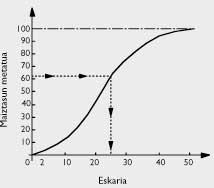
Utilitzarem P(x) com a màxim per a expressar la probabilitat de vendre x periòdics. Moltes vegades, gràcies a un raonament molt senzill amb el nom de càlcul marginal, descobriràs el seu rendiment marginal i, així, quants periòdics hauràs de comprar sistemàticament en els pròxims 100 dies, sempre amb freqüències passades en el futur.
Pensem que cada dia compres s-1 periòdics. Què passaria si decideixes comprar un exemplar més? guanyaria 0,50 lliures amb probabilitat 1-P(s-1) i perdria 0,30 lliures amb probabilitat P(s-1). Per tant, rendiment de farciment:
seria 0,50 (1 - P(s-1)) - 0,30 P(s-1) o 0,5 - 0,8 P(s-1).
Per tant , és interessant comprar un periòdic més si entre
0,5 i 0,8 P(s-1) 0 és a dir, P(s-1) 0,625
si es compleix. Però quan P(s-1) és 0,625 no t'interessa.
Per tant , el nombre de periòdics s que has de comprar (perquè puguis obtenir el màxim rendiment) serà el que compleixi la condició P(s-1) 0.625 P(s).
Consultant la Taula 4:
s=26 en ser P(25)=0,60 i P(26)=0,64.
Per tant, el millor inventari serà s = 26.
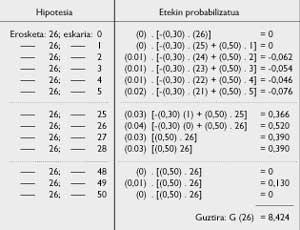
Però, quin serà el rendiment mig corresponent a l'inventari s = 26? S'han d'analitzar les hipòtesis de càlcul i totes les probabilitats associades. Si G(26) és un rendiment mitjà, s'obté la Taula 5.
Addicionalment, es pot calcular el rendiment mitjà G(s) si es tracta d'un inventari s, utilitzant la següent fórmula de recurrència:
G (s) = G (s-1) + 0,5 - 0,80 P (s-1)
Com a G(0) = 0 s'obté:
G(1) = 0,50 - (0,80)(0) = 0,50 G(2)
= 0,50 + 0,50 - (0,80)(0) = 1 G(3)
= 1+0,50 - (0,80)
= 1,492 G(4) = 1,492 + 0,50 - (0,80)(0,02)
= 1,976 G(5) = 1,976 + 0,80 (0,80)
i així successivament
G(26) = 8,424; G(27) = 8,376, etc.

Un bon consell —va concloure el jove estudiant— és comprar cada dia 26 periòdics. Així guanyaràs el màxim mitjà, és a dir, 8,43 lliures per dia. En qualsevol cas, d'aquesta decisió han de suprimir-se els dies especials. Per exemple : dates de llançament de satèl·lits (si creus que interessa als teus clients), data d'anunci de baixada d'impostos, etc. Els meus consells per a aquests dies no són vàlids.
Com veus, el comerç continua sent mentida. No obstant això, atès que els esdeveniments especials són així, adapta el teu comerç i la teva vida a les dades i als dies normals, que són més nombrosos. Això sí, si sents un desig d'impulsar i desenvolupar les vendes, potser la matemàtica encara et pot donar una petita ajuda, però d'això parlarem en un altre. Kaufman i R. Extret del llibre “Invitació a la Recerca d'Operacions” de Faure.





