The problem of warehouses

Publicis buys each newspaper in 0.50 pounds and sells it in 1 liberal. However, the specimens that remain unsold, the next day the wholesaler buys them in 0.20 pounds per unit. This sales system also seems colloquial or cruel, but the society that handles wholesale also depends on the cruelty of the printer, which in turn depends on the suppliers, (and a long etcetera). All this is a cruel story, the history of our economic framework.
For Publicis the happy days are only occasional and many times he does not have the possibility to compensate his debts. Hunger is a bad advisor, but who knows? It may guide us to knowledge and statistical analysis.
The day after a difficult day of work, he spent a first great stage to know his life trajectory and decided to take stock of his activity. According to daily data, it never sold 50 units on the same day. It reached a maximum of 40 units. On the other hand, he frequently sold 30 units and more often sold 20 units. Logically, this sales figure was due to political facts or news appearing on the first page.
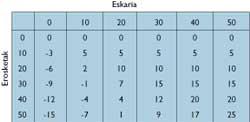
When you become a businessman you become an accountant (some would want the opposite statement to be true). Therefore, our hero has prepared a table with benefits.
Publicis is surprised by the table. For example: Buying 50 units can gain 25 pounds, but risk 15 pounds.
Skill in business is almost always related to the perception of the future. Worried, our friend is sure he has to analyze the problem closely. Consequently, the devil of statistics has entered his mind, which, on the other hand, is quite poorly prepared to accept such an unbearable tenant. Here are his reflections:
The important thing is not what I earn a day, but what I can win in a month or two months or more. Is it not possible to foresee what I can earn annually if I bought the same number of newspapers every day? But how much should that amount be? And how to know the behavior of customers? Well, after a season, once the sale of the daily lot is over, instead of leaving, I will stay as if I had not finished the job until seven in the afternoon. So, in addition to sales, I can also write down the requests I have and cannot serve. If I don't have units to sell, I just have to apologize to customers. Well, to do things right and round the numbers, I'll see what happens in 100 days.
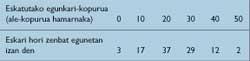
We recognize that our newspaper seller has all the features to become a millionaire. Consequently, Publicis found the data in Table 2:
Let us think, it is said, that the future resembles the past. It would be interesting to calculate what would happen if you bought the same number of units daily, being the quantities 0, 10, 20, .., 50. Under these conditions, using my frequency table, I could calculate the total performance of 100 days. Thanks to this, dividing by 100, I would benefit every day. Therefore, taking into account tables 1 and 2, the average yield table 3 can be calculated.
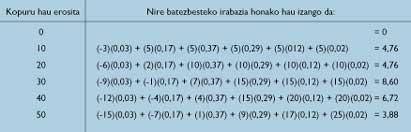
The reader may be surprised to discover that a poor newspaper seller finds the basic principles of probability and statistics. Why can't it be quick and skillful? The set of newspaper traders will have to do with that of quick and competent people.
Therefore, if I buy 30 newspapers a day my average daily performance will be 8.60 pounds, Publicis concluded looking at table 3.
This reinvents the mathematical mean, the improvement of an economic function and the economic future.
But our story is not over yet.
A friend of Publicis was a math student who liked to be young, be good and discuss. At 20, instead of talking about time, the future or the past, he preferred to talk about something more technical in his talks. Thus came the collaboration between the University and commerce.
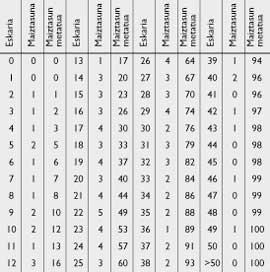
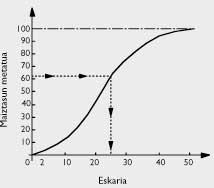
Our young mathematician wanted to find the comfortable formula that his friend could use. Once they met in a small bar and thanks to the exact data taken by Publicis (see table 4), he was able to make a more elaborate statement to facilitate its use. From the sales frequency, Publicis friend calculated the cumulative frequency curve shown in Figure 1.
The salesman asked himself what role he would play in his problem.
The notion of probability, as we understand it, has not been subject to mathematical work until about 300 years ago. However, within these beings there is an indeterminate concept of “luck.”
Let's hear an interview between our two friends who are at the bar table:
If the future is repeated with the same frequency indicated by the past, says the student, you have 12 possibilities to sell a maximum of 10 newspapers of 100 days, a maximum of 13 newspapers, .., 44 possibilities to sell a maximum of 21, (see table 4)
We will use P(x) at most to express the probability of selling x newspapers. Many times, thanks to a very simple reasoning with the name of marginal calculation, you will discover its marginal performance and, thus, how many newspapers you will have to buy systematically in the next 100 days, always with frequencies passed in the future.
Let's think that every day you buy s-1 newspapers. What if you decide to buy one more copy? gain 0.50 pounds with probability 1-P(s-1) and lose 0.30 pounds with probability P(s-1). Therefore, filling performance:
would be 0.50 (1 - P(s-1)) - 0.30 P(s-1) or 0.5 - 0.8 P(s-1).
Therefore, it is interesting to buy one more newspaper if
between 0.5 and 0.8 P(s-1) 0 i.e. P(s-1) 0,625
if it is fulfilled. But when P(s-1) is 0.625 you are not interested.
Therefore, the number of newspapers you need to buy (so you can get the maximum performance) will be the one that meets the condition P(s-1) 0.625 P(s).
Looking at Table 4:
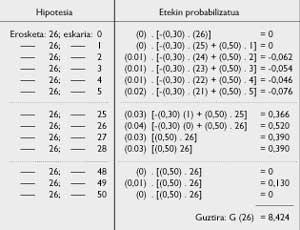
s=26 being P(25)=0.60 and P(26)=0.64.
Therefore, the best inventory will be s = 26.
But what will be the average performance corresponding to inventory s = 26? The calculation hypotheses and all associated probabilities should be analyzed. If G(26) is an average yield, Table 5 is obtained.
Additionally, the average yield G(s) can be calculated if it is an inventory s, using the following recurrence formula:
G(s) = G (s-1) + 0.5 - 0.80 P (s-1)
As G(0) = 0 you get:
G(1) = 0.50 - (0.80)(0) = 0.50 G(2)
= 0.50 + 0.50 - (0.80)(0) = 1 G(3)
= 1+0.50 - (0.80)
= 1.492 G(4) = 1.492 + 0.50 - (0.80)(0.02)
= 1.976 G(5) = 1.976 + 0.80 (0.80)
and so on
G(26) = 8,424; G(27) = 8,376, etc.

A good advice, the young student concluded, is to buy 26 newspapers every day. Thus you will earn the average maximum, that is, 8.43 pounds per day. In any case, special days should be deleted from this decision. For example: satellite launch dates (if you think your customers are interested), tax drop announcement date, etc. My advice for those days is not valid.
As you see, trade remains a lie. However, since special events are like this, adapt your trade and your life to the most numerous data and normal days. Yes, if you feel a desire to boost and develop sales, perhaps math can still give you a little help, but that's what we'll talk about in another. Kaufman and R. Extracted from the book “Invitation to Operations Research” by Faure.





