Historia del Abaco

Como comentamos al inicio de la historia de las cifras, antes de que aparecieran el alfabeto y las cifras, los seres humanos utilizaban principalmente dos sistemas de contabilización, el de las muescas y los cantos. Lo que nos interesa ahora es el de los cantos, ya que es el origen de los ábacos.
En algunos pueblos, para contabilizar a los soldados o a las ovejas, los cantos se depositaban en zanjas excavadas en el suelo; se apilaban diez cantos y se sustituían por otra piedra mayor, es decir, se utilizaba la base diez. Cada zanja representaba una remodelación de diez. En otros pueblos, las zanjas eran sustituidas por placas de hierro o estrabos de madera y los bolos perforados para poder moverse por las planchas o estribos. Así nacieron los marcadores de bolas.
Con la palabra Abako indicamos tres calculadoras diferentes. El primero, utilizado por muchas culturas antiguas, era el tablero roto o la propia tierra. Las cifras o símbolos geométricos podían escribirse con un dedo o con una cuña. En general, la palabra griega abax significa tabla llana o mesa sin patas. Su origen podría ser la palabra hebraica abaq, cuyo significado es polvo. Los hindúes utilizaron este tipo de ábacos VI. Hasta el siglo XX para realizar cálculos con sus cifras.

El segundo tipo de calculadora es el de tablas. En estas tablas se dibujaban líneas paralelas que indicaban un orden numérico. Para realizar los números y cálculos se colocaban encima unas corridas o fichas. A estas piezas los griegos llamaban los psehones y los romanos calculi. Estas líneas podían ser trazadas sobre pergamas, talladas en mármol, talladas en madera o bordadas en telas.
En los ábacos de Roma, cada columna (o fila) representaba una recomposición de diez; de derecha a izquierda y empezando por las unidades. A veces la columna estaba dividida en dos partes. En la parte inferior una ficha indicaba una unidad del orden correspondiente. En la parte superior, sin embargo, una ficha valía la mitad de una unidad del orden siguiente (o cinco unidades del orden correspondiente). Esto es en la primera columna 5, en la segunda 50, etc.
En un bajorrelieve de un sarcófago romano del siglo I, un joven calculator, con cuentas en las casas de los mayoristas, puede verse ante su maestro con una calculadora móvil de estas características.
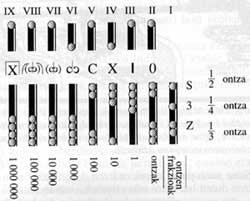
El móvil de Abako era una tableta metálica con ranuras paralelas. A través de las rendijas se movían los botones de tamaño adecuado. Cada rendija correspondía a un orden decimal, a excepción de los dos primeros de la derecha. Estos se utilizaban para la docena o crianza del AS y para la mitad, tercio y cuarto de la vajilla. Así, la tercera ranura derecha a las unidades, la cuarta a las diez, etc. correspondientes. Además, cada una de las ranuras (excepto la primera) estaba dividida en dos partes, con cuatro botones en las inferiores y un botón en las superiores. Los botones de abajo valían una unidad de orden y los de arriba cinco. Esta calculadora móvil se asemeja mucho a los marcadores de bolas utilizados en Países de Extremo Oriente y Próximo Oriente.
Desde la destrucción del Imperio romano hasta el final de la Edad Media, en la Europa occidental estuvo en manos de unas pocas ciencias. Estos, una vez aprendidos a leer y a escribir, abordaban temas como la Astronomía, la Geometría o el Cálculo. El cálculo lo hacían con los dedos y escribían la cifra en romano. Hay que decir que sólo los especialistas sabían realizar operaciones aritméticas y las realizaban mediante ábacos romanos. En la actualidad, el especialista de la época necesitaba muchas horas para realizar la operación que un niño podía realizar en pocos minutos. Cuando las cosas estaban así, los que querían tomar conciencia del cálculo se dirigían hacia Italia, que entonces tenía un mayor contacto con árabes y byzanzios, y sus clases eran especializadas en operaciones complejas.
En el año 999 fue nombrado Papa Gerbert d’Aurillac. Anteriormente había estudiado los métodos árabes e intentó penetrar por Europa, pero encontró una gran resistencia. En un principio, los símbolos árabes (hindúes) introducidos por Gerbert fueron escritos en fichas de hueso de rama y sustituyeron a los cantos en las columnas del ábaco. Sin embargo, los calculadores retrógrados prefirieron imprimir cifras romanas.
Entre los años 1095 y 1270 destaca la de Cruzada. Si su objetivo era destruir las ideas de los infieles, obtuvieron otros resultados. Una de ellas fue la toma de conciencia de la cultura que algunos caballeros y clérigos presentes querían eliminar. En cuanto al cálculo, conocieron el cero y las técnicas hindúes de cálculo.
Además, al otro lado del Mediterráneo, en la Península Ibérica, concretamente en Toledo, se intensificaron los contactos entre ambos mundos. Desde finales del siglo XX. Estos dos hechos dieron lugar a la muerte del ábaco.

La muerte se aceleró en el siglo XIII. A principios del siglo XX, el matemático Leonardo Fibonacci de Pisa, autor del libro "Ábaco Abaci". Este tratado no afectó, como se podía imaginar, a la aritmética del ábaco, sino a las reglas del cálculo de cifra sobre la arena. Por ello se convirtió en manual de apoyo al algoritmo. En consecuencia, la ciencia de los cálculos mediante cifras (la aritmética) se extendió al pueblo llano. La sencillez de este cálculo hizo que la propia Iglesia cuestionara si la nueva aritmética no tenía algo mágico o demónico. De ahí a quemar en el fuego a unos fogosos partidarios de Fibonacci sólo había un paso, dado por algunos inquisidores.
La verdad es que la disputa entre los abaquistas y los algorítmicos se extendió durante siglos y tras ganar nuevos métodos se utilizaba el ábaco. XVIII. En el siglo XVIII los cálculos en pluma se verificaban mediante ábaco. Mientras los nuevos cálculos fueron conquistados por el científico, comerciantes, banqueros, funcionarios, etc. siguieron utilizando el ábaco.

La revolución francesa acabó decidiendo la cuestión. En aquella época se prohibió el uso escolar del ábaco.
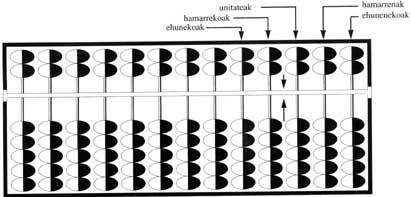
El tercer tipo de ábaco es el de los marcadores de bola. Los marcadores se utilizan principalmente en Países del Este: En la Unión Soviética, China, Japón, Singapur, Corea, Taiwán, etc. En ellas veremos tres tipos diferentes: Tipos de stchoty en el fuego chino, pan, sorobe japonés y stchoty ruso.
En el fuego de China el origen de la pana es desconocido, pero sabemos que el XVI. En el siglo XX ya se utilizaba. En el fuego (calcular) en el ideograma chino se ve un ábaco, un ideograma en el que la mano representa debajo y encima el bambú. En el fuego la pana está formada por cuatro listones o estribos que forman un rectángulo, varios palos de bambú (8-15) unidos a los estribos largos, otro estrabe que separa estos palos en dos partes (parte superior e inferior) y dos en la parte superior y cinco en la inferior, y siete bolas móviles de arriba a abajo. Por supuesto, cuantos más bastones tengamos, mayor será el número que se podrá indicar.
En general, los dos palos de la derecha (columnas) se dejan para los de la décima y la centésima, quedando las unidades en la tercera. Las bolas de la parte inferior valen una unidad del orden correspondiente, mientras que las de la parte superior valen cinco. Las bolas superiores e inferiores para representar los números se llevan al estrabe intermedio.
Sin sus labios, el llamado Soroban de Japón fue trasladado desde China, en el siglo XVI. En el siglo XX, apika. XIX. Conservó su aspecto original hasta mediados del siglo XX. Después se fue perdiendo una bola superior y II. Desde la Guerra Mundial perdieron la quinta bola de la parte inferior que sobraba. En Japón todavía se celebran competiciones de cálculo por ábaco o campo. En su día fue muy popular una competición de cálculo celebrada en 1945. En ella Kiyoshi Matsuzaki, campeón japonés de campo, se impuso en cuatro de cada cinco pruebas a Thomas Nathan Woods, el operador más experto en calculadoras electrónicas del ejército estadounidense en Japón.
Los soviéticos conocieron la stchotya a través de los árabes. Prueba de ello es su utilización en algunas regiones de la India y Oriente Próximo. Los turcos llaman choreb a las coulbas y armenias.

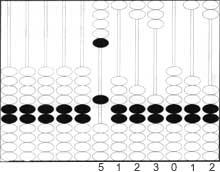
El stchoty de la Unión Soviética no es igual a los anteriores. No hay estribos intermedios. Cada palo tiene diez bolas, las dos centrales (5 y 6) de diferentes colores. En algunos stchotys, en algunos bastones sólo se colocan cuatro bolas para las fracciones de rublo y copecas. En el stchoty, las bolas de números deben ir al estrabe superior.
Estos tres marcadores de bolas son actualmente utilizados por mucha gente en sus pueblos, pero sobre todo por comerciantes y comerciantes.
Por último, señalar que en los últimos años se ha reconocido la utilidad de la enseñanza de la aritmética a los niños ciegos y que en las escuelas también se están obteniendo buenos resultados en didáctica de las matemáticas.
Hasta ahora hemos hablado de la historia del abaco, pero para que no sea historia y para recuperarla de la historia, en el próximo número te daremos la normativa de uso del abaco chino. Para ello le recomendamos que, si es posible, disponga de un ábaco chino. Por supuesto, en un primer momento te atascos los dedos, te mueves las bolas, te equivocarás en los cálculos, pero te resolverás con experiencia y paciencia.