Spaghetti of the universe

Urrestilla, Jon

Fisikan doktorea eta Sussexeko Unibertsitateko ikertzailea

Speaking of one-dimensional objects (strings) in basic physics, we come to mind several options. On the one hand we have superstrings. In recent years, physicists and mathematicians have worked enormously on the theory of superstrings. The fundamental idea is that elementary particles are not punctual but one-dimensional dispersed objects. Somehow, the particles are not some "balls", but some "sokitas" that vibrate. But on the other hand, scientists have also investigated another type of string: cosmic strings. And although both are "strings", they have nothing to do with each other. In this article we will talk about these last strings.
Spaghetti of the universe
01/10/2009 | Jon Urrestilla | Doctor of Physics and Researcher at the University of Sussex
If one of the universe phase transitions were equivalent to the conversion of liquid water into ice, the study of ice trapped streams would allow the ancient universe to be known.
Dmitry Maslov/350RF

Cosmic strings are topological errors. When the universe was very young, there were transitions of cosmological phase that could lead to errors and that are cosmic strings.

Let's try to understand it with an analogy: suppose one of the transition phases of the universe is something equivalent to the conversion of liquid water into ice. Therefore, at high temperatures we would have liquid water and when the temperature drops the water would become ice. But it is possible (according to the theory we use) that streams of liquid water appear inside the ice. If this happened, those who live in a cold phase (ice), we can observe how the warm phase was observing these streams. These streams are analogous to the defects, the fragments of high temperature (streams) that have remained in the phase of low temperature (ice).

Very high energies

The errors that predict high-energy cosmological models have, in most cases, rope form, that is, they are one-dimensional objects. In addition, they have incredible properties: although they have a much smaller width than that of an atom (perhaps the width of a proton), the length is measured in light years (they extend throughout the entire universe). The mass is also huge: a one kilometer rope would have the same mass as Earth! It may be helpful to have a normal mental image: the cosmic strings are similar to those of very long spaghetti, very fine and of great mass.

In cosmology it is very difficult to detect errors and, in some way, they are only known in the theoretical field. But in other areas of physics, errors occur. In the physics of condensed matter, for example, defects appear in liquid crystals, ferromagnetic materials, superconductors, etc. These errors can be analyzed in laboratory, which allows an interesting relationship between condensed matter and cosmology. In any case, although they have not been seen in cosmology, it is quite logical to think that errors can be in the universe, since they exist in other areas of physics.

Cosmic strings are possible in many high energy theories, including the theory of superstrings (thus, although with totally different concepts, superstrings and cosmic strings have some links). And, if they appeared, they would appear in a very high energy, much higher than what can be obtained in particle accelerators. Finding strings would be a great advance for basic physics. For many, cosmic strings are one of the few possibilities to directly test the theory of superstrings.

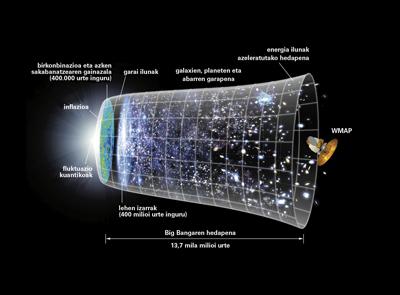
Representation of the creation and evolution of the universe.
(Photo: WMAP (NASA)

But, as we have said, it is very difficult to observe directly the cosmic strings. Imagine that the cosmic strings were formed in the newborn universe. At that time the universe seemed to spin a plate. But as the universe cools down and grows, the string density was decreasing. Now only a few spaghetti are on our plate (our observable universe). Being close to us is a very unlikely fact. Therefore, instead of directly measuring the strings, we should measure their indirect effects, for example by means of the effect of the strings on the microwave background radiation (CMB) or by the effect of the gravitational lens.

Indirect evidence

The gravitational lens is a phenomenon known in astrophysics: if there is an object of great mass between a galaxy far from us and us (for example, a group of galaxies), the light of the distant galaxy deteriorates as a consequence of that intermediate object and the image is distorted. The analysis of the distortion allows to deduce the properties of the central object with mass. Likewise, if there were a cosmic cord between the remote galaxy and us, the image would be distorted, but the distortion produced by the strings and the distortion caused by any other mass are different. In the case of the normal effect of the gravitational lens (produced by high-mass astrophysical objects, such as clusters of galaxies), numerous images of a single remote object will appear, usually in the form of a ring or arc. In the case of the gravitational lens effect that the strings will produce, multiple images of the remote object will also occur, but, unlike in the other case, all images will have the same aspect, as if they were repeated.

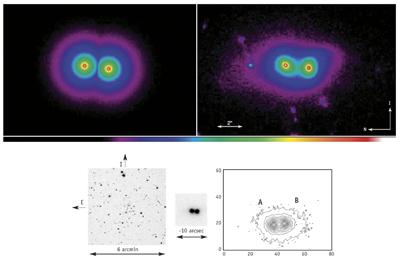
This is what they saw when they observed the object called CSL-1 (Capodimonte-Stenberg-Lens, 1st candidate): two galaxies very similar to each other. To explain an object of this type, there are only two possibilities: the effect of the gravitational lens produced by a cosmic cord (therefore, two identical images of a single galaxy), or that two galaxies with very similar properties (both in photometry and in spectroscopy) are together (from our point of view). Both options are very unlikely and to know the actual response, more accurate observations were made. When the Hubble Telescope observed the CSL-1, it observed that both images were not exactly the same. It was not a string, but two similar galaxies. The team that found the CSL-1 is still looking for more objects of this type, hoping to find a rope.

The object CSL-1 was a candidate for the cosmic string. When they observed with the Hubble telescope (top right) they saw that they were two adjoining galaxies, not the effect of a cosmic string.
(Photo: M. M. Sazhin et al.)

The other possibility we have mentioned is CMB, microwave background radiation. The CMB is very homogeneous, but it has some anisotropies, some granules. These grains, although small, have been measured in cosmological experiments. We know the paradigm that explains very well the anisotropy: inflation. According to inflation, the universe grew exponentially in the short term. But it can also be the formation of cosmic strings at the end of inflation. By moving the strings through the universe they will provoke perturbations and attract matter. These perturbations will also form anisotropy, in addition to anisotropy generated by inflation. If there were cosmic strings, we could measure these "extra" perturbations generated in the CMB and detect the strings indirectly.

The cmb anisotropies that would generate cosmic strings can be simulated by supercomputers and compared with the temperature anisotropies of CMB measured by cosmological experiments. Take the best available cosmological data, such as those provided by WMAP. Using inflation models, we try to adjust the data as best as possible. Now, taking into account also the extra perturbations generated by the strings, we will also adjust the data. Through this analysis, numerical experiments tell us that if we take into account cosmic strings, we can better explain the data. We cannot say with certainty that we have found strings. In addition, with other cosmological data (in addition to the CMB) the existence of strings is not so evident. We need new and more accurate data. Perhaps the Planck satellite that took off in May will help us. Planck will measure the CMB with great precision, both temperature anisotropy and polarization anisotropy. Other experiments will also perform new measurements.

Planck satellite. The data you will collect can help confirm the theory of cosmic strings.
ESA ESA

But in any case, with the current data, we can affirm that the data do not say that there are no strings. And the simple detection of strings is very important. If the new data makes it clear that the strings were not formed, we will have to discard some cosmological models and, perhaps, create new models. On the other hand, if we can observe the strings, we will see the relics of the newborn universe, a unique opportunity to see how the newborn universe was.

BIBLIOGRAPHY BIBLIOGRAPHY
Vilenkin, A.; Shellard, E. P. P. S: Cosmic Strings and Other Topological Defects, Cambridge University Press.
Sazhin, M. et al. : Mon. Not. Roy. Astron. Soc 376 (2007), 1731; Mon. Not. Roy. Astron. Soc 343 (2003), 353. (Figure CSL 1).
Bevis, N.; Hindmarsh, M.; Kunz, M.; Urrestilla, J.: "Fitting CMB data with cosmic strings and inflation", in Phys Rev Let 100, 021301 (2008). (Image of the cosmic strings of the table).
http://map.gsfc.nasa.gov/(WMAP image).
http://www.rssd.esa.int/index.php?project=Planck (Fig. Planck).
Cosmic strings and superstrings
In principle, these two objects have no relation, but the name. Both are "strings", since both are one-dimensional, but they are totally different objects.
Superstrings are part of a theory. To describe high energy physics we have a standard model, and the theory is really successful. However, we do not know how to unify the standard model with the theory of gravity, or, using other words: we do not have quantum theory of gravity. Well, the theory of superstrings is the one that has the best future to get that "theory of everything".
In the standard model the particles are punctual, for example, if we imagine the electron is a kind of "ball". In the theory of superstrings, on the contrary, the basic components are one-dimensional objects, not specific objects. These are the superstrings and, as components of quantum gravity, are very small (~10 -33 cm). Normal known particles (electron, etc.) would be the vibrations of these superstrings.
There are several theories of superstrings; the theory of superstrings is not the only one. But all theories need extra dimensions to be mathematically solid; our 3+1 daily dimensions (3 spatial dimensions + time) are not enough. According to the model, they need 10 or 26 dimensions.
To the left, representation of superstrings. On the right, cosmic strings. In the name they have the greatest relationship, since they are totally different objects.
(Photo: Jean Fran ois Colonna/N. Bevis))
Cosmic strings, on the other hand, are not basic elements of theory, but the consequences of phase transitions that occur in the theories of the fields. Various physical theories predict phase transitions and cosmic strings are topological errors that form in cosmological phase transitions. Errors can have several dimensions: dimensions 0 are called monopoles; unidimensional, rope; two-dimensional, domain wall.
As we have said, cosmic strings are not basic structures, but are formed by something basic. In general, as they appear in the theories of the fields, they will be configured by areas. For example, we can imagine a "conventional" cosmic cord as a tube carrying magnetic field. In general, cosmic strings are very long and our 3+1 dimensions are sufficient for them, as they appear in "normal" zonal theories.
Using the aquatic analogy of the text, the cosmic ropes would be the rivers of water that remained in the ice; the lines of liquid water. The superstrings would be the components that form the water, and the water atoms, both in ice and liquid water, would be the vibrations of the basic superstrings. That is to say, the basic structures that form our aquatic universe (water atoms) are superstrings; the errors that this universe generates when passing from the liquid to the ice (the rivers of liquid water trapped in the ice) are cosmic strings.
However, the situation is somewhat more complicated. If the theory of superstrings is the "theory of everything", we can use it to explain cosmology. If, with superstrings, we explain cosmology, we will see that phase transitions occur. And in these transitions, one-dimensional long objects may appear. Therefore, cosmic strings not only arise in the theories of the fields, but they can also appear in the theories of the superstrings: We have cosmic superstrings!
Physicists would like to see if the theory of superstrings is the true theory that appears in nature, but it is not easy (although we know that cosmic strings can be observed through the CMB). Let us imagine, however, that through cosmological experiments we find cosmic strings. Let us also imagine that we know exactly that the perturbations caused by "normal" cosmic strings and cosmic superstrings are different and we know how to differentiate them. Then, for the first time, we would be directly studying the theory of superstrings. That is to imagine a lot and we still have to do a lot of work, both theoretically and experimentally. But it can really be a perfect opportunity to see more closely the "theory of everything".
Jon Urrestilla
Services Services Services
257 257
2009 2009 2009 2009 2009
Services Services Services
021 021 021 021 021 021
Astrophysics Astrophysics
Free of charge Free
Management Management Management
Babesleak
Eusko Jaurlaritzako Industria, Merkataritza eta Turismo Saila