NAVIER-STOKES: atrapado no remolino de preguntas

Fricción, orixe dos quebradizos de cabeza

Fluxo sanguíneo a través das arterias do corazón, movemento das correntes e nubes de aire atmosférico, ou fluxo ao redor das aspas dun avión: podemos formar una lista interminable de fenómenos físicos relacionados coa dinámica dos fluídos. Da man dos grandes nomes da física e as matemáticas, ao longo da historia foron numerosos os esforzos por comprender e prever estes fenómenos. Como podiamos esperar, debemos ir ao dominio das luces paira atopar os primeiros bosquexos das ecuacións diferenciais que describen a dinámica dos fluídos “ideais”. En concreto, en 1755 Leonhard Euler presentou a ecuación diferencial dos “fluídos ideais”, supondo que a fricción entre as partículas de fluído fronte ás forzas de inercia era despreciable, como en saltos de auga e, en xeral, nos fluxos de alta velocidade.

Aínda que foi un gran avance, por exemplo, paira calcular o movemento lento do mel, a ecuación de Euler falla, xa que a viscosidad do fluxo (as forzas de fricción) ten máis importancia fronte ás forzas inerciales. O mesmo problema prodúcese na resolución dos fluxos en relación cos sólidos ou obstáculos, xa que cerca do obstáculo xéranse grandes gradientes de velocidade debido ás forzas de fricción. Fronte a isto, en 1822 Claude-Louis Henri Navier e vinte anos despois George Gabriel Stokes engadiron á ecuación de Euler a influencia do rozamiento do fluído viscoso ou viscoso, formulando o que hoxe coñecemos como ecuacións de Navier-Stokes. A continuación atópanse dous principios básicos aplicados a unha partícula de fluídos: a conservación da masa (ecuación de continuidade) e a segunda lei de Newton, que relaciona a taxa de crecemento do momento da partícula do fluído (á esquerda da ecuación) coas forzas de presión, gravidade e fricción que o provocan (á dereita da ecuación).

Nos recunchos máis escuros das matemáticas

Como é habitual, paira chegar á solución de ecuacións diferenciais é necesario establecer condicións iniciais. Neste caso, debemos proporcionar ás ecuacións de Navier-Stokes (una ecuación en cada dirección) una distribución de velocidade e presión do fluxo nas tres dimensións do espazo nun momento dado. A partir de aí, as ecuacións deberían devolver a velocidade e a presión do fluxo en calquera momento do futuro. Que suporía isto? Por exemplo, seriamos capaces de predicir exactamente os fenómenos meteorolóxicos ao longo do tempo, de definir completamente o movemento das correntes oceánicas e das ondas, de resolver con precisión a aerodinámica ao redor dos corpos… Se isto fose posible, probablemente, veriamos e entenderiamos a realidade doutra maneira. Lamentablemente, transcorridos dous séculos, a solución analítica só se coñece paira aqueles fluxos que cumpren certas condicións. Basta con fixarse na ecuación da causa: as derivadas parciais de segunda orde (nas forzas de rozamiento) e as non linealidades (na aceleración convectiva) presentan enormes dificultades á hora de resolver analiticamente as ecuacións.

Aínda que pareza mentira, desde o punto de vista de físicos e enxeñeiros, as ecuacións poden describir a realidade con total fiabilidade, como é posible? Paira iso utilízase una ferramenta matemática habitual: resolver ecuacións mediante métodos numéricos, escribindo cada termo da ecuación de forma algebraica e aplicando determinadas condicións de contorno, obtendo solucións aproximadas.

Á esquerda: A distribución de temperatura nunha chama de hidróxeno mediante o cálculo CFD, o espazo está formado por elementos discretos. Dereita: Imaxe da chama obtida nas medicións de laboratorio. Ed. Gontzal Lopez Ruiz

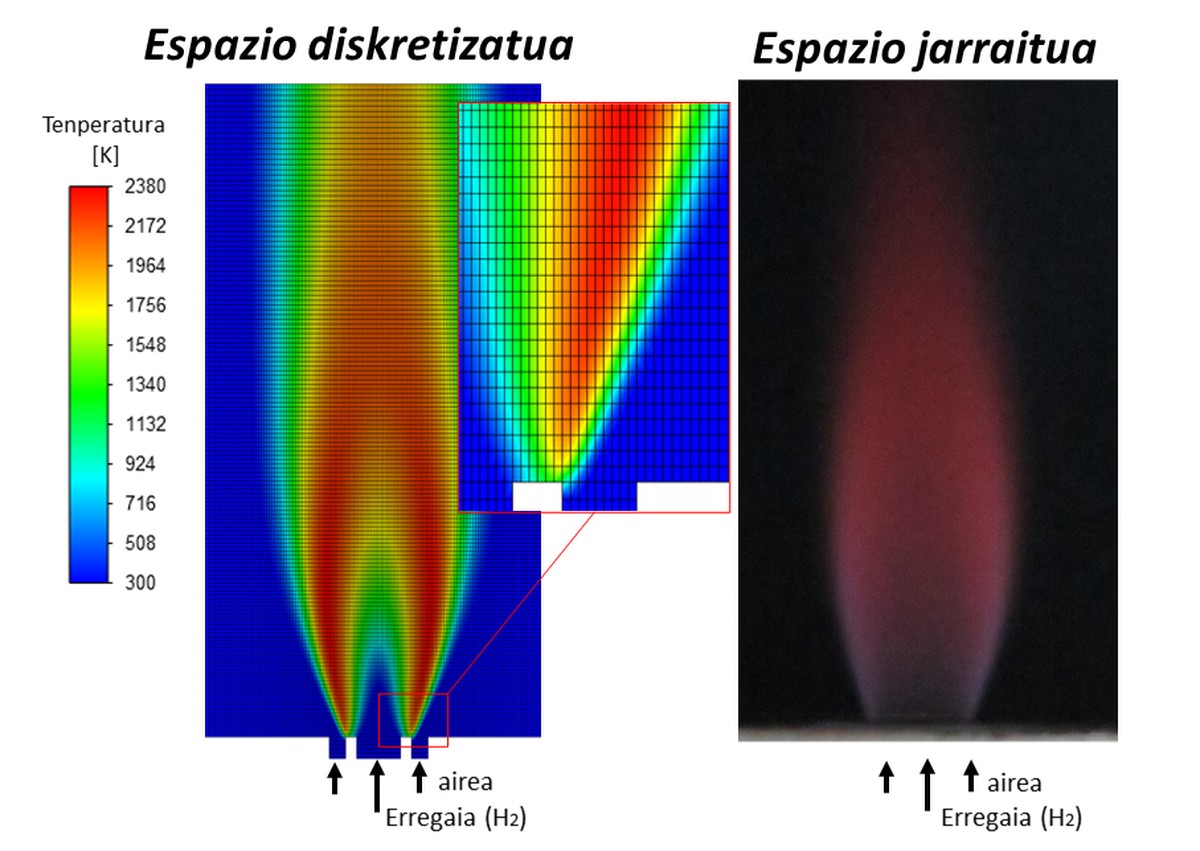
A disciplina coñecida como “Computational Fluíde Dynamics” ou CFD, resolve as ecuacións de Navier-Stokes a través da álxebra de matrices nos fluxos laminos e turbulentos. A pesar de que o custo do cálculo computacional pode ser moi elevado en función do problema exposto, nas últimas décadas esta ferramenta de simulación cobrou forza en diversos ámbitos da investigación e a industria. De feito, o movemento dos fluídos pode ir acompañado da simulación da transferencia de calor, as reaccións químicas ou as deformacións dos sólidos producidos polos fluídos, resolvendo problemas multi-físicos que se dan na realidade. Na arte, os matemáticos traballan paira demostrar a existencia e a soidade das solucións.

Fóra da realidade?

En 1933, o matemático Jean Leray demostrou a existencia e soidade das solucións “débiles” das ecuacións considerando un pequeno intervalo de tempo [3]. Si, como se pode ver, simplificou moito o problema. Fronte a solucións suaves, mediante unha formulación débil pódense atopar solucións non diferenciais que poden presentar a ecuación, facilitando como punto de partida a aprendizaxe da existencia e a soidade das ecuacións. Este importante antecedente levou aos matemáticos a adoptar una nova posición ante o problema, segundo Tristan Buckmaster, da Universidade Princeton, “una das estratexias sería demostrar que as solucións débiles de Leray son suaves, e si conseguísese resolvería o problema do milenio” [2]. Solucións suaves describirían completamente a realidade física, dispondo dunha solución en cada un dos puntos da área considerados en calquera momento (solucións de zonas de velocidade e presión). A clave e a principal dúbida dos matemáticos é que ao pór en marcha o cálculo considerando una formulación suave, pódense obter vectores de velocidade adecuados ao longo do tempo, pero é posible que de súpeto os resultados devolvan a velocidade infinita nalgún punto do campo: as ecuacións estouraron.

Neste sentido, os últimos avances intensificaron as súas dúbidas. No artigo publicado en 2017 polos matemáticos Tristan Buckmaster e Vlad Vicol da Universidade de Princeton [4], paira certas definicións de solucións “débiles”, cuestionouse a soidade das solucións de Leray. Estes resultados permiten, a partir dunhas condicións iniciais, chegar a situacións fisicamente imposibles. No entanto, exponse dúbidas sobre os resultados expostos no artigo; é posible que as solucións consideradas “débiles” incidan no resultado final e exista una soidade paira as solucións “menos débiles”.

Necesidade de simulacros

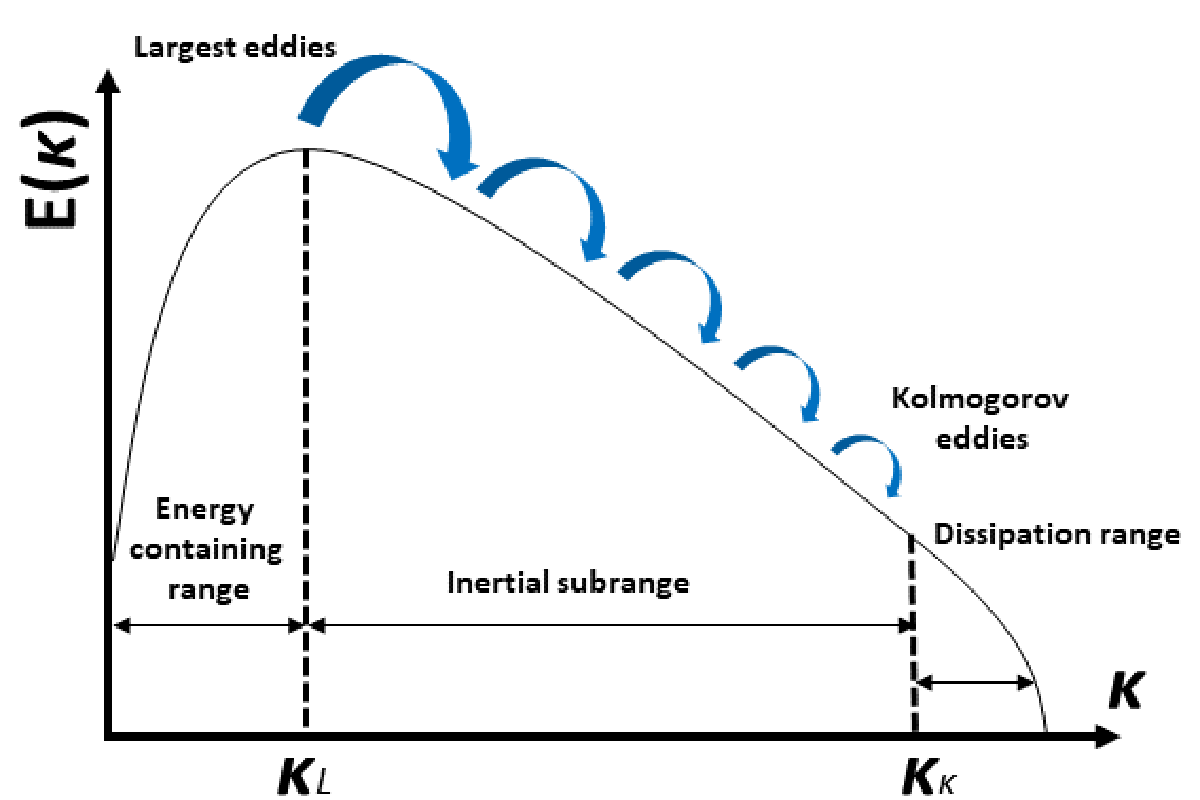
Como se comentou, os métodos numéricos e algoritmos desenvolvidos nas últimas décadas permiten resolver de forma aproximada as ecuacións de Navier-stokes. Con todo, dentro dos cálculos CFD existen una serie de problemas cuxo principal reto é o desenvolvemento de modelos físicos adecuados paira simular o fluxo turbulento xunto con outros fenómenos (reaccións de combustión, deformacións de obxectos, transferencia de calor). A característica principal dos fluxos turbulentos é o movemento caótico e desordenado das partículas, formado por turbulencias a diferentes escalas. Por tanto, as traxectorias das partículas de fluído sofren ao longo do tempo fortes cambios de dirección e velocidade, dificultando o cálculo por métodos numéricos. Paira comprender a relación de remolinos a diferentes tamaños ou escalas definiuse o espectro ou escala de enerxía cinética turbulenta [5]. Segundo esta escala, os remolinos grandes transmiten enerxía cinética a través do espectro aos turbulentos menores de tamaño similar, chegando a escalas pequenas e ata que a viscosidad do fluído disipa os remolinos. Pódese dicir que o espectro nos mostra a competencia entre as forzas de inercia e fricción.

Espectro de enerxía cinética turbulenta. Ed. Gontzal Lopez Ruiz

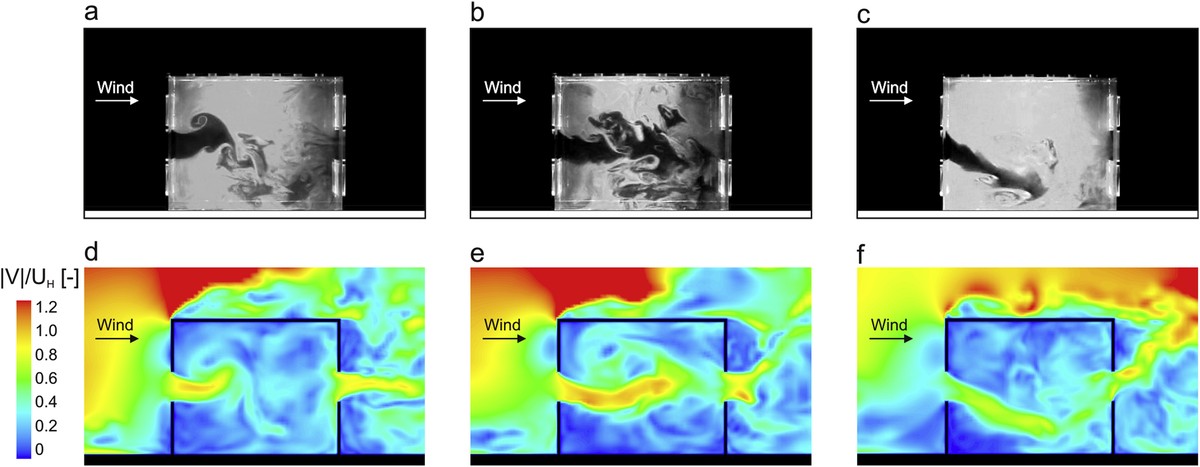
En base a este concepto desenvolvéronse diferentes modelos en función do tamaño de bulebule que se pretende resolver. Por exemplo, resolver toda a escala mediante métodos numéricos nos puntos do espazo considerado (coñecido como Direct Navier-Stokes ou DNS) é un luxo ao alcance duns poucos, xa que paira resolver os tempos e espazos tan pequenos nas turbulencias máis pequenas é necesario utilizar cálculos por super-computador. Co fin de reducir o custo computacional, os modelos turbulentos máis habituais establecen filtros a escala, resolvendo una parte (turbulentos elevados) e modelando outra (turbulencias menores). Nos últimos anos esta técnica, coñecida como Large Eddy Simulation ou LLES, tomou forza na investigación de problemas físicos e no desenvolvemento de deseños dirixidos a diferentes sectores.

Prototipo de estudo de ventilación de vivendas: Experimentos en túnel de vento e simulacións LLES. Ed. T. van Hoof e colaboradores [6] - CC BY NC ND

Aínda que esperamos resolver a realidade a través destas ecuacións, non debemos esquecer que as ecuacións diferenciais son aproximacións xeradas polo home. O premio do Instituto de Matemáticas Clay terá que esperar a que o traballo continuo dos matemáticos dea resultados claros. Ademais, co obxectivo de reducir o custo computacional e mellorar a precisión de solucións aproximadas mediante métodos numéricos, os investigadores traballan neste campo da ciencia en desenvolvemento. A frase que pon en boca do físico Werner Heisenberg resume ben a magnitude do reto: “Cando me atopo con Deus voulle a facer dúas preguntas: Por que a relatividad? E por que a turbulencia? Estou seguro de que terá resposta á primeira pregunta”.

BIBLIOGRAFÍA:

[1] Fefferman C. 2006. “Existence and smoothness of the Navier-Stokes equation”, Millennium Prize Problems, Clay Math. Inst., Cambridge, MA, 2006, 57-67, URL: https://www.claymath.org/sites/default/files/navierstokes.pdf

2] K. Hartnett 2017 Mathematicians Find Wrinkle in Famed Fluíde Equations. Quantamagazine. URL: https://www.quantamagazine.org/mathematicians-find-wrinkle-in-famed-fluíde-equations-20171221/

[3] Leray J. 1934. “Sur lle mouvement d’un liquide visqueux emplissant l’espace”. Acta Math., 63(1), 193–248.

[4] Buckmaster T. e Vicol V. 2019. “Nonuniqual of weak solutions to the Navier-Stokes equation”. Ann. of Math. (2) 189 (2019), non. 1, 101–144.

[5] Kolmogorov A.N. 1941. “Dissipation of energy in locally isotropic turbulence”. Doc. Acad. Nau. SSSR, 32, 16-18.

[6] van Hooff T., B. de Block e Tominaga E. 2017 “On the accuracy of CFD simulations of cros-ventilation flows for a generic isolated building: Comparison of RANS, LLES and experiments”. Building and Environment, 114, 148-165.