NAVIER-STOKES: atrapado en el remolino de preguntas

Fricción, origen de los quebraderos de cabeza

Flujo sanguíneo a través de las arterias del corazón, movimiento de las corrientes y nubes de aire atmosférico, o flujo alrededor de las aspas de un avión: podemos formar una lista interminable de fenómenos físicos relacionados con la dinámica de los fluidos. De la mano de los grandes nombres de la física y las matemáticas, a lo largo de la historia han sido numerosos los esfuerzos por comprender y prever estos fenómenos. Como podíamos esperar, debemos ir al dominio de las luces para encontrar los primeros bocetos de las ecuaciones diferenciales que describen la dinámica de los fluidos “ideales”. En concreto, en 1755 Leonhard Euler presentó la ecuación diferencial de los “fluidos ideales”, suponiendo que la fricción entre las partículas de fluido frente a las fuerzas de inercia era despreciable, como en saltos de agua y, en general, en los flujos de alta velocidad.

Aunque fue un gran avance, por ejemplo, para calcular el movimiento lento de la miel, la ecuación de Euler falla, ya que la viscosidad del flujo (las fuerzas de fricción) tiene más importancia frente a las fuerzas inerciales. El mismo problema se produce en la resolución de los flujos en relación con los sólidos o obstáculos, ya que cerca del obstáculo se generan grandes gradientes de velocidad debido a las fuerzas de fricción. Frente a esto, en 1822 Claude-Louis Henri Navier y veinte años después George Gabriel Stokes añadieron a la ecuación de Euler la influencia del rozamiento del fluido viscoso o viscoso, formulando lo que hoy conocemos como ecuaciones de Navier-Stokes. A continuación se encuentran dos principios básicos aplicados a una partícula de fluidos: la conservación de la masa (ecuación de continuidad) y la segunda ley de Newton, que relaciona la tasa de crecimiento del momento de la partícula del fluido (a la izquierda de la ecuación) con las fuerzas de presión, gravedad y fricción que lo provocan (a la derecha de la ecuación).

En los rincones más oscuros de las matemáticas

Como es habitual, para llegar a la solución de ecuaciones diferenciales es necesario establecer condiciones iniciales. En este caso, debemos proporcionar a las ecuaciones de Navier-Stokes (una ecuación en cada dirección) una distribución de velocidad y presión del flujo en las tres dimensiones del espacio en un momento dado. A partir de ahí, las ecuaciones deberían devolver la velocidad y la presión del flujo en cualquier momento del futuro. ¿Qué supondría esto? Por ejemplo, seríamos capaces de predecir exactamente los fenómenos meteorológicos a lo largo del tiempo, de definir completamente el movimiento de las corrientes oceánicas y de las olas, de resolver con precisión la aerodinámica en torno a los cuerpos… Si esto fuera posible, probablemente, veríamos y entenderíamos la realidad de otra manera. Lamentablemente, transcurridos dos siglos, la solución analítica sólo se conoce para aquellos flujos que cumplen ciertas condiciones. Basta con fijarse en la ecuación de la causa: las derivadas parciales de segundo orden (en las fuerzas de rozamiento) y las no linealidades (en la aceleración convectiva) presentan enormes dificultades a la hora de resolver analíticamente las ecuaciones.

Aunque parezca mentira, desde el punto de vista de físicos e ingenieros, las ecuaciones pueden describir la realidad con total fiabilidad, ¿cómo es posible? Para ello se utiliza una herramienta matemática habitual: resolver ecuaciones mediante métodos numéricos, escribiendo cada término de la ecuación de forma algebraica y aplicando determinadas condiciones de contorno, obteniendo soluciones aproximadas.

A la izquierda: La distribución de temperatura en una llama de hidrógeno mediante el cálculo CFD, el espacio está formado por elementos discretos. Derecha: Imagen de la llama obtenida en las mediciones de laboratorio. Ed. Gontzal Lopez Ruiz

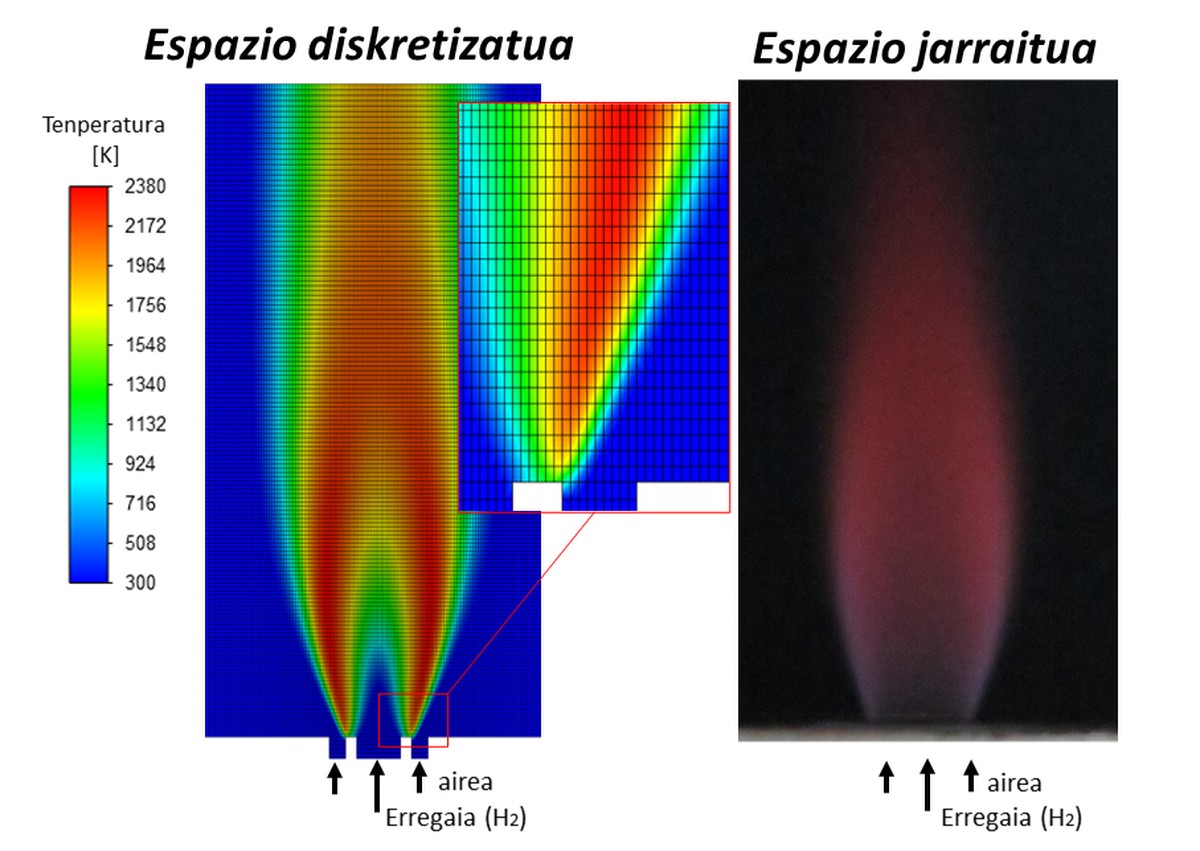
La disciplina conocida como “Computational Fluid Dynamics” o CFD, resuelve las ecuaciones de Navier-Stokes a través del álgebra de matrices en los flujos laminos y turbulentos. A pesar de que el coste del cálculo computacional puede ser muy elevado en función del problema planteado, en las últimas décadas esta herramienta de simulación ha cobrado fuerza en diversos ámbitos de la investigación y la industria. De hecho, el movimiento de los fluidos puede ir acompañado de la simulación de la transferencia de calor, las reacciones químicas o las deformaciones de los sólidos producidos por los fluidos, resolviendo problemas multi-físicos que se dan en la realidad. En el arte, los matemáticos trabajan para demostrar la existencia y la soledad de las soluciones.

¿Fuera de la realidad?

En 1933, el matemático Jean Leray demostró la existencia y soledad de las soluciones “débiles” de las ecuaciones considerando un pequeño intervalo de tiempo [3]. Sí, como se puede ver, simplificó mucho el problema. Frente a soluciones suaves, mediante una formulación débil se pueden encontrar soluciones no diferenciales que pueden presentar la ecuación, facilitando como punto de partida el aprendizaje de la existencia y la soledad de las ecuaciones. Este importante antecedente ha llevado a los matemáticos a adoptar una nueva posición ante el problema, según Tristan Buckmaster, de la Universidad Princeton, “una de las estrategias sería demostrar que las soluciones débiles de Leray son suaves, y si se consiguiera resolvería el problema del milenio” [2]. Soluciones suaves describirían completamente la realidad física, disponiendo de una solución en cada uno de los puntos del área considerados en cualquier momento (soluciones de zonas de velocidad y presión). La clave y la principal duda de los matemáticos es que al poner en marcha el cálculo considerando una formulación suave, se pueden obtener vectores de velocidad adecuados a lo largo del tiempo, pero es posible que de repente los resultados devuelvan la velocidad infinita en algún punto del campo: las ecuaciones han explosionado.

En este sentido, los últimos avances han intensificado sus dudas. En el artículo publicado en 2017 por los matemáticos Tristan Buckmaster y Vlad Vicol de la Universidad de Princeton [4], para ciertas definiciones de soluciones “débiles”, se cuestionó la soledad de las soluciones de Leray. Estos resultados permiten, a partir de unas condiciones iniciales, llegar a situaciones físicamente imposibles. No obstante, se plantean dudas sobre los resultados planteados en el artículo; es posible que las soluciones consideradas “débiles” incidan en el resultado final y exista una soledad para las soluciones “menos débiles”.

Necesidad de simulacros

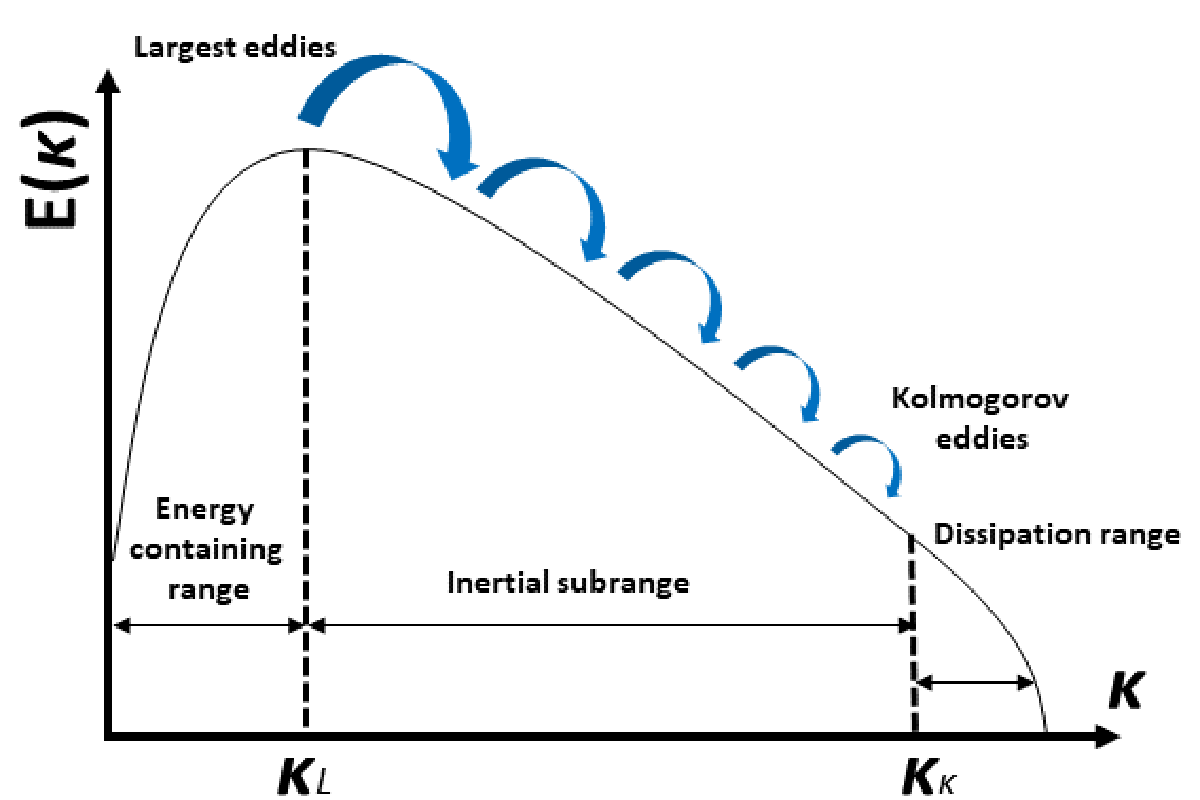
Como se ha comentado, los métodos numéricos y algoritmos desarrollados en las últimas décadas permiten resolver de forma aproximada las ecuaciones de Navier-stokes. Sin embargo, dentro de los cálculos CFD existen una serie de problemas cuyo principal reto es el desarrollo de modelos físicos adecuados para simular el flujo turbulento junto con otros fenómenos (reacciones de combustión, deformaciones de objetos, transferencia de calor). La característica principal de los flujos turbulentos es el movimiento caótico y desordenado de las partículas, formado por turbulencias a diferentes escalas. Por lo tanto, las trayectorias de las partículas de fluido sufren a lo largo del tiempo fuertes cambios de dirección y velocidad, dificultando el cálculo por métodos numéricos. Para comprender la relación de remolinos a diferentes tamaños o escalas se definió el espectro o escala de energía cinética turbulenta [5]. Según esta escala, los remolinos grandes transmiten energía cinética a través del espectro a los turbulentos menores de tamaño similar, llegando a escalas pequeñas y hasta que la viscosidad del fluido disipa los remolinos. Se puede decir que el espectro nos muestra la competencia entre las fuerzas de inercia y fricción.

Espectro de energía cinética turbulenta. Ed. Gontzal Lopez Ruiz

En base a este concepto se han desarrollado diferentes modelos en función del tamaño de torbellino que se pretende resolver. Por ejemplo, resolver toda la escala mediante métodos numéricos en los puntos del espacio considerado (conocido como Direct Navier-Stokes o DNS) es un lujo al alcance de unos pocos, ya que para resolver los tiempos y espacios tan pequeños en las turbulencias más pequeñas es necesario utilizar cálculos por super-computador. Con el fin de reducir el coste computacional, los modelos turbulentos más habituales establecen filtros a escala, resolviendo una parte (turbulentos elevados) y modelando otra (turbulencias menores). En los últimos años esta técnica, conocida como Large Eddy Simulation o LES, ha tomado fuerza en la investigación de problemas físicos y en el desarrollo de diseños dirigidos a diferentes sectores.

Prototipo de estudio de ventilación de viviendas: Experimentos en túnel de viento y simulaciones LES. Ed. T. van Hoof y colaboradores [6] - CC BY NC ND

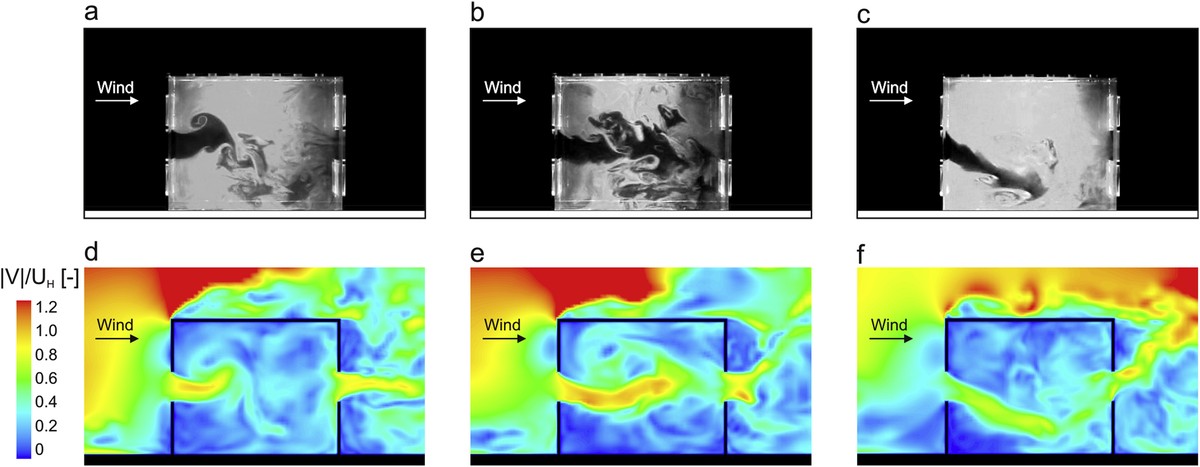
Aunque esperamos resolver la realidad a través de estas ecuaciones, no debemos olvidar que las ecuaciones diferenciales son aproximaciones generadas por el hombre. El premio del Instituto de Matemáticas Clay tendrá que esperar a que el trabajo continuo de los matemáticos dé resultados claros. Además, con el objetivo de reducir el coste computacional y mejorar la precisión de soluciones aproximadas mediante métodos numéricos, los investigadores trabajan en este campo de la ciencia en desarrollo. La frase que ponen en boca del físico Werner Heisenberg resume bien la magnitud del reto: “Cuando me encuentro con Dios le voy a hacer dos preguntas: ¿Por qué la relatividad? ¿Y por qué la turbulencia? Estoy seguro de que tendrá respuesta a la primera pregunta”.

BIBLIOGRAFÍA:

[1] Fefferman C. 2006. “Existence and smoothness of the Navier-Stokes equation”, Millennium Prize Problems, Clay Math. Inst., Cambridge, MA, 2006, 57-67, URL: https://www.claymath.org/sites/default/files/navierstokes.pdf

2] K. Hartnett 2017 Mathematicians Find Wrinkle in Famed Fluid Equations. Quantamagazine. URL: https://www.quantamagazine.org/mathematicians-find-wrinkle-in-famed-fluid-equations-20171221/

[3] Leray J. 1934. “Sur le mouvement d’un liquide visqueux emplissant l’espace”. Acta Math., 63(1), 193–248.

[4] Buckmaster T. y Vicol V. 2019. “Nonuniqual of weak solutions to the Navier-Stokes equation”. Ann. of Math. (2) 189 (2019), no. 1, 101–144.

[5] Kolmogorov A.N. 1941. “Dissipation of energy in locally isotropic turbulence”. Doc. Acad. Nau. SSSR, 32, 16-18.

[6] van Hooff T., B. de Block y Tominaga Y. 2017 “On the accuracy of CFD simulations of cross-ventilation flows for a generic isolated building: Comparison of RANS, LES and experiments”. Building and Environment, 114, 148-165.