NAVIER-STOKES: pris dans le tourbillon de questions

Friction, origine des casseroles de tête

Flux sanguin à travers les artères du cœur, mouvement des courants et nuages d'air atmosphérique, ou flux autour des pales d'un avion: nous pouvons former une liste interminable de phénomènes physiques liés à la dynamique des fluides. De la main des grands noms de la physique et les mathématiques, tout au long de l'histoire ont été nombreux efforts pour comprendre et prévoir ces phénomènes. Comme on pouvait s’y attendre, nous devons aller au domaine des lumières pour trouver les premières esquisses des équations différentielles qui décrivent la dynamique des fluides « idéaux ». En particulier, en 1755 Leonhard Euler a présenté l'équation différentielle des «fluides idéaux», en supposant que la friction entre les particules de fluide par rapport aux forces d'inertie était négligeable, comme dans les sauts d'eau et, en général, dans les flux à grande vitesse.

Bien que ce soit une avancée majeure, par exemple, pour calculer le mouvement lent du miel, l'équation d'Euler échoue, car la viscosité du flux (les forces de friction) a plus d'importance face aux forces inertielles. Le même problème se produit dans la résolution des flux par rapport aux solides ou aux obstacles, car près de l'obstacle, de grands gradients de vitesse sont générés en raison des forces de friction. Face à cela, en 1822 Claude-Louis Henri Navier et vingt ans plus tard George Gabriel Stokes ajoutèrent à l'équation d'Euler l'influence du frottement du fluide visqueux ou visqueux, formulant ce que nous connaissons aujourd'hui comme des équations de Navier-Stokes. Voici deux principes de base appliqués à une particule de fluides : la conservation de la masse (équation de continuité) et la seconde loi de Newton, qui relie le taux de croissance du moment de la particule du fluide (à gauche de l'équation) aux forces de pression, de gravité et de friction qui le provoquent (à droite de l'équation).

Dans les coins les plus sombres des mathématiques

Comme d'habitude, pour parvenir à la solution des équations différentielles, il est nécessaire d'établir des conditions initiales. Dans ce cas, nous devons fournir aux équations de Navier-Stokes (une équation dans chaque direction) une distribution de vitesse et de pression du flux dans les trois dimensions de l'espace à un moment donné. À partir de là, les équations devraient retourner la vitesse et la pression du flux à tout moment dans le futur. Que supposerait cela ? Par exemple, nous serions capables de prédire exactement les phénomènes météorologiques au fil du temps, de définir complètement le mouvement des courants océaniques et des vagues, de résoudre avec précision l'aérodynamique autour des corps… Si cela était possible, nous verrions et comprendrions probablement la réalité autrement. Malheureusement, après deux siècles, la solution analytique n'est connue que pour les flux qui remplissent certaines conditions. Il suffit de se fixer sur l'équation de la cause: les dérivées partielles du second ordre (dans les forces de friction) et les non-linéarités (dans l'accélération convective) présentent d'énormes difficultés à résoudre analytiquement les équations.

Même s'il semble mensonger, du point de vue des physiciens et des ingénieurs, les équations peuvent décrire la réalité avec une fiabilité totale, comment est-ce possible ? Pour cela, on utilise un outil mathématique habituel: résoudre les équations par des méthodes numériques, en écrivant chaque terme de l'équation de manière algébrique et en appliquant certaines conditions de contour, en obtenant des solutions approximatives.

À gauche : La distribution de température dans une flamme d'hydrogène par le calcul CFD, l'espace est constitué d'éléments discrets. A droite : Image de la flamme obtenue dans les mesures de laboratoire. Ed. Gontzal Lopez Ruiz

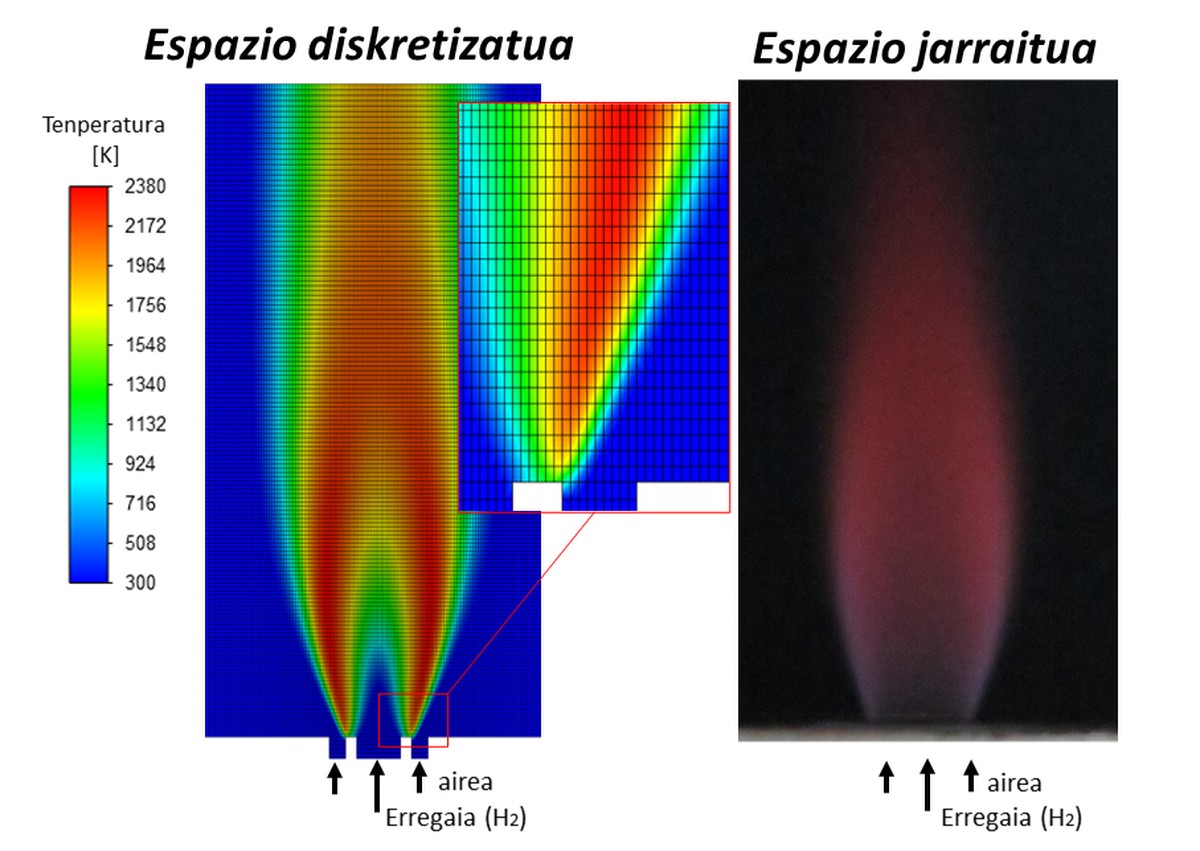
La discipline connue sous le nom de « Computational Fluid Dynamics » ou CFD, résout les équations de Navier-Stokes par l'algèbre des matrices dans les flux laminés et turbulents. Bien que le coût du calcul puisse être très élevé en fonction du problème posé, ces dernières décennies, cet outil de simulation a pris de la force dans divers domaines de la recherche et de l'industrie. En effet, le mouvement des fluides peut être accompagné de la simulation du transfert de chaleur, des réactions chimiques ou des déformations des solides produits par les fluides, en résolvant des problèmes multi-physiques qui se donnent dans la réalité. Dans l'art, les mathématiciens travaillent à démontrer l'existence et la solitude des solutions.

En dehors de la réalité ?

En 1933, le mathématicien Jean Leray a démontré l'existence et la solitude des solutions «faibles» des équations en considérant un petit intervalle de temps [3]. Oui, comme vous pouvez le voir, il a beaucoup simplifié le problème. Face à des solutions douces, par une formulation faible, on peut trouver des solutions non différentielles qui peuvent présenter l'équation, facilitant comme point de départ l'apprentissage de l'existence et la solitude des équations. Cet important antécédent a conduit les mathématiciens à adopter une nouvelle position face au problème, selon Tristan Buckmaster, de l’Université Princeton, «une des stratégies serait de démontrer que les solutions faibles de Leray sont douces, et si on réussissait à résoudre le problème du millénaire» [2]. Des solutions douces décriraient complètement la réalité physique, disposant d'une solution à chacun des points de la zone considérés à tout moment (solutions de zones de vitesse et de pression). La clé et le principal doute des mathématiciens est qu'en lançant le calcul en considérant une formulation douce, vous pouvez obtenir des vecteurs de vitesse appropriés au fil du temps, mais il est possible que soudain les résultats retournent la vitesse infinie à un certain point du champ: les équations ont explosé.

En ce sens, les derniers développements ont intensifié leurs doutes. Dans l'article publié en 2017 par les mathématiciens Tristan Buckmaster et Vlad Vicol de l'Université de Princeton [4], pour certaines définitions de solutions «faibles», on a remis en question la solitude des solutions de Leray. Ces résultats permettent, à partir de conditions initiales, de parvenir à des situations physiquement impossibles. Cependant, des doutes sont soulevés sur les résultats présentés dans l’article; il est possible que les solutions considérées comme «faibles» incitent au résultat final et qu’il existe une solitude pour les solutions «moins faibles».

Besoin de simulations

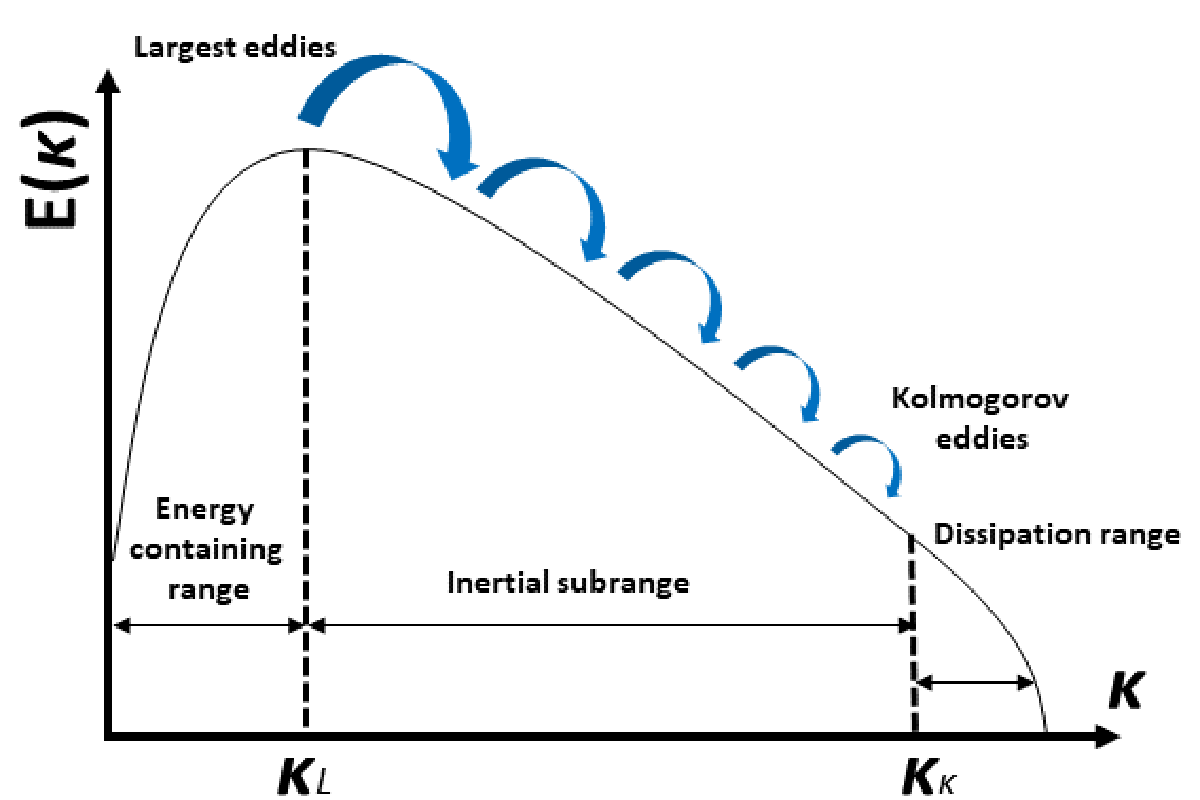
Comme mentionné, les méthodes numériques et les algorithmes développés au cours des dernières décennies permettent de résoudre approximativement les équations de Navier-stokes. Cependant, dans les calculs CFD il existe un certain nombre de problèmes dont le principal défi est le développement de modèles physiques appropriés pour simuler le flux turbulent avec d'autres phénomènes (réactions de combustion, déformations d'objets, transfert de chaleur). La caractéristique principale des flux turbulents est le mouvement chaotique et désordonné des particules, formé par des turbulences à différentes échelles. Par conséquent, les trajectoires des particules de fluide subissent au fil du temps de forts changements de direction et de vitesse, rendant difficile le calcul par des méthodes numériques. Pour comprendre le rapport de tourbillons à différentes tailles ou échelles, on a défini le spectre ou l'échelle d'énergie cinétique turbulente [5]. Selon cette échelle, les grandes tourbillons transmettent de l'énergie cinétique à travers le spectre aux turbulents mineurs de taille similaire, atteignant de petites échelles et jusqu'à ce que la viscosité du fluide dissipe les tourbillons. On peut dire que le spectre nous montre la concurrence entre les forces d'inertie et de friction.

Spectre d'énergie cinétique turbulent. Ed. Gontzal Lopez Ruiz

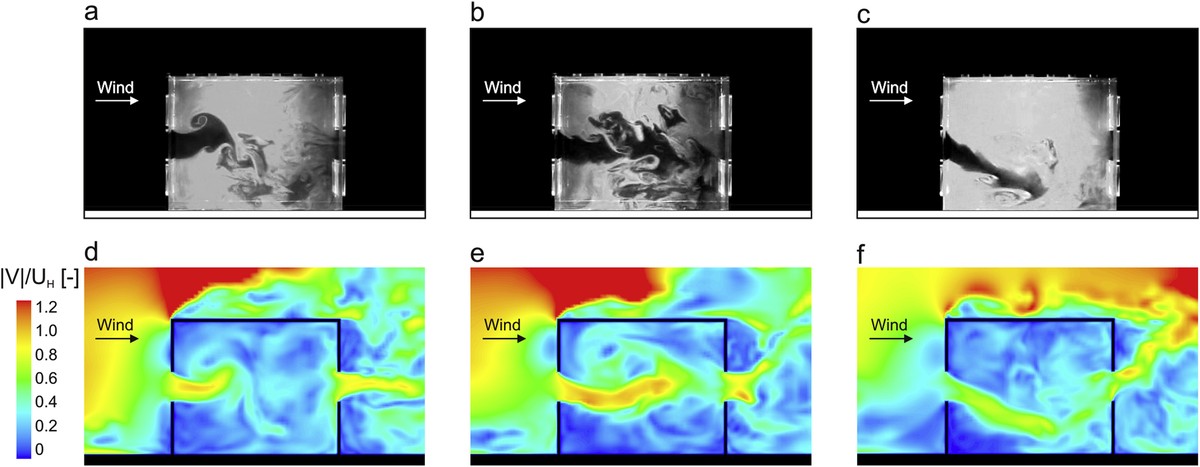
Sur la base de ce concept, différents modèles ont été développés en fonction de la taille de tourbillon qui est destiné à être résolu. Par exemple, résoudre toute l'échelle par des méthodes numériques dans les points de l'espace considéré (connu sous le nom de Direct Navier-Stokes ou DNS) est un luxe à portée de quelques-uns, car pour résoudre les temps et les espaces si petits dans les plus petites turbulences, il est nécessaire d'utiliser des calculs par super-ordinateur. Afin de réduire le coût informatique, les modèles turbulents les plus courants établissent des filtres à échelle, en résolvant une partie (turbulences élevées) et en modélisant une autre (turbulences mineures). Ces dernières années, cette technique, connue sous le nom de Large Eddy Simulation ou LES, a pris de l'ampleur dans la recherche de problèmes physiques et dans le développement de conceptions destinées à différents secteurs.

Prototype d'étude de ventilation de logement: Expériences en soufflerie et simulations LES. Ed. T. van Hoof et collaborateurs [6] - CC BY NC ND

Bien que nous espérons résoudre la réalité à travers ces équations, nous ne devons pas oublier que les équations différentielles sont des approximations générées par l'homme. Le prix de l'Institut de mathématiques Clay devra attendre que le travail continu des mathématiciens donne des résultats clairs. En outre, afin de réduire les coûts informatiques et d'améliorer la précision des solutions approximatives par des méthodes numériques, les chercheurs travaillent dans ce domaine de la science en développement. La phrase qu’ils mettent dans la bouche du physicien Werner Heisenberg résume bien l’ampleur du défi: « Quand je rencontre Dieu, je vais lui poser deux questions : Pourquoi la relativité? Et pourquoi la turbulence? Je suis sûr que vous aurez une réponse à la première question.»

BIBLIOGRAPHIE:

[1] Fefferman C. 2006. “Existence et smoothness of the Navier-Stokes equation”, Millennium Prize Problems, Clay Math. Inst., Cambridge, MA, 2006, 57-67, URL: https://www.claymath.org/sites/default/files/navierstokes.pdf

2] K. Hartnett 2017 Mathematicians Find Wrinkle in Famed Fluid Equations. Quantamagazine. URL: https://www.quantamagazine.org/mathematicians-find-wrinkle-in-famed-fluid-equations-20171221/

[3] Leray J. 1934. “Sur le mouvement d’un liquide visqueux emplissant l’espace”. Acta Math., 63(1), 193-248.

[4] Buckmaster T. et Vicol V. 2019. “Nonuniqual of weak solutions to the Navier-Stokes equation”. Ann. Of Math. (2) 189 (2019), non. 1, 101–144.

[5] Kolmogorov A.N. 1941. “Dissipation of energy in locally isotropic turbulence”. Doc. Acad. Nau. SSSR, 32, 16-18.

[6] van Hooff T., B. de Block et Tominaga Y. 2017 “On the accuracy of CFD simulations of cross-ventilation flows for a generic isolated building: Comparison of RANS, LES and experiments”. Building and Environment, 114, 148-165.