Bailando con electrones para iluminar la nanoescala
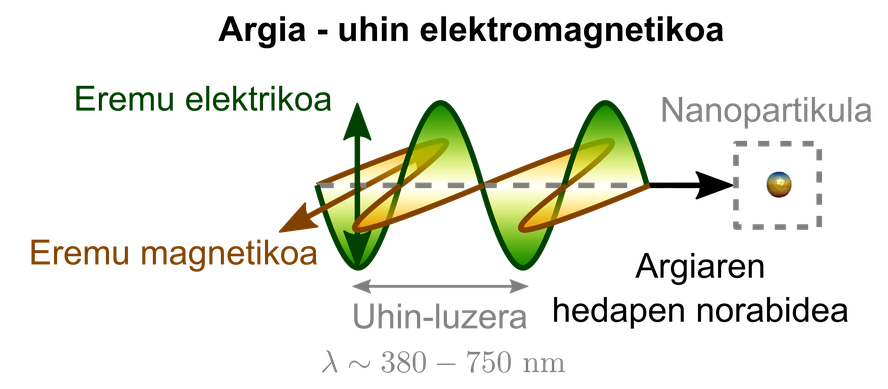
Muchos de los avances tecnológicos y descubrimientos científicos realizados a lo largo de la historia se han basado en la mejora de nuestra capacidad visual. XVI. y XVII. durante siglos, las invenciones de la lupa y, especialmente, de los primeros microscopios ópticos dieron un notable impulso a la biología y a la medicina. Estos sistemas ópticos tradicionales, sin embargo, tienen una resolución limitada, es decir, soportan una difracción que permite caracterizar aquellos detalles que poseen un tamaño de onda de luz similar o superior a la longitud de onda de la luz utilizada. La longitud de onda es la distancia de dos onda geminadas, como se muestra en la figura 1. En el caso de las olas del mar, por ejemplo, la distancia entre las cumbres suele ser de unas decenas de metros. En el caso de la luz visible, por el contrario, la longitud de onda oscila entre los 380 nm y los 750 nm, por lo que no es posible distinguir detalles de menor tamaño utilizando sistemas ópticos tradicionales.
Para superar el límite que impone la difracción, necesitamos técnicas que permitan confinar la luz en un espacio que es menor que su longitud de onda. Afortunadamente, la interacción de la luz y la materia en la nanoescala puede dar lugar a la localización de la luz en esta escala. Para ello hay que sumergirnos en el reino de la nanofotónica.
Bailando con electrones
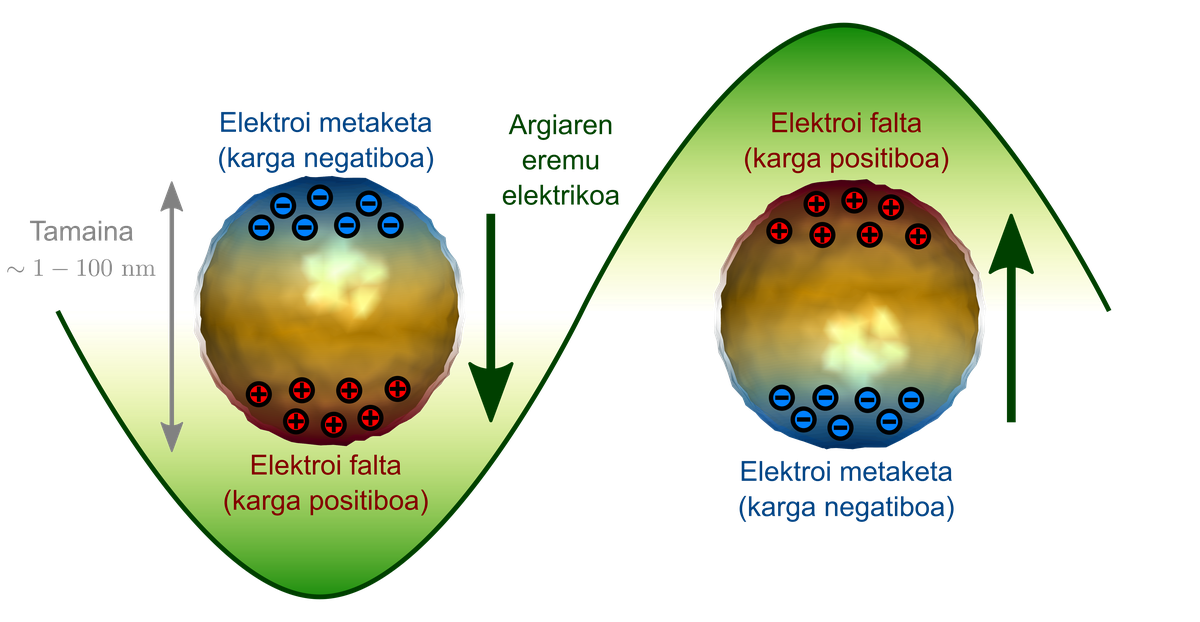
El confinamiento subyacente a la longitud de onda de la luz puede conseguirse, entre otras cosas, mediante plasmones superficiales. ¿Qué son los plasmones? En los materiales conductores, a diferencia de los aislantes, los electrones pueden moverse libremente. El conjunto de electrones libres se puede representar como un gas o una nube. Si esta nube sale de su estado de equilibrio —2. tal y como se muestra en la figura, falta de electrones en el lugar en el que se encontraba al principio. En un punto tendremos, por tanto, un excedente de carga negativa y, por otro lado, un exceso de carga positiva en la región en la que estaban situados estos electrones. Debido a la atracción de cargas positivas y negativas entre sí, el electrón-nube soportará una fuerza de atracción que oscilará de un lado a otro con una frecuencia propia. Es decir, los electrones pueden bailar en los materiales conductores, y para ello tienen un ritmo propio que depende del material. Estas oscilaciones colectivas de electrones libres se denominan plasmois.
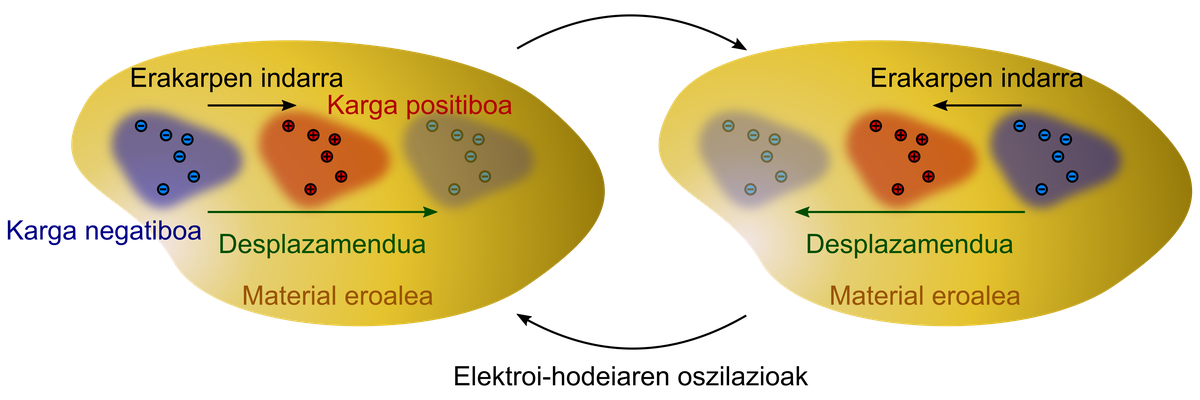
Los plasmones pueden excitarse mediante la luz y, en general, mediante ondas electromagnéticas. En una estructura cerrada y conductora, como una nanopartícula, los electrones locales seguirán el campo eléctrico de esa onda y se acumularán en un lado de la superficie de la nanopartícula, como se muestra en la figura 3. A medida que el campo eléctrico de la luz oscila, el electrón-nube también oscilará siguiendo él, bailando al ritmo que marca la luz. Si la frecuencia de la luz es igual a la frecuencia natural, tendremos una resonancia en la nanopartícula, es decir, excitaremos un plasmón.
Una acumulación de cargas que tenemos en superficie generará un campo eléctrico que se denomina zona inducida. Este campo eléctrico inducido es muy violento alrededor de la superficie donde se ha depositado la carga. La intensidad de la luz iluminada puede ser hasta 100 veces más intensa que la que hemos utilizado, pero se debilita muy rápidamente (exponencialmente) a medida que nos alejamos de la superficie. Esto nos permite tener una ampliación del campo en una región de unos pocos nanómetros. En consecuencia, los plasmones tienen la capacidad de localizar la luz y pueden aprovecharse para superar el límite de difracción. Esto permite diferenciar detalles próximos a la superficie de la nanopartícula, como moléculas. ¡Quién pensaría que algunos bailarines de electrones podían aclarar la nanoescala!
No sólo eso, las nanopartículas plasmónicas tienen la capacidad de localizar la luz en la nanoescala, sino también de dispersar la luz a distancia. Es decir, como una antena, tienen la capacidad de recibir y emitir después ondas electromagnéticas: son las nanoantenas. Esta capacidad nos permite interrogar nanopartículas plasmónicas utilizando la luz para obtener información sobre la nanopartícula y su entorno.
La localización de la luz al límite
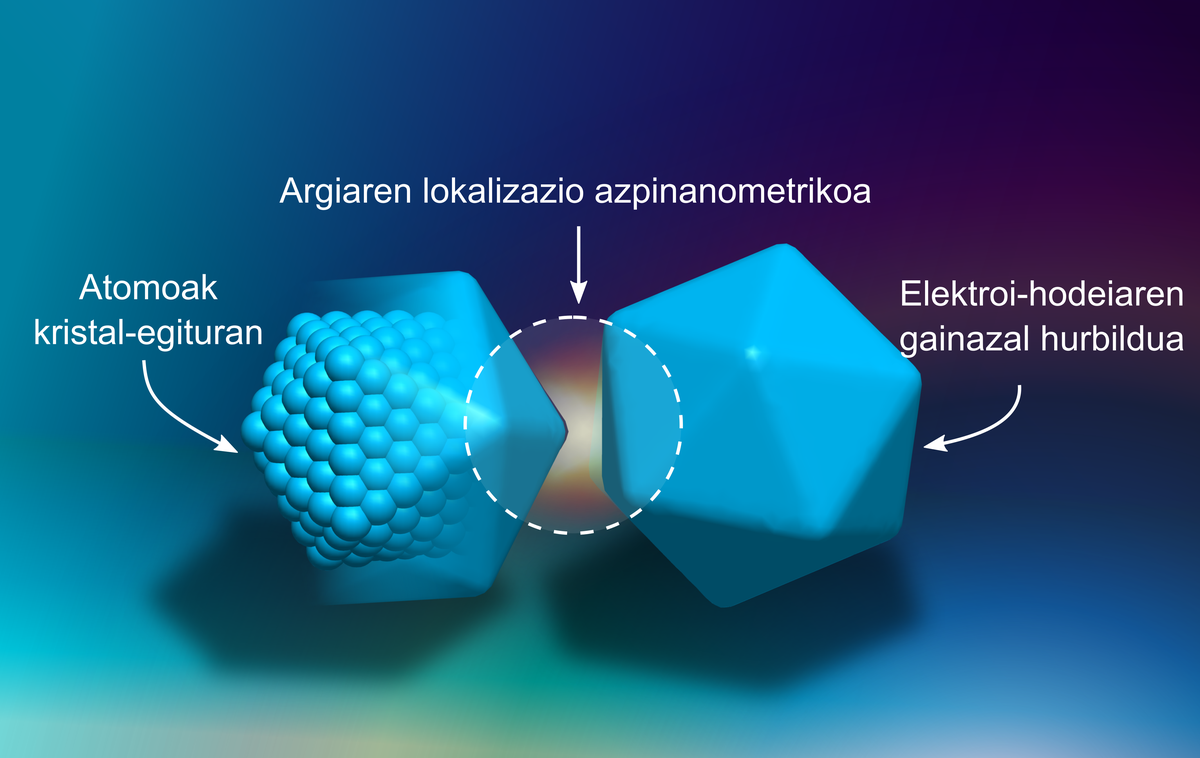
Los plasmones excitables en las nanopartículas presentan una dependencia de cuatro características: tamaño, geometría, material y medio de la misma. En mi tesis he estudiado la influencia de la geometría de las nanopartículas en los campos inducidos. De hecho, alrededor de los vértices se localiza aún más el campo eléctrico en los conductores, ya que allí se acumulan más electrones. Este fenómeno se denomina efecto pararrayos (el funcionamiento de los pararrayos se basa en este fenómeno).
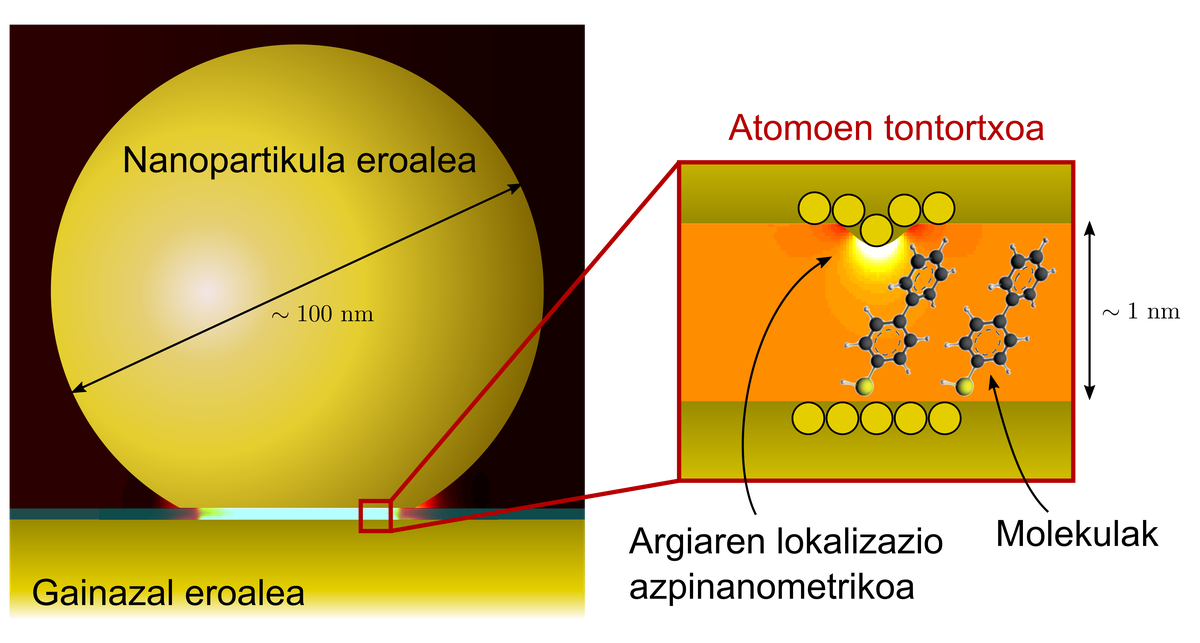
He visto en mi tesis que el comportamiento de los electrones a escala atómica es similar. Su combinación con plasmones permite la localización subanométrica de la luz. Esta localización subanométrica de la luz proporciona información sobre un espacio muy reducido, como se muestra en la figura 4. Por ejemplo, si tenemos moléculas entre nanopartículas y superficies conductoras, podemos excitar las vibraciones de estas últimas y estudiar su estructura. ¡Sí, las moléculas también pueden bailar!
Elementos necesarios para predecir la localización de la luz
Para predecir, mediante simulación, la localización del campo que podemos obtener en los vértices de una nanopartícula o nanoestructura de estas características, podemos utilizar diferentes modelos. De hecho, habría que partir de un modelo que tenga en cuenta la posición de los átomos, es decir, la estructura cristalina. No sólo eso, sino también el carácter cuántico de los electrones. Sin embargo, en esta tesis hemos utilizado modelos más sencillos para predecir la localización del campo y la cuantía de la ampliación. La forma o forma de la nube electrón-sin excitación externa, es decir, sin iluminación, puede ser suficiente en muchos casos. La figura 5 muestra dos ejemplos. Es decir, no es imprescindible describir detalladamente la estructura cristalina. A la sala de fiestas se le han colocado muros, teniendo en cuenta el espacio que utilizan los electrones para bailar, de forma que el ritmo de la música y los movimientos de los bailarines no sufran cambios significativos.
En lugar de utilizar luz para analizar muestras y excitar plasmones, podemos utilizar otras técnicas. Se pueden utilizar los electrónes, por ejemplo, utilizando microscopios electrónicos de barrido y transmisión. Este tipo de microscopios lanzan electrón-haz para recoger las muestras tras colisionar o atravesarlas. De esta forma se miden parámetros como la energía que han perdido los electrónes, el desvío que han sufrido. Estos datos permiten analizar las propiedades de la muestra. Además, se consigue una resolución mucho mejor que con la luz y se permite una resolución por debajo de los nanómetros. Los electrónes también pueden usarse para excitar plasmones en nanoestructuras conductoras. Por su resolución los electrónes son más sensibles que las técnicas que utilizan la luz sobre la geometría de la nanopartícula. Una oportunidad única para definir los límites de los modelos. Como he demostrado en mi tesis, la descripción detallada de la geometría de la nanopartícula en los modelos simples mencionados es imprescindible para confirmar los resultados que se obtienen en modelos más complejos.
La apreciación de la geometría de forma más o menos aproximada facilita considerablemente las simulaciones. Es más, muchas de las nanoestructuras utilizadas en muchos experimentos son demasiado grandes y complejas para poder tener en cuenta los átomos uno a uno y así realizar simulaciones por ordenador. Simplemente, los ordenadores actuales no disponen de la suficiente potencia para realizar los pesados cálculos de los mismos. Es necesario, por tanto, determinar las limitaciones y capacidades de los modelos más sencillos disponibles para confirmar la fiabilidad de los resultados y previsiones obtenidos en los simulacros. No le tenemos que dar a la hora de bailar con los electrones perdidos.
BIBLIOGRAFÍA
L. Novotny and B. Hecht, “Principles of Nano-Optics”, Cambridge University Press, Cambridge, 2012.
P. N. Prasad, “Nanophotonics”, John Wiley & Sons, Inc., Hoboken, NJ, 2004.
M. Pelton, J. Aizpurua y G. Bryant, “Metal-nanoparticle plasmonics”, Laser & Photonics Review 2, 136–159 (2008).
F. Benz, M. C. Schmidt, A. Dreismann, R. Chikkaraddy, Y. Zhang, A. Demetriadou, C. Carnegie, H. Ohadi, B. de Nijs, R. Esteban, J. Aizpurua y J. J. Baumberg, “Single-molecule optomechanics in “picocavities”, Science 354, 726–729 (2016).
M. Urbieta, M. Barbry, Y. Zhang, P. Koval, D. Sánchez - Portal, N. Zabala y J. Aizpurua, “Atomic-Scale Lightning Rod Effect in Plasmonic Picocavities: A Classical View to a Quantum Effect”, ACS Nano 12, 585–595 (2018)
R. Egerton, “Electron Energy -Loss Spectroscopy in the Electron Microscope”. Springer US, Boston, MA, 2011.
F. J. García De Abajo, “Optical excitations in electron microscopy”, Reviews of Modern Physics 82, 209–275 (2010).