Hasiera »   Gai librean »   Ekuazio diferentzialak egonkortasun bila

Ecuacións diferenciais en busca de estabilidade

• Zabaldu:
• Twitter
• Facebook
• Emaila

A estabilidade é un tesouro prezado. A vida é una procura constante de estabilidade: procura dun traballo fixo, dunha relación forte e longa, etc. Aínda que sexan variables, adóitase denominar estable a aquel que se atopa dentro de parámetros que non presentan cambios bruscos. Sinónimo de aburrimento paira algúns, un tesouro desexado en xeral.

Tamén en matemáticas hai disciplinas nas que a estabilidade é fundamental. Os que queremos fixarnos teñen cabida nos programas das carreiras científicas e técnicas, utilízanse na formulación de modelos matemáticos e paira algúns se busca un resultado analítico, mentres que outros se resolven con métodos numéricos --aproximacións - e co computador como acompañante. A algúns alumnos gústalles, pero á maioría cáusanlles quebradizos de cabeza. Que son? Son ecuacións diferenciais. As ecuacións diferenciais, do mesmo xeito que o ser humano na vida, buscan o maior campo de estabilidade posible.

Utilidade das ecuacións diferenciais

Un modelo matemático é un dispositivo que describe un sistema ou suceso da vida. A formulación dun modelo matemático comeza coa identificación das variables que inflúen no sistema, é dicir, producen un cambio no sistema. A continuación establécense hipóteses razoables sobre o sistema, identificando as leis empíricas aplicables. Algunhas destas hipóteses indican a medida da variación dalgunhas das variables previamente definidas. O enunciado matemático destas hipóteses será una ecuación ou un sistema de ecuacións no que aparezan as derivadas, que é o sistema de ecuacións diferenciais.

A súa resolución concreta permitiranos coñecer o comportamento do sistema. Pero, de que falamos cando falamos de modelo ou modelo matemático?

Na cinética das reaccións químicas interesa a súa evolución ao longo do tempo. Ao ser as velocidades derivadas do tempo de calquera variable, a cinética das reaccións se modeliza mediante ecuacións diferenciais. Exemplo diso é o caso de que ambas as sustancias xeran un terceiro. As variables son concentracións de sustancias, mentres que as leis empíricas son a lei de acción de masas e a lei de conservación de masas. A primeira dinos que o produto das concentracións dos reactivos é proporcional ao produto das concentracións dos produtos, e as segundas, a suma das masas dos reactivos é igual á dos produtos.

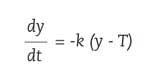
Na refrixeración dos corpos tamén se utilizan ecuacións diferenciais. Por exemplo, se sacamos un pastel do forno a 150ºC e queremos saber a súa temperatura en calquera momento. Se estamos a investigar o homicidio ou o asasinato dunha persoa e queremos calcular a que hora morreu, utilizaremos a lei de refrixeración de Newton. Esta lei establece que o cambio de temperatura da superficie corporal é proporcional á diferenza entre a temperatura corporal e a temperatura ambiente. Así, se a temperatura do corpo no instante t é e ( t ) e a temperatura no medio T, segundo a lei de Newton, cumprirase a seguinte ecuación diferencial:

sendo k 0 a proporcionalidade constante.

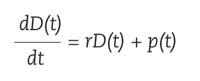
Queremos calcular os intereses que nos dará una cantidade de diñeiro que ingresamos no banco? Deberemos utilizar ecuacións diferenciais. Supoñamos que introducimos no banco a cantidade D 0 e págannos un tipo de interese r. Chamaremos D ( t ) á cantidade que teremos dentro de t anos. A variación da cantidade será a suma da variación por acumulación de intereses e a variación de ingresos que realizamos no banco, p de fórmula.

Hai, por tanto, que modelar na vida cotiá utilizando ecuacións diferenciais.

Dificultades de resolución

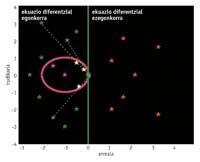
Una vez obtida a ecuación diferencial débese resolver. En ocasións, non é posible a súa liberación analítica, e mediante métodos numéricos obtense un resultado aproximado. As ecuacións diferenciais inclúen uns autovalores complexos que denominaremos l. Cando a parte real destes autovalores é positiva, a ecuación diferencial é inestable e o resultado aproximado que obteriamos utilizando un método numérico paira a súa liberación non ten por que parecerse á solución real, xa que un pequeno cambio ten un forte impacto neles. Por iso, os métodos numéricos aplícanse a ecuacións diferenciais estables, autobalioides de parte real negativa. Por outra banda, o propio método tamén ten una zona de estabilidade. E si quérese conseguir un bo resultado, os autovalores deben situarse alí. Por tanto, os autovalores das ecuacións diferenciais estables non presentes nesta zona trasládanse á zona de estabilidade, multiplicando os autovalores por un número h medido (0,1) que denominaremos medida do paso.

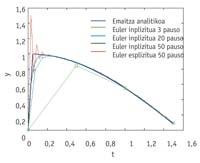
A medida do paso é fundamental paira resolver a ecuación e, por suposto, non pode ser calquera número. En termos de fiabilidade, o método de resolución debe ser o suficientemente pequeno como paira manterse dentro da zona de estabilidade e o suficientemente grande como paira dar o menor número de pasos posibles de face ao traballo. Como conseguir ese equilibrio?

Equilibrio da área de estabilidade

Paira saber que pasos pódense dar no método numérico hai que fixarse no erro. Ao utilizar métodos numéricos xérase un erro local en cada paso. Pero hai outro erro que aparece na lonxitude, que é a reprodución dos erros de cada paso, e que está formado polas potencias dun número chamado factor de amplificación. Paira evitar o aumento do erro, o factor de amplificación debe ser menor que a unidade. A zona que cumpre esta condición é a coñecida como zona de estabilidade do método. Pois ben, o autovalor l debe estar na zona de estabilidade tras multiplicarse por h para que o factor de amplificación sexa menor que a unidade. Pero non só iso, una vez que o produto l .h atópase na zona de estabilidade, vese si o número h debe ser menor, xa que calquera número que sexa menor que h que atopamos fai posible que despois de multiplicar o autovalor leve á zona. Dos números que permiten levar o autovalor ao campo, o número h que mantén o erro local dentro de una tolerancia é o que se elixe como medida do paso. Esta medida de paso permite ter controlados os dous erros (local e longitudinal). Canto maior sexa este número, maior será o número de pasos que poderemos dar e máis rápido será o resultado, un obxectivo que o gran campo de estabilidade permite alcanzar.

Pero a medida da zona de estabilidade tamén está condicionada. Depende da orde. A orde é o parámetro que se utiliza paira medir a precisión do método e é máis preciso canto máis alto é a orde. Normalmente, a medida que aumenta a orde, a zona de estabilidade diminúe. Isto obríganos a dar pasos menores, aínda que o resultado sexa máis preciso.

O propio método tamén condiciona a medida da zona de estabilidade. Os métodos implícitos adoitan ter unha área de estabilidade maior que os explícitos, pero tamén presentan desvantaxes: a principal é que se requiren operacións máis ou menos complexas que nos métodos explícitos. Por iso, cando os autovalores non son moi grandes, prefírese o método explícito, xa que as operacións a realizar serán máis sustentables.

O soño sería atopar a máxima estabilidade en ordes altas e métodos explícitos, pero tampouco neste campo da ciencia hai rareza. Co fin de conseguir que as ecuacións diferenciais sóltense facilmente por métodos numéricos, son numerosos os traballos realizados paira aumentar o campo de estabilidade. Os primeiros son os métodos de Adams Bashforth e Moulton, nos que se utiliza tanto a información do último paso como a información doutros pasos máis rápidos paira construír o seguinte paso. Desta forma conseguiuse subir a orde do método numérico, e o de orde 1 ten un campo maior que o de Euler explícito (tamén de orde 1). Una das propostas máis importantes foi a denominada BDF (fórmula backward differentiation) realizada por Gear cara a 1971, un método implícito que utilizaba información en varios pasos máis lixeiros. O método BDF conseguiu que as zonas de estabilidade fosen tamén importantes en ordes elevadas. Ultimamente predominan os métodos que utilizan a derivada 2 ou os chamados puntos de superfuturo, xa que teñen grandes áreas de estabilidade, aínda que incrementan o traballo a realizar en cada paso.

Moitos pequenos pasos ou poucos grandes pasos, aí está a clave. Nesta competencia, a primeira opción, con moitos pequenos pasos, ten a vantaxe da fiabilidade e a segunda a optimización do traballo. Unificar ambas as opcións nunha soa ocasión sería excelente, xa que se conseguiría "fiabilidade sen traballo excesivo". A clave paira romper este equilibrio radica en métodos de gran campo de estabilidade, que non pon límites tan ríxidos á medida do paso. Por iso é posible dar pasos non tan fiables e grandes pasos fiables.