Équations différentielles à la recherche de stabilité

Utilité des équations différentielles
Un modèle mathématique est un dispositif décrivant un système ou un événement de la vie. La formulation d'un modèle mathématique commence par l'identification des variables qui influencent le système, c'est à dire produire un changement dans le système. Voici des hypothèses raisonnables sur le système, identifiant les lois empiriques applicables. Certaines de ces hypothèses indiquent la mesure de la variation de certaines variables précédemment définies. L'énoncé mathématique de ces hypothèses sera une équation ou un système d'équations dans lequel les dérivées apparaissent, qui est le système d'équations différentielles.
Sa résolution concrète nous permettra de connaître le comportement du système. Mais de quoi parlons-nous quand on parle de modèle ou de modèle mathématique ?
Dans la cinétique des réactions chimiques, il intéresse son évolution au fil du temps. Étant les vitesses dérivées du temps de toute variable, la cinétique des réactions est modélisée par des équations différentielles. Par exemple, les deux substances génèrent un tiers. Les variables sont des concentrations de substances, tandis que les lois empiriques sont la loi d'action de masse et la loi de conservation de masse. La première nous dit que le produit des concentrations des réactifs est proportionnel au produit des concentrations des produits, et la seconde, la somme des masses des réactifs est égale à celle des produits.
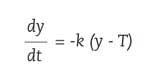
Dans le refroidissement des corps sont également utilisés équations différentielles. Par exemple, si nous sortons un gâteau du four à 150ºC et que nous voulons connaître sa température à tout moment. Si nous enquêtons sur le meurtre ou l'assassinat d'une personne et que nous voulons calculer à quelle heure elle est morte, nous utiliserons la loi de réfrigération de Newton. Cette loi stipule que le changement de température de la surface corporelle est proportionnel à la différence entre la température corporelle et la température ambiante. Ainsi, si la température du corps dans l'instant t est et ( t ) et la température dans le milieu T, selon la loi de Newton, la prochaine équation différentielle sera remplie:
étant k 0 la proportionnalité constante.
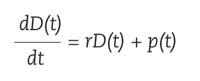
Voulons-nous calculer les intérêts qui nous donneront un montant d'argent que nous entrons dans la banque? Nous devrons utiliser des équations différentielles. Supposons que nous introduisons dans la banque le montant D 0 et nous payons un taux d'intérêt r. Nous appellerons D ( t ) à la quantité que nous aurons dans t ans. La variation de la quantité sera la somme de la variation par accumulation d'intérêts et la variation de revenus que nous effectuons à la banque, p de formule.
Il ya donc à modéliser dans la vie quotidienne en utilisant des équations différentielles.
Difficultés de résolution
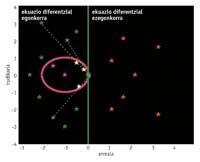
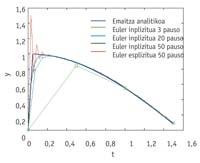
Une fois l'équation différentielle obtenue, il doit être résolu. Parfois, sa libération analytique n'est pas possible, et par des méthodes numériques on obtient un résultat approximatif. Les équations différentielles comprennent des autovaleurs complexes que nous appellerons l. Lorsque la partie réelle de ces auto-valeurs est positive, l'équation différentielle est instable et le résultat approximatif que nous obtiendrions en utilisant une méthode numérique pour sa libération n'a pas à ressembler à la solution réelle, car un petit changement a un fort impact sur eux. Par conséquent, les méthodes numériques sont appliquées à des équations différentielles stables, autobalioïdes de partie réelle négative. D'autre part, la méthode elle-même a également une zone de stabilité. Et si l'on veut obtenir un bon résultat, les autovaleurs doivent se situer là. Par conséquent, les autovaleurs des équations différentielles stables non présentes dans cette zone sont transférées à la zone de stabilité, en multipliant les autovaleurs par un nombre h mesuré (0,1) que nous appellerons mesure du passage.
La mesure de l'étape est essentielle pour résoudre l'équation et, bien sûr, ne peut pas être un nombre quelconque. En termes de fiabilité, la méthode de résolution doit être assez petite pour rester à l'intérieur de la zone de stabilité et assez grande pour prendre le moins de mesures possibles face au travail. Comment obtenir cet équilibre ?
Équilibre de la zone de stabilité
Pour savoir quelles étapes peuvent être faites dans la méthode numérique, il faut fixer l'erreur. Lorsque vous utilisez des méthodes numériques, une erreur locale est générée à chaque étape. Mais il ya une autre erreur qui apparaît dans la longueur, qui est la reproduction des erreurs de chaque étape, et qui est formé par les puissances d'un nombre appelé facteur d'amplification. Pour éviter l'augmentation de l'erreur, le facteur d'amplification doit être inférieur à l'unité. La zone qui remplit cette condition est connue comme zone de stabilité de la méthode. Or, l'autovaleur l doit être dans la zone de stabilité après s'être multipliée par h pour que le facteur d'amplification soit inférieur à l'unité. Mais non seulement cela, une fois que le produit l .h est dans la zone de stabilité, on voit si le nombre h doit être inférieur, puisque n'importe quel nombre qui est inférieur à h que nous avons trouvé, il est possible qu'après la multiplication de l'autovaleur soit porté à la zone. Parmi les nombres qui permettent de porter l'autovaleur au champ, le nombre h qui maintient l'erreur locale dans une tolérance est celui qui est choisi comme mesure de passage. Cette mesure de passage permet de contrôler les deux erreurs (local et longitudinal). Plus ce nombre est grand, plus le nombre d'étapes que nous pouvons faire et plus le résultat est rapide, un objectif que le grand champ de stabilité permet d'atteindre.

La méthode elle-même conditionne également la mesure de la zone de stabilité. Les méthodes implicites ont généralement une plus grande stabilité que les méthodes explicites, mais elles présentent également des inconvénients: la principale est qu'il faut des opérations plus ou moins complexes que dans les méthodes explicites. Par conséquent, lorsque les autovaleurs ne sont pas très grandes, la méthode explicite est préférée, car les opérations à effectuer seront plus durables.
Le rêve serait de trouver la stabilité maximale dans les ordres élevés et les méthodes explicites, mais dans ce domaine de la science il n'y a pas de rareté. Afin d'obtenir que les équations différentielles soient facilement relâchées par des méthodes numériques, de nombreux travaux sont effectués pour augmenter le champ de stabilité. Les premiers sont les méthodes d'Adams Bashforth et Moulton, qui utilisent à la fois les informations de la dernière étape et les informations d'autres étapes plus rapides pour construire la prochaine étape. De cette façon, on réussit à monter l'ordre de la méthode numérique, et celui de l'ordre 1 a un champ plus grand que celui d'Euler explicite (également d'ordre 1). L'une des propositions les plus importantes a été la BDF (formule backward differentiation) réalisée par Gear vers 1971, une méthode implicite qui utilisait des informations en plusieurs étapes plus légères. La méthode BDF a rendu les zones de stabilité aussi importantes dans des ordres élevés. Dernièrement, les méthodes utilisant la dérivée 2 ou les points dits superfuturs prédominent, car elles ont de grandes zones de stabilité, même si elles augmentent le travail à effectuer à chaque étape.

Beaucoup de petites étapes ou quelques grandes étapes, voici la clé. Dans cette compétition, la première option, avec de nombreuses petites étapes, a l'avantage de la fiabilité et la deuxième l'optimisation du travail. Unifier les deux options en une seule fois serait excellent, car il obtiendrait "fiabilité sans travail excessif". La clé pour briser cet équilibre réside dans des méthodes de grand champ de stabilité, qui ne mettent pas de limites aussi rigides à la mesure du passage. C'est pourquoi il est possible de prendre des mesures non fiables et de grandes étapes fiables.