Histoire des chiffres (I)
Préhistoire
Les êtres humains d'autrefois se servaient des sens pour exprimer des quantités qui, comme certains animaux, n'étaient pas capables de distinguer de grandes quantités (comme aujourd'hui nous ne comprenons pas la quantité de trois trillions).
Les premiers numéros qui ont été inventés ont été un et deux. Une pour s'exprimer (dans un groupe). Aussi pour exprimer au pénis (pour se différencier des femmes) ou à l'homme (pour se différencier des animaux).
Bia était l'expression de la duplicité (autonomisation et virilité, vie et mort, vérité et fausse, bien et mal, etc.). ).
En général, on peut dire qu'à partir de là (deux) pour séparer de plus grandes quantités n'étaient pas utilisés symboles spéciaux et quand ils devaient représenter de grandes quantités, le même symbole était utilisé, indépendamment du montant. Ses témoins peuvent être trouvés dans plusieurs langues de son entourage : en français, trois (trois) et très (très), en anglais three (trois) et throng (une machine), en latin, seuls les quatre premiers numéros étaient déclinés.
On pourrait donc dire qu’à cette époque «la capacité humaine quant à la compréhension des nombres ne passait pas par quatre». Cela ne devrait pas nous surprendre si nous considérons que, à première vue, nous ne sommes pas en mesure de deviner combien de voitures il ya dans une rangée.
Comment les premiers habitants ont-ils appris à compter ? Pour répondre à cette question, il faut distinguer et comprendre les deux formes des nombres: cardinal et ordinal. Voici un exemple : Si nous disons « 28 jours de février », nous parlons du nombre de jours de février. Par conséquent, le numéro 28 indique un cardinal. Au contraire, si nous disons « aujourd’hui c’est le 28 février », nous disons aujourd’hui que c’est le 28 février. Nous indiquons donc l'ordre, c'est-à-dire la forme ordinale.
Au début ils ont employé la méthode d'appariement, c.-à-d., dans un bâton faisant une sangria pour chaque grain, ou attrapaient une pierre, ou jouaient une partie du corps. Mais ce n'était pas une grande avancée. Et quand ils devaient recompter la même chose, ils devaient refaire des saignements. Par exemple, quand un troupeau de moutons sortait le matin et le gardaient le soir, ils devaient compter pour savoir si quelque chose avait été perdu.
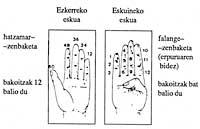
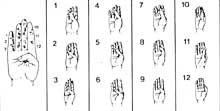
Les papous de Nouvelle-Guinée utilisaient le corps pour quantifier au début de ce siècle. Chaque partie du corps indiquait un nombre et pour le comptabiliser jusqu'à un nombre, en gardant l'ordre dans lequel les parties correspondant à tous les numéros précédents étaient jouées. Par exemple, pour compter 10 jouaient le copeau (1) de la main droite, le locataire (2), le milieu (3), l'index (4) et le pouce (5), puis le poignet (6), le coude (7), l'épaule (8), l'oreille (9) et l'œil (10). Mais si une fois fait cela signifiait qu'ils avaient compté 10, ils ne touchaient pas directement l'œil droit, mais commençaient par le copeau (1). Cela nous dit qu'ils n'avaient aucune idée abstraite des nombres.
Ce qui est exposé ici est applicable aux anciens voisins et sans lèvres nous pouvons dire que le corps a été le premier support de l'arithmétique. C'est la coutume de compter sur les doigts des mains qui vivent encore.
Nous pourrions dire que ces techniques ont également appris à compter tout en apprenant à différencier les deux formes. Il a été démontré que la capacité de différenciation était humaine. Nous utilisons les deux formes si souvent que nous oublions souvent la différence.
Invention de bases
Une fois la capacité de séparation atteinte, ils rencontrèrent un autre problème : pierres, bâtons, entailles, etc., qui ne pouvaient comptabiliser de grandes quantités. utilisation continue. La solution n'était pas, d'autre part, donner un nom spécial à chaque nombre (nombre). Par conséquent, l'être humain a été trouvé dans la nécessité d'exprimer au moins les plus grandes quantités de symboles.
Pour y parvenir, différents peuples ont inventé différents systèmes. Le plus répandu est celui de base 10. Beaucoup de peuples l'ont utilisé, mais comment ont-ils fait? Pour répondre, prenons un exemple (pensez qu'ils ne savaient pas encore écrire): ils prenaient des bandes de différentes couleurs; blanc, bleu, rouge,… Sur la bande blanche de chaque animal ils mettaient une coquille. Sur cette bande, quand il y avait dix coquillages, on les tirait et on mettait une dans la bande bleue. Les coquillages étaient repris sur la bande blanche. Puis, quand dans la bande bleue ils accumulaient dix coquillages, ils les sortaient et mettaient une dans la bande rouge. Ainsi, quand les animaux finissaient, ils avaient deux coquillages en bande rouge, six bandes bleues et trois bandes blanches, indiquant le nombre de 263. Tout cela ne faisait pas confiance.
La preuve de l'utilisation de ce système peut être trouvée dans plusieurs langues, comme le système de numérotation orale chinois:
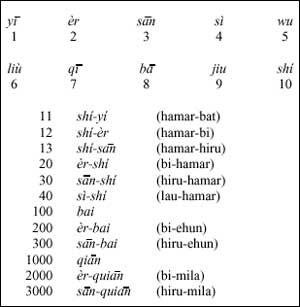
La base 10 a un avantage sur de plus grandes bases, son utilité. Mais pourquoi ne pas avoir de bases plus petites? Nous devrions chercher dans les déclarations la raison: 4326 sur deux bases 11100110 Comme vous le savez, plus de chiffres sont nécessaires.
Mais l'utilisation de la base dix ne doit pas être recherchée dans les avantages mathématiques, mais dans nos mains. Et c'est que l'homme a toujours utilisé les mains pour compter, et dans les mains il ya dix doigts.
La base dix n'est pas la seule qui a été utilisée. Les bases cinq, vingt, douze et soixante ont également été utilisées.
La raison pour laquelle nous utilisons la base 5 se trouve dans la main. Pour le comptage on utilisait les doigts d'une main et les objets se groupaient en cinq, c'est-à-dire quand dans la main gauche il y avait cinq doigts levés descendaient et dans la main droite on levait un. Ainsi ils pouvaient compter jusqu'à vingt. L'empreinte de cinq bases peut être trouvée en plusieurs langues. Par exemple, dans la langue Api des Nouvelles Hébrides

Nous pouvons également trouver des exemples de vingt bases sans aller plus loin, en basque. Les vingt premiers numéros en basque ont un nom et sont ensuite regroupés en vingt :

Autres exemples: Maia, ...
Les peuples qui utilisaient cette base ont également pris en compte les orteils au moment de compter.
La base douze est plus large que la précédente et a un grand avantage sur dix: Le nombre 12 a des diviseurs 2, 3, 4 et 6, facilitant le calcul pour la division. Nous avons la “douzaine” et la “épaisse” (12 douzaines) qui vivent encore sur cette base. Parmi les peuples qui ont utilisé cette base se trouvent le Sumérien, le Babylonien et le Romain.
Son origine est inconnue, mais nous devrions probablement le chercher à la main. Et c'est que, en éliminant le pouce, sur les quatre autres doigts il y a trois phalange, formant un total de douze phalange. Cette base est actuellement utilisée en Inde, Pakistan, Afghanistan, Egypto, Syrie, Turquie, etc.
Sans doute, la base la plus énigmatique est la sexagésimale. Comme unité de compter devient lourd. Cependant, de nombreux peuples l'ont utilisé tout au long de l'histoire. Nous avons ses traces. Par exemple, la mesure du temps se fait en heures, minutes et secondes ; les arcs et angles s'expriment en soixante bases par degrés, minutes et secondes.
Les Sumériens ont été les premiers à l'utiliser. Ils ont passé les mathématiciens et les astronomes babyloniens et ceux-ci aux Grecs et les Arabes.
Il existe différentes hypothèses sur l'origine de cette base. L'un d'eux fonde son argument sur l'union de deux civilisations différentes. Pensons que si l'on utilisait la base dix et l'autre la base douze, si l'on recueillait les deux, selon cette hypothèse, ils pouvaient atteindre la base soixante. En fait, le plus petit multiple des nombres 10 et 12 est le 60.
Une autre possibilité, dans la même hypothèse, serait composée de cinq et douze bases. L'avantage de ce cas est le produit des numéros 60, 5 et 12. Par conséquent, il ne faudrait pas chercher le plus petit multiple des communs. En outre, dans le langage sumérien, on peut trouver des indices de l’apparition de cinq bases:

Premières calculatrices
L'homme, comme il avançait dans l'utilisation du concept de nombre, cherchait à résoudre des problèmes plus profonds. Dans le même temps, les ressources ont été améliorées. Nous pouvons dire que la fonction la plus importante de l'être humain d'alors a été de faciliter la comptabilité patrimoniale.
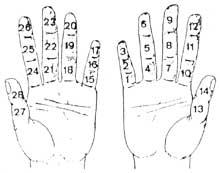
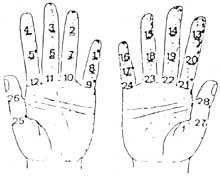
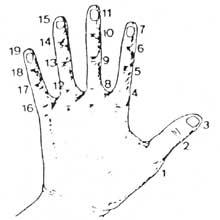
Au début, ils avaient les mains. Par conséquent, nous pouvons considérer que la première calculatrice était la main. Même si cela ne semble pas, on peut compter dix milliards de mains. Différentes méthodes ont été développées en utilisant des phalanges et des articulations entre phalanges. Pour leur comptabilisation, ils mettaient des lacets ou d'autres signaux sur les doigts ou le nombre qu'ils jouaient avec l'autre main. Mais l'utilisation de la main n'a pas été limitée à compter. Ils effectuaient aussi des calculs manuels. Par exemple, ils savaient multiplier manuellement.
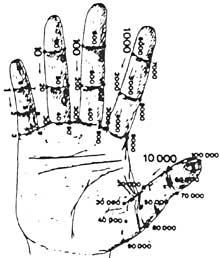
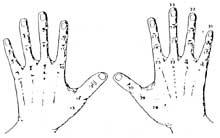

Cependant, les mains indiquaient seulement les chiffres, mais ils ne pouvaient pas les garder en mémoire. Lorsque les relations entre les sociétés se sont accentuées avec le développement du commerce, l'homme a rencontré un autre problème: comment mémoriser ce que j'avais compté jusqu'alors?
Il a été doté de différentes méthodes et outils pour résoudre ce problème. À titre d’exemple, nous mentionnerons le « quipu » (nœud) utilisé par les appâts. Il avait une corde principale à laquelle se joignaient d'autres groupes de corde, placés sur des tronçons réguliers. Bien que ces outils remplissent de nombreuses autres fonctions, ils étaient principalement utilisés pour comptabiliser. Des entraves de nombres (quantités) étaient faites dans les cordes. Actuellement, cette méthode peut être trouvée dans: Sibérie, Hawaï, Nigeria, Nouveau-Mexique, etc.

Une autre méthode préhistorique était celle des os ou du bois. L'empreinte la plus ancienne de l'ère “Aurignac” (a. C. Il nous arrive entre 35.000 et 20.000).
Au début, la méthode consistait à faire des saignements. Plus tard, différents systèmes ont été améliorés et utilisés. Chaque type d'objet était marqué avec un symbole spécial sur le bâton ou l'os. Il y a 150 ans, les archives étaient transférées à la Ministre des finances de Grande-Bretagne. XIX. Au début du XXe siècle, les livres de comptes dans l'État français, la Suisse, l'Allemagne, etc. étaient des bâtons (tayas). Cette méthode a été utilisée comme reçu, facture ou carte de crédit dans les échanges entre le commerce et le client.
Il existe, cependant, une autre méthode qui a le plus influencé l'arithmétique et la comptabilité, est celle de l'accumulation de pierres (pierres, cannes, coquillages, noix, etc. ).
L'accumulation de pierres, avec la méthode de la sangria, indique le degré 0 de comptage, car il n'a pas besoin d'une découverte abstraite des nombres.
Quand l'homme a commencé à utiliser les bases, il s'est avéré assez flexible pour avancer.
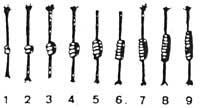


Actuellement, la méthode de congestion est utilisée dans certains tributs comme signe de différenciation et de richesse. Cette méthode a aidé l'homme à se former dans le calcul. Le mot calcul vient du mot latin “calculus”, dont la signification est “pierre arrondie”. La même étymologie peut être trouvée dans d’autres langues: en grec le mot “pséphos” a des significations “nombres” et “une pierre”; en arabe les mots “haswa” (récif) et “ihsa” (numérotation, statistique) ont la même racine. Les quilles sont à l'origine des marqueurs d'abaque et de boules.
Les premières abaques étaient faites sur le sol par des tranchées parallèles. Ensuite, sur des panneaux ou des pierres, par des lignes parallèles. Chaque tranchée et ligne avait une valeur différente, la valeur étant soumise à la base. Les pierres, les calculus, et plus tard les tuiles, étaient placées sur des tranchées et des raies, chacune prenant la valeur de la ligne ou tranchée.
Sur le côté Est, au contraire, des marqueurs à billes ont été créés avec le même fonctionnement. En plus de ces instruments, ils pouvaient également effectuer des opérations. Aujourd'hui, il y a encore une grande habitude d'utiliser les abaques en Chine, au Japon, en URSS et à l'est.