Història de les xifres (I)
Prehistòria
Els éssers humans d'antany se servien dels sentits per a expressar quantitats que, com alguns animals, no eren capaços de distingir grans quantitats (com avui no entenem la quantitat de tres trilions).
Els primers números que es van inventar van ser un i dos. Una per a expressar-se (dins d'un grup). També per a expressar al penis (per a diferenciar-se de les dones) o a l'home (per a diferenciar-se dels animals).
Bia era expressió de la duplicitat (apoderament i virilitat, vida i mort, veritat i falsa, bé i malament, etc.).
En general, es pot dir que a partir d'aquí (dos) per a separar majors quantitats no s'utilitzaven símbols especials i quan havien de representar grans quantitats s'utilitzava el mateix símbol, independentment de la quantitat. Els seus testimonis es poden trobar en diverses llengües del seu entorn: en el francès són similars trois (tres) i très (molt), en l'anglès three (tres) i throng (una màquina), en el llatí només es declinaven els quatre primers números.
Es podria dir, per tant, que en aquella època “la capacitat humana quant a la comprensió dels números no passava per quatre”. Això no ha de sorprendre'ns si tenim en compte que, a primera vista, no som capaces d'endevinar quants cotxes hi ha en una fila.
Com van aprendre a comptar els primers habitants? Per a respondre a aquesta pregunta és necessari distingir i comprendre les dues formes dels números: cardinal i ordinal. A continuació es mostra un exemple: Si diem “Té 28 dies de febrer” parlem del nombre de dies de febrer. Per tant, el número 28 indica un cardinal. Per contra, si diem “avui és 28 de febrer”, avui estem dient que és el dia 28 de febrer. Per tant, indiquem l'ordre, és a dir, la forma ordinal.
Al principi van utilitzar el mètode d'aparellament, és a dir, en un pal que feia una sagnia per cada gra, o agafaven una pedra, o tocaven una part del cos. Però això no va ser un gran avanç. I és que quan havien de tornar a comptar el mateix havien de tornar a fer sagnies. Per exemple, quan un ramat d'ovelles sortia al matí i el guardaven a la tarda, havien de comptar per a saber si s'havia perdut alguna.
Els papúes de Nova Guinea utilitzaven el cos per a quantificar a principis d'aquest segle. Cada part del cos indicava un número i per a comptabilitzar-lo fins a un número, mantenint l'ordre en el qual es tocaven les parts corresponents a tots els números anteriors. Per exemple, per a comptar 10 tocaven l'encenall (1) de la mà dreta, l'inquilí (2), el mitjà (3), l'índex (4) i el polze (5), després la nina (6), el colze (7), l'espatlla (8), l'orella (9) i l'ull (10). Però si una vegada fet això significaven que havien comptat 10, no tocaven directament l'ull dret, sinó que començaven per l'encenall (1). Això ens diu que no tenien idea abstracta de números.
L'aquí exposat és aplicable als antics veïns i sense llavis podem dir que el cos va ser el primer suport de l'aritmètica. És el costum de comptar amb els dits de les mans que encara perviuen.
Podríem dir que amb aquestes tècniques també van aprendre a comptar al mateix temps que van aprendre a diferenciar totes dues formes. Va quedar demostrat que la capacitat de diferenciació era humana. Nosaltres utilitzem totes dues formes tan sovint que moltes vegades oblidem la diferència.
Invenció de bases
Una vegada aconseguida la capacitat de separació, es van trobar amb un altre problema: pedres, bastons, osques, etc., que no podien comptabilitzar grans quantitats. ús continu. La solució no era, d'altra banda, donar un nom especial a cada número (número). Per tant, l'ésser humà es va trobar en la necessitat d'expressar les majors quantitats de símbols com a mínim.
Per a aconseguir-ho, diferents pobles han inventat diferents sistemes. El més estès és el de base 10. Molts pobles ho han utilitzat, però com ho van fer?. Per a donar resposta, posarem un exemple (pensa que encara no sabien escriure): prenien tires de diferents colors; blanc, blau, vermell,… En la tira blanca de cada animal ficaven una petxina. En aquesta tira quan hi havia deu petxines les treien i ficaven una en la tira blava. En la tira blanca es reprenien les petxines. Després, quan en la tira blava acumulaven deu petxines, les treien i ficaven una en la tira vermella. Així, quan els animals acabaven tenien dues petxines en tira vermella, sis tires blaves i tres tires blanques, indicant el número de 263. Tot això ho feien sense fiar.
La prova de l'ús d'aquest sistema la podem trobar en diversos idiomes, com el sistema de numeració oral xinès:
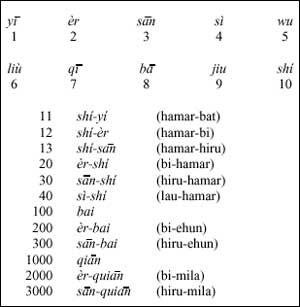
La base 10 té un avantatge sobre bases més grans, la seva utilitat. Però, per què no tenir bases més petites?. Hauríem de buscar en les declaracions el motiu: 4326 en dues bases 11100110 Com saps, es necessiten més xifres.
Però l'ús de la base deu no ha de buscar-se en els avantatges matemàtics, sinó a les nostres mans. I és que l'home sempre ha utilitzat les mans per a comptar, i a les mans hi ha deu dits.
La base deu no és l'única que s'ha utilitzat. També s'han utilitzat les bases cinc, vint, dotze i seixanta.
El motiu pel qual utilitzem la base 5 el trobem a la mà. Per al comptatge s'utilitzaven els dits d'una mà i els objectes s'agrupaven en cinc, és a dir, quan a la mà esquerra hi havia cinc dits aixecats es baixaven i a la mà dreta s'aixecava un. Així podien comptar fins a vint. La petjada de cinc bases pot trobar-se en diversos idiomes. Per exemple, en la llengua Api de les Noves Hebridas

També podem trobar exemples de vint bases sense anar més lluny, en euskara. Els vint primers números en basc tenen nom i a partir d'aquí s'agrupen en vint:

Altres exemples: Maia, ...
Els pobles que utilitzaven aquesta base també tenien en compte els dits del peu a l'hora de comptar.
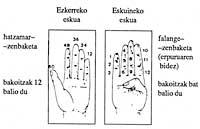
La base dotze és més àmplia que l'anterior i té un gran avantatge sobre deu: El número 12 té divisors 2, 3, 4 i 6, facilitant el càlcul per a la divisió. Tenim la “dotzena” i la “gruixuda” (12 dotzenes) que encara perviuen en aquesta base. Entre els pobles que van utilitzar aquesta base destaquen el sumeriano, el babilònic i el romà.
El seu origen és desconegut, però probablement hauríem de buscar-lo a la mà. I és que, eliminant el polze, en els altres quatre dits hi ha tres falange, formant un total de dotze falange. Aquesta base s'utilitza actualment a l'Índia, el Pakistan, Afghanistán, Egypto, Syria, Turquia, etc.
Sens dubte, la base més enigmàtica és la sexagesimal. Com a unitat de comptar es fa pesat. No obstant això, són molts els pobles que ho han utilitzat al llarg de la història. Tenim les seves petjades. Per exemple, el mesurament del temps es realitza en hores, minuts i segons; els arcs i angles s'expressen en seixanta bases mitjançant graus, minuts i segons.
Els sumerianos van ser els primers a usar-ho. Aquests van passar als matemàtics i astrònoms babilonis i aquests als grecs i àrabs.
Existeixen diferents hipòtesis sobre l'origen d'aquesta base. Un d'ells basa el seu argument en la unió de dues civilitzacions diferents. Pensem que si un utilitzava la base deu i l'altre la base dotze, si recollia ambdues, segons aquesta hipòtesi, podien aconseguir la base seixanta. De fet, el múltiple més petit dels números 10 i 12 és el 60.
Una altra possibilitat, en la mateixa hipòtesi, estaria composta per cinc i dotze bases. L'avantatge d'aquest cas és el producte dels números 60, 5 i 12. Per tant, no caldria buscar el múltiple més petit dels comuns. A més, en el llenguatge sumeriano es poden trobar indicis de l'aparició de cinc bases:

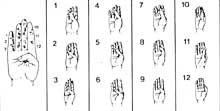
Primeres calculadores
L'home, a mesura que avançava en la utilització del concepte de número, tractava de resoldre problemes més profunds. Al mateix temps, els recursos van anar millorant. Podem dir que la funció més important de l'ésser humà de llavors va ser la de facilitar la comptabilitat patrimonial.
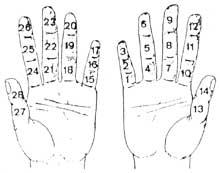
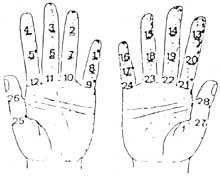
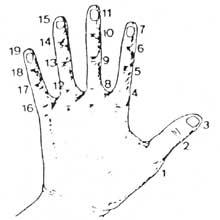
Al principi comptaven amb les mans. Per tant, podem considerar que la primera calculadora va ser la mà. Encara que no ho sembli, amb les mans es poden comptar deu mil milions. Es van desenvolupar diferents mètodes utilitzant falanges i articulacions entre falanges. Per a la seva comptabilització, posaven cordons o altres senyals en els dits o el número que tocava amb l'altra mà. Però l'ús de la mà no es va limitar a comptar. També realitzaven càlculs manuals. Per exemple, sabien multiplicar manualment.
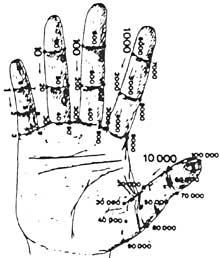
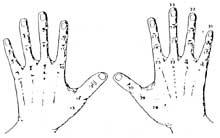

No obstant això, amb les mans només indicaven els números, però no podien guardar-los en la memòria. Quan les relacions entre les societats es van accentuar amb el desenvolupament del comerç, l'home es va trobar davant un altre problema: com memoritzar el que havia comptat fins llavors?
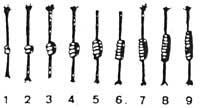
Es va dotar de diferents mètodes i eines per a abordar aquest problema. A tall d'exemple, esmentarem el “quipu” (nus) que usaven els cechueros. Tenia una corda principal a la qual s'unien altres grups de corda, col·locats en trams regulars. Encara que aquestes eines complien moltes altres funcions, s'utilitzaven principalment per a comptabilitzar. En les cordes es feien traves de números (quantitats). Actualment aquest mètode es pot trobar en: Sibèria, Hawaii, Nigèria, Nou Mèxic, etc.

Un altre mètode prehistòric era el dels ossos o la fusta. La petjada més antiga de l'era “Aurignac” (a. C. Ens arriba entre 35.000 i 20.000).
Al principi el mètode consistia a fer sagnies. Posteriorment es va anar millorant i es van utilitzar diferents sistemes. Cada tipus d'objecte s'assenyalava amb un símbol especial en el pal o os. Fa 150 anys s'emportaven els arxius en la Ministra d'Hisenda del Gran Bretanya. XIX. A principis del segle XX els llibres de comptes en l'Estat francès, Suïssa, Alemanya, etc. eren pals (tayas). Aquest mètode s'ha utilitzat com a rebut, factura o targeta de crèdit en els intercanvis entre el comerç i el client.
Existeix, no obstant això, un altre mètode que ha influït més en l'aritmètica i comptabilitat, és el de l'acumulació de pedres (pedres, o bastons, petxines, fruita seca, etc.).
L'acumulació de pedres, juntament amb el mètode de la sagnia, indica el grau 0 de comptatge, ja que no necessita d'un descobriment abstracte dels números.
Quan l'home va començar a utilitzar les bases, va resultar bastant flexible per a avançar.


En l'actualitat s'utilitza el mètode de la congestió en alguns tributs com a signe de diferenciació i riquesa. Aquest mètode ha ajudat l'home a formar-se en el càlcul. La paraula càlcul prové de la paraula llatina “calculus”, el significat de la qual és “pedra arrodonida”. La mateixa etimologia es pot trobar en altres llengües: en grec la paraula “pséphos” té significats “números” i “una pedra”; en àrab les paraules “haswa” (escull) i “ihsa” (numeració, estadística) tenen la mateixa arrel. Les bitlles són l'origen dels marcadors d'àbac i boles.
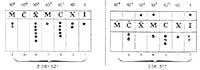
Els primers àbacs es feien en el sòl mitjançant rases paral·leles. Posteriorment en taulers o pedres, mitjançant línies paral·leles. Cada rasa i línia tenia un valor diferent, estant el valor subjecte a la base. Les pedres, els calculus, i més tard les fitxes, es col·locaven sobre rases i ratlles, cadascuna d'elles prenia el valor de la línia o rasa.
En el costat Aquest, per contra, es van crear marcadors de boles amb el mateix funcionament. A més de comptar amb aquests instruments, també podien realitzar operacions. En l'actualitat encara existeix un gran costum d'utilitzar els àbacs a la Xina, el Japó, URSS i tot l'est.