Historia de las cifras (I)
Prehistoria
Los seres humanos de antaño se servían de los sentidos para expresar cantidades que, como algunos animales, no eran capaces de distinguir grandes cantidades (como hoy no entendemos la cantidad de tres trillones).
Los primeros números que se inventaron fueron uno y dos. Una para expresarse (dentro de un grupo). También para expresar al pene (para diferenciarse de las mujeres) o al hombre (para diferenciarse de los animales).
Bia era expresión de la duplicidad (empoderamiento y virilidad, vida y muerte, verdad y falsa, bien y mal, etc.).
En general, se puede decir que a partir de ahí (dos) para separar mayores cantidades no se utilizaban símbolos especiales y cuando tenían que representar grandes cantidades se utilizaba el mismo símbolo, independientemente de la cantidad. Sus testigos se pueden encontrar en varias lenguas de su entorno: en el francés son similares trois (tres) y très (muy), en el inglés three (tres) y throng (una máquina), en el latín sólo se declinaban los cuatro primeros números.
Se podría decir, por tanto, que en aquella época “la capacidad humana en cuanto a la comprensión de los números no pasaba por cuatro”. Esto no debe sorprendernos si tenemos en cuenta que, a primera vista, no somos capaces de adivinar cuántos coches hay en una fila.
¿Cómo aprendieron a contar los primeros habitantes? Para responder a esta pregunta es necesario distinguir y comprender las dos formas de los números: cardinal y ordinal. A continuación se muestra un ejemplo: Si decimos “Tiene 28 días de febrero” hablamos del número de días de febrero. Por lo tanto, el número 28 indica un cardinal. Por el contrario, si decimos “hoy es 28 de febrero”, hoy estamos diciendo que es el día 28 de febrero. Por tanto, indicamos el orden, es decir, la forma ordinal.
En un principio utilizaron el método de emparejamiento, es decir, en un palo que hacía una sangría por cada grano, o cogían una piedra, o tocaban una parte del cuerpo. Pero eso no fue un gran avance. Y es que cuando tenían que volver a contar lo mismo tenían que volver a hacer sangrías. Por ejemplo, cuando un rebaño de ovejas salía por la mañana y lo guardaban por la tarde, tenían que contar para saber si se había perdido alguna.
Los papúes de Nueva Guinea utilizaban el cuerpo para cuantificar a principios de este siglo. Cada parte del cuerpo indicaba un número y para contabilizarlo hasta un número, manteniendo el orden en el que se tocaban las partes correspondientes a todos los números anteriores. Por ejemplo, para contar 10 tocaban la viruta (1) de la mano derecha, el inquilino (2), el medio (3), el índice (4) y el pulgar (5), luego la muñeca (6), el codo (7), el hombro (8), la oreja (9) y el ojo (10). Pero si una vez hecho esto significaban que habían contado 10, no tocaban directamente el ojo derecho, sino que comenzaban por la viruta (1). Esto nos dice que no tenían idea abstracta de números.
Lo aquí expuesto es aplicable a los antiguos vecinos y sin labios podemos decir que el cuerpo fue el primer soporte de la aritmética. Es la costumbre de contar con los dedos de las manos que aún perviven.
Podríamos decir que con estas técnicas también aprendieron a contar al mismo tiempo que aprendieron a diferenciar ambas formas. Quedó demostrado que la capacidad de diferenciación era humana. Nosotros utilizamos ambas formas tan a menudo que muchas veces olvidamos la diferencia.
Invención de bases
Una vez conseguida la capacidad de separación, se encontraron con otro problema: piedras, bastones, muescas, etc., que no podían contabilizar grandes cantidades. uso continuo. La solución no era, por otra parte, dar un nombre especial a cada número (número). Por lo tanto, el ser humano se encontró en la necesidad de expresar las mayores cantidades de símbolos como mínimo.
Para conseguirlo, diferentes pueblos han inventado diferentes sistemas. El más extendido es el de base 10. Muchos pueblos lo han utilizado, pero ¿cómo lo hicieron?. Para dar respuesta, vamos a poner un ejemplo (piensa que todavía no sabían escribir): tomaban tiras de diferentes colores; blanco, azul, rojo,… En la tira blanca de cada animal metían una concha. En esta tira cuando había diez conchas las sacaban y metían una en la tira azul. En la tira blanca se retomaban las conchas. Luego, cuando en la tira azul acumulaban diez conchas, las sacaban y metían una en la tira roja. Así, cuando los animales terminaban tenían dos conchas en tira roja, seis tiras azules y tres tiras blancas, indicando el número de 263. Todo esto lo hacían sin fiar.
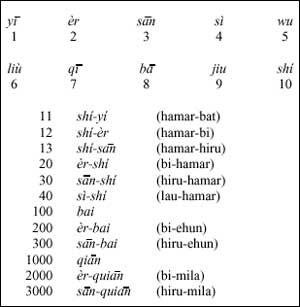
La prueba del uso de este sistema la podemos encontrar en varios idiomas, como el sistema de numeración oral chino:
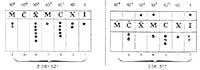
La base 10 tiene una ventaja sobre bases más grandes, su utilidad. Pero, ¿por qué no tener bases más pequeñas?. Deberíamos buscar en las declaraciones el motivo: 4326 en dos bases 11100110 Como sabes, se necesitan más cifras.
Pero el uso de la base diez no debe buscarse en las ventajas matemáticas, sino en nuestras manos. Y es que el hombre siempre ha utilizado las manos para contar, y en las manos hay diez dedos.
La base diez no es la única que se ha utilizado. También se han utilizado las bases cinco, veinte, doce y sesenta.
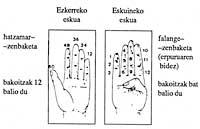
El motivo por el que utilizamos la base 5 lo encontramos en la mano. Para el conteo se utilizaban los dedos de una mano y los objetos se agrupaban en cinco, es decir, cuando en la mano izquierda había cinco dedos levantados se bajaban y en la mano derecha se levantaba uno. Así podían contar hasta veinte. La huella de cinco bases puede encontrarse en varios idiomas. Por ejemplo, en la lengua Api de las Nuevas Hebridas

También podemos encontrar ejemplos de veinte bases sin ir más lejos, en euskara. Los veinte primeros números en euskera tienen nombre y a partir de ahí se agrupan en veinte:

Otros ejemplos: Maia, ...
Los pueblos que utilizaban esta base también tenían en cuenta los dedos del pie a la hora de contar.
La base doce es más amplia que la anterior y tiene una gran ventaja sobre diez: El número 12 tiene divisores 2, 3, 4 y 6, facilitando el cálculo para la división. Tenemos la “docena” y la “gruesa” (12 docenas) que todavía perviven en esta base. Entre los pueblos que utilizaron esta base destacan el sumeriano, el babilónico y el romano.
Su origen es desconocido, pero probablemente deberíamos buscarlo en la mano. Y es que, eliminando el pulgar, en los otros cuatro dedos hay tres falange, formando un total de doce falange. Esta base se utiliza actualmente en India, Pakistán, Afghanistán, Egypto, Syria, Turquía, etc.
Sin duda, la base más enigmática es la sexagesimal. Como unidad de contar se hace pesado. Sin embargo, son muchos los pueblos que lo han utilizado a lo largo de la historia. Tenemos sus huellas. Por ejemplo, la medición del tiempo se realiza en horas, minutos y segundos; los arcos y ángulos se expresan en sesenta bases mediante grados, minutos y segundos.
Los sumerianos fueron los primeros en usarlo. Estos pasaron a los matemáticos y astrónomos babilonios y éstos a los griegos y árabes.
Existen diferentes hipótesis sobre el origen de esta base. Uno de ellos basa su argumento en la unión de dos civilizaciones diferentes. Pensemos que si uno utilizaba la base diez y el otro la base doce, si recogía ambas, según esta hipótesis, podían alcanzar la base sesenta. De hecho, el múltiplo más pequeño de los números 10 y 12 es el 60.
Otra posibilidad, en la misma hipótesis, estaría compuesta por cinco y doce bases. La ventaja de este caso es el producto de los números 60, 5 y 12. Por lo tanto, no habría que buscar el múltiplo más pequeño de los comunes. Además, en el lenguaje sumeriano se pueden encontrar indicios de la aparición de cinco bases:

Primeras calculadoras
El hombre, a medida que avanzaba en la utilización del concepto de número, trataba de resolver problemas más profundos. Al mismo tiempo, los recursos fueron mejorando. Podemos decir que la función más importante del ser humano de entonces fue la de facilitar la contabilidad patrimonial.
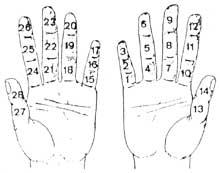
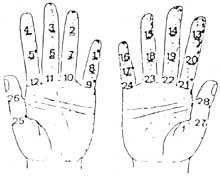
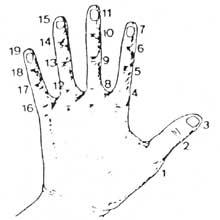
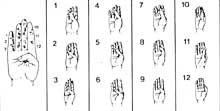
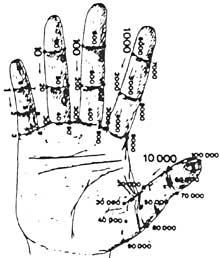
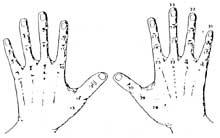
En un principio contaban con las manos. Por lo tanto, podemos considerar que la primera calculadora fue la mano. Aunque no lo parezca, con las manos se pueden contar diez mil millones. Se desarrollaron diferentes métodos utilizando falanges y articulaciones entre falanges. Para su contabilización, ponían cordones u otras señales en los dedos o el número que tocaba con la otra mano. Pero el uso de la mano no se limitó a contar. También realizaban cálculos manuales. Por ejemplo, sabían multiplicar manualmente.

Sin embargo, con las manos sólo indicaban los números, pero no podían guardarlos en la memoria. Cuando las relaciones entre las sociedades se acentuaron con el desarrollo del comercio, el hombre se encontró ante otro problema: ¿cómo memorizar lo que había contado hasta entonces?
Se dotó de diferentes métodos y herramientas para abordar este problema. A modo de ejemplo, mencionaremos el “quipu” (nudo) que usaban los cechueros. Tenía una cuerda principal a la que se unían otros grupos de cuerda, colocados en tramos regulares. Aunque estas herramientas cumplían muchas otras funciones, se utilizaban principalmente para contabilizar. En las cuerdas se hacían trabas de números (cantidades). Actualmente este método se puede encontrar en: Siberia, Hawai, Nigeria, Nuevo México, etc.

Otro método prehistórico era el de los huesos o la madera. La huella más antigua de la era “Aurignac” (a. C. Nos llega entre 35.000 y 20.000).
Al principio el método consistía en hacer sangrías. Posteriormente se fue mejorando y se utilizaron diferentes sistemas. Cada tipo de objeto se señalaba con un símbolo especial en el palo o hueso. Hace 150 años se llevaban los archivos en la Ministra de Hacienda del Gran Bretaña. XIX. A principios del siglo XX los libros de cuentas en el Estado francés, Suiza, Alemania, etc. eran palos (tayas). Este método se ha utilizado como recibo, factura o tarjeta de crédito en los intercambios entre el comercio y el cliente.
Existe, sin embargo, otro método que ha influido más en la aritmética y contabilidad, es el de la acumulación de piedras (piedras, o bastones, conchas, frutos secos, etc.).
La acumulación de piedras, junto con el método de la sangría, indica el grado 0 de conteo, ya que no necesita de un descubrimiento abstracto de los números.
Cuando el hombre empezó a utilizar las bases, resultó bastante flexible para avanzar.
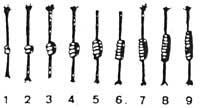


En la actualidad se utiliza el método de la congestión en algunos tributos como signo de diferenciación y riqueza. Este método ha ayudado al hombre a formarse en el cálculo. La palabra cálculo proviene de la palabra latina “calculus”, cuyo significado es “piedra redondeada”. La misma etimología se puede encontrar en otras lenguas: en griego la palabra “pséphos” tiene significados “números” y “una piedra”; en árabe las palabras “haswa” (arrecife) y “ihsa” (numeración, estadística) tienen la misma raíz. Los bolos son el origen de los marcadores de ábaco y bolas.
Los primeros ábacos se hacían en el suelo mediante zanjas paralelas. Posteriormente en tableros o piedras, mediante líneas paralelas. Cada zanja y línea tenía un valor diferente, estando el valor sujeto a la base. Las piedras, los calculus, y más tarde las fichas, se colocaban sobre zanjas y rayas, cada una de ellas tomaba el valor de la línea o zanja.
En el lado Este, por el contrario, se crearon marcadores de bolas con el mismo funcionamiento. Además de contar con estos instrumentos, también podían realizar operaciones. En la actualidad todavía existe una gran costumbre de utilizar los ábacos en China, Japón, URSS y todo el este.