Números
Estes conxuntos represéntanse coas letras N, Z, Q, R, C respectivamente, e cumpren que cada un deles pertenza ao grupo seguinte. Isto adoita dicirse matematicamente N\ Z Q Q B C.
Pero todo isto é una mera teoría, xa que na realidade, na rúa, os números máis utilizados son os do grupo Z e como moito os do grupo Q. De feito, os números tipo 1, 2, 1000, 3627 son os que máis se utilizan e, por dicilo dalgunha maneira, si queremos expresar as débedas, pomos diante os números (–) en negativo. Por suposto, tamén se utilizan números decimais. Exemplo 2,13 m, 7,14 kg. 1,8 l, etc. Con todo, carpinteiros, fontaneiros, etc. substitúen o metro e o centímetro por milímetro como unidade á hora de indicar as medidas. Así, os números decimais convértense en simples: 2130 mm por exemplo.
Este uso dos números naturais, ademais de dar nome aos números, levou a moitos matemáticos a realizar unha profunda análise dos mesmos e a tantas persoas que non son matemáticas. O froito desta profundización é a teoría numérica. Esta teoría co matemático Fermat XVII. Podemos dicir que naceu no século XIX. Nese século, precisamente, publicouse o primeiro tratado sobre Xogos Matemáticos escrito polo poeta e cineasta Claude-Gaspard Bachet e Méziriac: Problemas plaisant detectables qui se font par noméeslles. Nela, ademais do xogo de naipes e números coñecidos naquela época, incluíanse cuestións máis profundas. Entre outros, a construción de cadrados máxicos e os problemas de análises ilimitadas.
Doutra banda, debemos considerar como froito tanto os resultados obtidos no campo dos xogos numéricos, ás veces profundos, números primos, números amigos, etc. e noutros casos só curiosidades. Seguiremos por esta última vía.
Paira empezar, por que non, colleremos o 142857 natural. Dá un número real e normal, como calquera outro. Con todo, non é certo. Multiplicando este número polo seis primeiros números naturais:
142857 x 1 = 142857 142857 x 2 = 285714 142857 x 3 = 428571 142857 x 4 = 571428 142857 x 5 = 714285 142857 x 6 = 857142
todos os produtos teñen as mesmas cifras, mantendo a orde das cifras coma se fose un ciclo. Se ademais multiplícase por 7:
142857 x 7 = 999.999
obtense. Este último resultado, cun pequeno esforzo, pódenos levar a coñecer a natureza do número. Se se calcula a expresión decimal do número racional 1/7,
0,142857 142857 142857 142857 ... (0,142857 142857... x 7 = =0,99999999...)
obtense, é dicir, o número 142857 inicial é o período do número 1/7.
Atopáronse outros números coas mesmas propiedades. Estes números denomínanse números cíclicos. Entre outros, os xerados polos números 17, 19, 23, 29, 47, 59, 61 e 97 menores de 100. Por exemplo, o número 17 produce a fracción 1/17, sendo o seu período 0588235294117647. Se multiplicas este número por 1, 2, ..., 16, obterás as mesmas cifras; no mesmo orde, pero empezando por outro número (non ceros):
0588235294117647 x 3 = 1764705882352941
Todos os números cíclicos son períodos das fraccións inversas de certos números primos.
Deixemos polo momento os números cíclicos e imos ver outros números. Probablemente moitos lectores coñezan o número 12345679 e as súas propiedades:
12345679 x 9 = 111 111 111 12345679 x 18 = 222 222 12345679 x 81 = 999 999 999
Con todo, non sabemos si coñeces ou non que o que aquí se cumpre paira o número 9 pódese encher noutros números. A continuación explicámosche como facelo. Calcularemos como exemplo outro paira o número 7. Expómolo como ecuación: nós queremos buscar o número x, que multiplicado por 7 daranos un número de 1 cifras, é dicir:
x . 7 = 111 111 111 ... (non coñecemos o número de cifras)
polo que paira buscar x hai que dividir o número 1111... por 7 ata que a división sexa exacta.
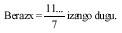
Se se realiza o cálculo

Neste caso o número de 1 cifras ten seis cifras. Este método demóstranos que paira o número 2 non é posible obter este número (nin sequera paira pares), xa que non é o número 111... e é divisible polo número 2.
Como curiosidade diremos que o número que se obtén paira o número 49 é o 2267573696145124716553287981859410430839.
Pasemos a outro.
Toma un número que non ten todas as cifras iguais. Nós eliximos 8161. O que imos facer aquí neste número debes repetilo co número que adiantaches.

O mesmo farase co número que aparece na conta
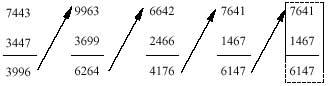
cando acaba? Na última dedución vese claramente cal é a resposta. Si na última dedución a diferenza ten as mesmas cifras que o minuendo e o restador, isto significa que si se reordenan as cifras obterase a mesma resta. Por tanto, non se pode seguir.
Que? Pasouche o mesmo co teu número? Se non estamos equivocados, conseguiches o mesmo número 6174, non?
O mesmo ocorre cos números de 3 cifras

Ao final sempre se obtén o 495.
Deixamos paira ti a análise dos números de dous e cinco cifras.
Paira terminar diremos que os resultados que teñades debaixo destas liñas non merecen outro nome que a curiosidade. No primeiro grupo todas as multiplicacións as cifras 1, 2, 3, 4, 5, 6, 7, 8 e 9 aparecen una soa vez:
138 x 42 = 5796 157 x 28 = 4396 159 x 48 = 7632 186 x 39 = 7254 198 x 27 = 5346 297 x 18 = 5346 483 x 12 = 5796 1738 x 4 = 6952 1963 x 4 = 7852
No segundo grupo os cadrados dalgúns números especiais:
1 2 = 1 11 2 = 121 111 2 = 12321 1111 2 = 1234321 11111 2 = 123454321 11111111 2 = 12345654321 11111111 2 = 1234567654321 1111 2 = 12345676765874321 1111111 2 2 = 12345678678987654321
9 2





