Números
Aquests conjunts es representen amb les lletres N, Z, Q, R, C respectivament, i compleixen que cadascun d'ells pertanyi al grup següent. Això sol dir-se matemàticament N\ Z Q Q B C.
Però tot això és una mera teoria, ja que en la realitat, al carrer, els números més utilitzats són els del grup Z i com a molt els del grup Q. De fet, els números tipus 1, 2, 1000, 3627 són els que més s'utilitzen i, per dir-ho d'alguna manera, si volem expressar els deutes, posem davant els números (–) en negatiu. Per descomptat, també s'utilitzen nombres decimals. Exemple 2,13 m, 7,14 kg. 1,8 l, etc. No obstant això, fusters, lampistes, etc. substitueixen el metre i el centímetre per mil·límetre com a unitat a l'hora d'indicar les mesures. Així, els nombres decimals es converteixen en simples: 2130 mm per exemple.
Aquest ús dels nombres naturals, a més de donar nom als números, ha portat a molts matemàtics a realitzar una profunda anàlisi dels mateixos i a tantes persones que no són matemàtiques. El fruit d'aquest aprofundiment és la teoria numèrica. Aquesta teoria amb el matemàtic Fermat XVII. Podem dir que va néixer en el segle XIX. En aquest segle, precisament, es va publicar el primer tractat sobre Jocs Matemàtics escrit pel poeta i cineasta Claude-Gaspard Bachet i Méziriac: Problemes plaisant detectables qui es font parell els nomenis. En ella, a més del joc de naips i números coneguts en aquella època, s'incloïen qüestions més profundes. Entre altres, la construcció de quadrats màgics i els problemes d'anàlisis il·limitades.
D'altra banda, hem de considerar com a fruit tant els resultats obtinguts en el camp dels jocs numèrics, a vegades profunds, nombres primers, números amics, etc. i en altres casos només curiositats. Seguirem per aquesta última via.
Per a començar, per què no, agafarem el 142857 natural. Dóna un nombre real i normal, com qualsevol altre. No obstant això, no és cert. Multiplicant aquest número pels sis primers nombres naturals:
142857 x 1 = 142857
142857 x 2 = 285714
142857 x 3 = 428571
142857 x 4 = 571428
142857 x 5 = 714285
142857 x 6 = 857142
tots els productes tenen les mateixes xifres, mantenint l'ordre de les xifres com si fos un cicle. Si a més es multiplica per 7:
142857 x 7 = 999.999
s'obté. Aquest últim resultat, amb un petit esforç, ens pot portar a conèixer la naturalesa del número. Si es calcula l'expressió decimal del nombre racional 1/7,
0,142857 142857 142857 142857 ... (0,142857 142857... x 7 = =0,99999999...)
s'obté, és a dir, el número 142857 inicial és el període del número 1/7.
S'han trobat altres números amb les mateixes propietats. Aquests números es denominen números cíclics. Entre altres, els generats pels números 17, 19, 23, 29, 47, 59, 61 i 97 menors de 100. Per exemple, el número 17 produeix la fracció 1/17, sent el seu període 0588235294117647. Si multipliques aquest número per 1, 2, ..., 16, obtindràs les mateixes xifres; en el mateix ordre, però començant per un altre número (no zeros):
0588235294117647 x 3 = 1764705882352941
Tots els números cíclics són períodes de les fraccions inverses de certs nombres primers.
Deixem de moment els números cíclics i veurem altres números. Probablement molts lectors coneixen el número 12345679 i les seves propietats:
12345679 x 9 = 111 111 111
12345679 x 18 = 222 222
12345679 x 81 = 999 999 999
No obstant això, no sabem si coneixes o no que el que aquí es compleix per al número 9 es pot emplenar en altres números. A continuació t'expliquem com fer-ho. Calcularem com a exemple altre per al número 7. Ho plantegem com a equació: nosaltres volem buscar el número x, que multiplicat per 7 ens donarà un número d'1 xifres, és a dir:
x . 7 = 111 111 111 ... (no coneixem el nombre de xifres)
pel que per a buscar x cal dividir el número 1111... per 7 fins que la divisió sigui exacta.
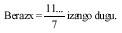
Si es realitza el càlcul

En aquest cas el número d'1 xifres té sis xifres. Aquest mètode ens demostra que per al número 2 no és possible obtenir aquest número (ni tan sols per a parells), ja que no és el número 111... i és divisible pel número 2.
Com a curiositat direm que el número que s'obté per al número 49 és el 2267573696145124716553287981859410430839.
Passem a un altre.
Presa un número que no té totes les xifres iguals. Nosaltres triem 8161. El que farem aquí en aquest número has de repetir-lo amb el número que has avançat.

El mateix es farà amb el número que apareix en el compte
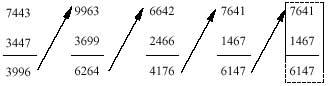
quan acaba? En l'última deducció es veu clarament quina és la resposta. Si en l'última deducció la diferència té les mateixes xifres que el minuend i el restador, això significa que si es reordenen les xifres s'obtindrà la mateixa resta. Per tant, no es pot seguir.
Què? T'ha passat el mateix amb el teu número? Si no estem equivocats, has aconseguit el mateix número 6174, no?
El mateix ocorre amb els números de 3 xifres

Al final sempre s'obté el 495.
Deixem per a tu l'anàlisi dels números de dues i cinc xifres.
Per a acabar direm que els resultats que tingueu sota aquestes línies no mereixen un altre nom que la curiositat. En el primer grup totes les multiplicacions les xifres 1, 2, 3, 4, 5, 6, 7, 8 i 9 apareixen una sola vegada:
138 x 42 = 5796
157 x 28 = 4396
159 x 48 = 7632
186 x 39 = 7254
198 x 27 = 5346
297 x 18 = 5346
483 x 12 = 5796
1738 x 4 = 6952
1963 x 4 = 7852
En el segon grup els quadrats d'alguns números especials:
1 2 = 1
11 2 = 121
111 2 = 12321
1111 2 = 1234321
11111 2 = 123454321 11111111
2 = 12345654321
11111111
2 = 1234567654321 1111 2 = 12345676765874321 1111111
2 2 = 12345678678987654321
9 2





