Números
Estos conjuntos se representan con las letras N, Z, Q, R, C respectivamente, y cumplen que cada uno de ellos pertenezca al grupo siguiente. Esto suele decirse matemáticamente N\ Z Q Q B C.
Pero todo esto es una mera teoría, ya que en la realidad, en la calle, los números más utilizados son los del grupo Z y como mucho los del grupo Q. De hecho, los números tipo 1, 2, 1000, 3627 son los que más se utilizan y, por decirlo de alguna manera, si queremos expresar las deudas, ponemos delante los números (–) en negativo. Por supuesto, también se utilizan números decimales. Ejemplo 2,13 m, 7,14 kg. 1,8 l, etc. Sin embargo, carpinteros, fontaneros, etc. sustituyen el metro y el centímetro por milímetro como unidad a la hora de indicar las medidas. Así, los números decimales se convierten en simples: 2130 mm por ejemplo.
Este uso de los números naturales, además de dar nombre a los números, ha llevado a muchos matemáticos a realizar un profundo análisis de los mismos y a tantas personas que no son matemáticas. El fruto de esta profundización es la teoría numérica. Esta teoría con el matemático Fermat XVII. Podemos decir que nació en el siglo XIX. En ese siglo, precisamente, se publicó el primer tratado sobre Juegos Matemáticos escrito por el poeta y cineasta Claude-Gaspard Bachet y Méziriac: Problemas plaisant detectables qui se font par les nombres. En ella, además del juego de naipes y números conocidos en aquella época, se incluían cuestiones más profundas. Entre otros, la construcción de cuadrados mágicos y los problemas de análisis ilimitados.
Por otro lado, debemos considerar como fruto tanto los resultados obtenidos en el campo de los juegos numéricos, a veces profundos, números primos, números amigos, etc. y en otros casos sólo curiosidades. Seguiremos por esta última vía.
Para empezar, por qué no, cogeremos el 142857 natural. Da un número real y normal, como cualquier otro. Sin embargo, no es cierto. Multiplicando este número por los seis primeros números naturales:
142857 x 1 = 142857 142857 x 2 = 285714 142857 x 3 = 428571 142857 x 4 = 571428 142857 x 5 = 714285 142857 x 6 = 857142
todos los productos tienen las mismas cifras, manteniendo el orden de las cifras como si fuera un ciclo. Si además se multiplica por 7:
142857 x 7 = 999.999
se obtiene. Este último resultado, con un pequeño esfuerzo, nos puede llevar a conocer la naturaleza del número. Si se calcula la expresión decimal del número racional 1/7,
0,142857 142857 142857 142857 ... (0,142857 142857... x 7 = =0,99999999...)
se obtiene, es decir, el número 142857 inicial es el periodo del número 1/7.
Se han encontrado otros números con las mismas propiedades. Estos números se denominan números cíclicos. Entre otros, los generados por los números 17, 19, 23, 29, 47, 59, 61 y 97 menores de 100. Por ejemplo, el número 17 produce la fracción 1/17, siendo su período 0588235294117647. Si multiplicas este número por 1, 2, ..., 16, obtendrás las mismas cifras; en el mismo orden, pero empezando por otro número (no ceros):
0588235294117647 x 3 = 1764705882352941
Todos los números cíclicos son periodos de las fracciones inversas de ciertos números primos.
Dejemos por el momento los números cíclicos y vamos a ver otros números. Probablemente muchos lectores conozcan el número 12345679 y sus propiedades:
12345679 x 9 = 111 111 111 12345679 x 18 = 222 222 12345679 x 81 = 999 999 999
Sin embargo, no sabemos si conoces o no que lo que aquí se cumple para el número 9 se puede rellenar en otros números. A continuación te explicamos cómo hacerlo. Calcularemos como ejemplo otro para el número 7. Lo planteamos como ecuación: nosotros queremos buscar el número x, que multiplicado por 7 nos dará un número de 1 cifras, es decir:
x . 7 = 111 111 111 ... (no conocemos el número de cifras)
por lo que para buscar x hay que dividir el número 1111... por 7 hasta que la división sea exacta.
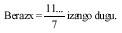
Si se realiza el cálculo

En este caso el número de 1 cifras tiene seis cifras. Este método nos demuestra que para el número 2 no es posible obtener este número (ni siquiera para pares), ya que no es el número 111... y es divisible por el número 2.
Como curiosidad diremos que el número que se obtiene para el número 49 es el 2267573696145124716553287981859410430839.
Pasemos a otro.
Toma un número que no tiene todas las cifras iguales. Nosotros elegimos 8161. Lo que vamos a hacer aquí en este número debes repetirlo con el número que has adelantado.

Lo mismo se hará con el número que aparece en la cuenta
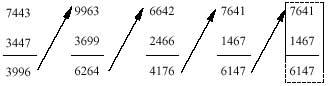
¿cuándo acaba? En la última deducción se ve claramente cuál es la respuesta. Si en la última deducción la diferencia tiene las mismas cifras que el minuendo y el restador, esto significa que si se reordenan las cifras se obtendrá la misma resta. Por lo tanto, no se puede seguir.
¿Qué? ¿Te ha pasado lo mismo con tu número? Si no estamos equivocados, has conseguido el mismo número 6174, ¿no?
Lo mismo ocurre con los números de 3 cifras

Al final siempre se obtiene el 495.
Dejamos para ti el análisis de los números de dos y cinco cifras.
Para terminar diremos que los resultados que tengáis debajo de estas líneas no merecen otro nombre que la curiosidad. En el primer grupo todas las multiplicaciones las cifras 1, 2, 3, 4, 5, 6, 7, 8 y 9 aparecen una sola vez:
138 x 42 = 5796 157 x 28 = 4396 159 x 48 = 7632 186 x 39 = 7254 198 x 27 = 5346 297 x 18 = 5346 483 x 12 = 5796 1738 x 4 = 6952 1963 x 4 = 7852
En el segundo grupo los cuadrados de algunos números especiales:
1 2 = 1 11 2 = 121 111 2 = 12321 1111 2 = 1234321 11111 2 = 123454321 11111111 2 = 12345654321 11111111 2 = 1234567654321 1111 2 = 12345676765874321 1111111 2 2 = 12345678678987654321
9 2





