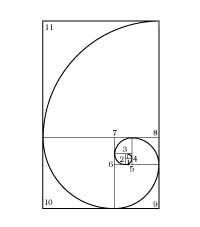
Número ouro
“... dúas cousas non se poden combinar sen terceiro, é necesario un vínculo que os une, e non hai mellor que uno mesmo e o que reúne, todo igual e único. E a natureza da proporción alcanza ese obxectivo, xa que de tres números, ou de tres masas, ou de calquera do tres forzas, a proporción con respecto ao último é a mesma que con respecto ao último, e, por outra banda, cando a proporción con respecto ao último é a mesma que co primeiro deles (o intermedio convértese no primeiro e o último no medio), todos permanecen intencionadamente igual que antes, formando parte dunha relación similar”.
Platón, “Conversacións, Timeo”
A orixe do número de ouro é antigo. Non se pode saber desde cando o home coñece (apika, harean pentagrama, makila sen levantar, que podía imaxinar desde que era consciente). Os exipcios xa o coñecían, pero foi Euclides quen o definiu:
“Un dereito está dividido na proporción entre as cabezas e a bisectriz cando a proporción entre a maior e a maior é a mesma entre esta e a menor”.
Por exemplo, na figura 1, a parte AA' é o segmento ouro ou sección do segmento AB,
AA' = A'BAB
= AA'
Cúmprese a proporción.
Se o lector non cre que comprobe una regra. Independentemente do segmento AB,
AA'
=A'B
? AB = AA' = ?o cociente que dá a sección de ouro toma sempre o mesmo valor:
d = 0,618033988
É un número algebraico irracional d cuxa expresión concreta é:
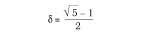
Este número sorpréndenos na Antigüedad, no Renacemento e na actualidade.
Mencionaremos dúas propiedades curiosas:
Si a d engadímoslle 1 ou lle damos a volta, obteremos o mesmo valor:
1 + ? = 1 / ? edo1
+ 0,618033... Restando = 1,618033 = 1 / 0,618033...1-i
? ou calculando ?2, obteremos o mesmo valor:1 – ?
= ?2 edo1 – 0,618033...
= 0,391966... = (0,618033...)2
Desde a antigüidade coñécense os métodos de división dun segmento en proporción áurea (1. irud. ). A proporción de ouro atópase tamén en moitas figuras xeométricas.
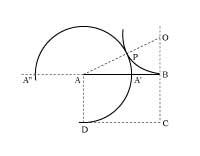
AB.Ademais, AB = =0,618033... x A”B, é dicir, AB A”B é a sección áurea do segmento.
O máis coñecido é o pentagrama (ou estrela de cinco vértices), símbolo máxico dos pitagóricos e alquimistas (2. irud. ). A pesar de que no Renacemento deuse una gran importancia á proporción de ouro, tanto en teoría como na práctica, non se utilizou por primeira vez no Renacemento. Pola contra, na pirámide de Keops (3. irud. ), Utilizouse xa no Partenón de Atenas, Catedral de Chartres, etc.
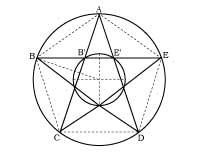
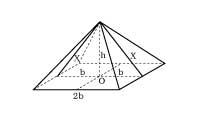
Figura . Segundo o geógrafo grego Herodoto, que describiu as pirámides exipcias, a altura h da pirámide de Keops é a metade da base b e a metade do apotema x. É dicir,
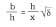
Isto significa que a sección áurea de b x e, por tanto, o perímetro da base é igual á lonxitude da circunferencia de altura h. Por esta razón hai quen cre que algúns exipcios coñecían o cadro do círculo. Non é necesario recorrer aos atlánticos ou marcianos. O segredo da gran pirámide radica nas súas dimensións de ouro:\
ª 4> ? aprox.
Tamén se atopa no propio corpo humano. Segundo o “canon” de Leonardo, as proporcións máis belas e armoniosas do corpo obtéñense cando están en proporción dourada. Leonardo meteu ao “home brillante” nun círculo cuxo centro é o mesmo e cuxo radio está nunha proporción dourada coa altura do home (4. irud. ).
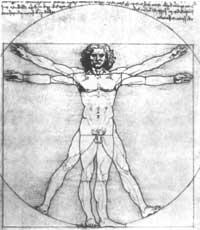
Os científicos do Renacemento adecuaban ao número de ouro o valor da lei universal da harmonía. Non se equivocaban, XVII. Segundo demostrou Kepler no século XX. As proporcións de ouro aparecen nas distancias entre planetas. O número de ouro indica cando un ano concreto corresponde a un ciclo lunar de 19 anos.
A sección áurea tamén se atopa na natureza e os seus fenómenos. Moitas veces atópanse flores e plantas con proporcións de ouro. Entre os animais tamén hai exemplos: a estrela da mar, a cuncha do fósil animado Nautilus (5. irud. ). O átomo de carbono, é dicir, os diamantes e o composto básico dos seres vivos, ten tamén una estrutura de ouro.