Número or
“... dues coses no es poden combinar sense tercer, és necessari un vincle que els uneix, i no hi ha millor que un mateix i el que reuneix, tot igual i únic. I la naturalesa de la proporció aconsegueix aquest objectiu, ja que de tres números, o de tres masses, o de qualsevol de les tres forces, la proporció respecte a l'últim és la mateixa que respecte a l'últim, i, d'altra banda, quan la proporció respecte a l'últim és la mateixa que amb el primer d'ells (l'intermedi es converteix en el primer i l'últim en el mitjà), tots romanen intencionadament igual que abans, formant part d'una relació similar”.
Plató, “Converses, Timeo”
L'origen del nombre d'or és antic. No es pot saber des de quan l'home coneix (apika, harean pentagrama, makila sense aixecar, que podia imaginar des que era conscient). Els egipcis ja ho coneixien, però va anar Euclides qui ho va definir:
“Un dret està dividit en la proporció entre els caps i la bisectriu quan la proporció entre la major i la major és la mateixa entre aquesta i la menor”.
Per exemple, en la figura 1, la part AA' és el segment oro o secció del segment AB,
AA' = A'BAB
= AA'
Es compleix la proporció.
Si el lector no creu que comprovi una regla. Independentment del segment AB,
AA'
=A'B
? AB = AA' = ?el quocient que dóna la secció d'or pren sempre el mateix valor:
d = 0,618033988
És un nombre algebraic irracional d l'expressió concreta de la qual és:
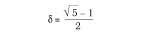
Aquest número ens sorprèn en l'Antiguitat, en el Renaixement i en l'actualitat.
Esmentarem dues propietats curioses:
Si a d li afegim 1 o li donem la volta, obtindrem el mateix valor:
1 + ? = 1 / ? edo1
+ 0,618033... Restant = 1,618033 = 1 / 0,618033...1-i
? o calculant ?2, obtindrem el mateix valor:1 – ?
= ?2 edo1 – 0,618033...
= 0,391966... = (0,618033...)2
Des de l'antiguitat es coneixen els mètodes de divisió d'un segment en proporció àuria (1. irud. ). La proporció d'or es troba també en moltes figures geomètriques.
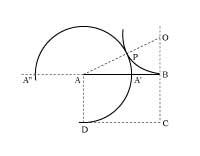
AB.A més, AB = =0,618033... x A”B, és a dir, AB A”B és la secció àuria del segment.
El més conegut és el pentagrama (o estrella de cinc vèrtexs), símbol màgic dels pitagòrics i alquimistes (2. irud. ). A pesar que en el Renaixement es va donar una gran importància a la proporció d'or, tant en teoria com en la pràctica, no es va utilitzar per primera vegada en el Renaixement. Per contra, en la piràmide de Kheops (3. irud. ), Es va utilitzar ja al Partenó d'Atenes, Catedral de Chartres, etc.
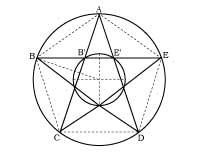
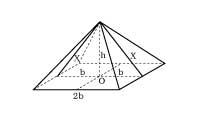
Figura . Segons el geògraf grec Heròdot, que va descriure les piràmides egípcies, l'altura h de la piràmide de Kheops és la meitat de la base b i la meitat de l'apotema x. És a dir,
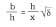
Això significa que la secció àuria de b x i, per tant, el perímetre de la base és igual a la longitud de la circumferència d'altura h. Per aquesta raó hi ha qui creu que alguns egipcis coneixien el quadre del cercle. No és necessari recórrer als atlàntics o marcians. El secret de la gran piràmide radica en les seves dimensions d'or:\
ª 4> ? aprox.
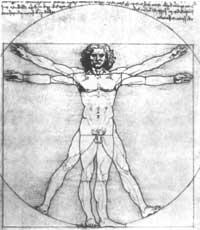
També es troba en el propi cos humà. Segons el “cànon” de Leonardo, les proporcions més belles i harmonioses del cos s'obtenen quan estan en proporció daurada. Leonardo va ficar al “home brillant” en un cercle el centre del qual és el mateix i el radi del qual està en una proporció daurada amb l'altura de l'home (4. irud. ).
Els científics del Renaixement adequaven al nombre d'or el valor de la llei universal de l'harmonia. No s'equivocaven, XVII. Segons va demostrar Kepler en el segle XX. Les proporcions d'or apareixen en les distàncies entre planetes. El nombre d'or indica quan un any concret correspon a un cicle lunar de 19 anys.
La secció àuria també es troba en la naturalesa i els seus fenòmens. Moltes vegades es troben flors i plantes amb proporcions d'or. Entre els animals també hi ha exemples: l'estrella de la mar, la petxina del fòssil animat Nautilus (5. irud. ). L'àtom de carboni, és a dir, els diamants i el compost bàsic dels éssers vius, té també una estructura d'or.