Gold Number
“... two things cannot be combined without a third, a bond that unites them is necessary, and there is no better than oneself and what brings together, all equal and unique. And the nature of proportion reaches that goal, since of three numbers, or three masses, or of any of the three forces, the proportion with respect to the latter is the same as with respect to the latter, and, on the other hand, when the proportion with respect to the latter is the same as with the first of them (the intermediate becomes the first and the last in the middle), all remain intentionally the same as before, forming part of a similar relationship.”
Plato, “Conversations, Timeo”
The origin of the gold number is ancient. One cannot know from when man knows (apika, harean pentagram, makila without lifting, which he could imagine since he was conscious). The Egyptians already knew him, but it was Euclid who defined him:
“A right is divided into the proportion between the heads and the bisector when the proportion between the greater and the greater is the same between the latter and the lesser.”
For example, in Figure 1, the AA part is the gold segment or AB segment section,
AA' = A'BAB
= AA'
The proportion is met.
If the reader does not believe that he checks a rule. Regardless of the AB segment,
AA'
=A'B
? AB = AA' = ?the quotient given by the gold section always takes the same value:
d = 0.618033988
It is an irrational algebraic number d whose concrete expression is:
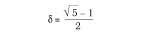
This number surprises us in Antiquity, in the Renaissance and today.
We will mention two curious properties:
If we add 1 to d or turn it around, we get the same value:
1 + ? = 1 / ? edo1
+ 0,618033... Subtracting = 1,618033 = 1 / 0,618033...1-i
? or calculating ?2, we will obtain the same value:1 – ?
= ?2 edo1 – 0,618033...
= 0.391966... = (0,618033...)2
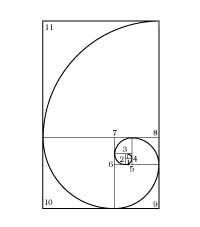
Since ancient times the methods of division of a segment in golden proportion (1. irud. ). The proportion of gold is also found in many geometric figures.
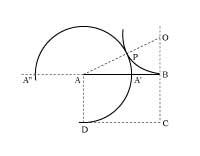
addition, AB = =0.618033... x A”B, i.e. AB A”B is the golden section of the segment.
The best known is the pentagram (or five-vertex star), magical symbol of the Pythagoreans and alchemists (2. irud. ). Although the proportion of gold was given great importance in the Renaissance, both in theory and in practice, it was not first used in the Renaissance. On the contrary, in the pyramid of Keops (3. irud. ), It was already used in the Parthenon of Athens, Cathedral of Chartres, etc.
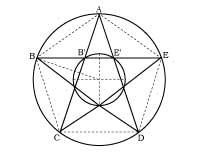
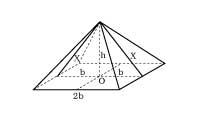
Figure . According to the Greek geographer Herodotus, who described the Egyptian pyramids, the height h of the pyramid of Keops is half of the base b and half of the apotopic x. That is,
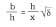
This means that the golden section of b x and therefore the perimeter of the base is equal to the length of the height circumference h. For this reason some believe that some Egyptians knew the circle picture. It is not necessary to resort to the Atlantic or Martian. The secret of the great pyramid lies in its golden dimensions:\
ª 4> ? approx.
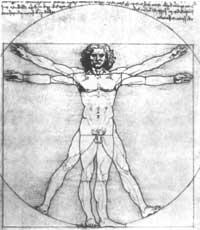
It is also found in the human body itself. According to Leonardo’s “canon”, the most beautiful and harmonious proportions of the body are obtained when they are in golden proportion. Leonardo put the “brilliant man” in a circle whose center is the same and whose radius is in a golden proportion with the height of man (4. irud. ).
Renaissance scientists adapted the value of the universal law of harmony to the golden number. They were not wrong, XVII. As Kepler demonstrated in the 20th century. The golden proportions appear in the distances between planets. The gold number indicates when a specific year corresponds to a lunar cycle of 19 years.
The golden section is also found in nature and its phenomena. Often there are flowers and plants with golden proportions. Among the animals there are also examples: the star of the sea, the shell of the animated fossil Nautilus (5. irud. ). The carbon atom, i.e., diamonds and the basic compound of living things, also has a gold structure.