Hasiera »   Erreportajeak »   Problema irekia

Problema aberto

• Zabaldu:
• Twitter
• Facebook
• Emaila

inquemos a circunferencia de diámetro 1. Ao seu ao redor representaremos polígonos inscritos e circunscritos que non serán normais.

Ramón Urkola propúxome este problema.

Fixemos una circunferencia de diámetro 1. Ao seu ao redor representaremos polígonos inscritos e circunscritos que non serán normais. Seguiremos o seguinte procedemento: representaremos o polígono circunscrito da zona k e calcularemos o seu _perímetro P0(k). No segundo _paso tomaremos este perímetro P0(k) como o número de lados dos novos polígonos inscritos e circunscritos e calcularemos os seus novos perímetros; P1(k) e P1(k); P1(k) como o número _de lados dos dous novos polígonos, P1(k) e P2(Pk). Continuando desta forma obtemos dúas secuencias de polígonos e os seus correspondentes perímetros:

Inscrita: P0, _p1(k), p2(k), ..., _pn(k), ...Circunscrita:
P0, _P1, P2, ..., _Pn(k), ...

Lembrar que _{cada Pn(k) ten} dous significados: o perímetro dun polígono circunscrito e o número de lados dos seguintes polígonos inscritos e circunscritos.

A pregunta é teñen límites estas dúas secuencias?.

Cabe destacar que os polígonos que aparecen aquí son “polígonos teóricos”. De feito, o perímetro _Pn(k) é un número real que non ten por que ser sempre un número normal. Por exemplo, mirando ao taboleiro, cando collemos k = 3,5950 aparécenos un polígono de 3,5950. Iso non é un polígono moi común, claro.

Nº(s) _de interiores3.01005,173,594,83,83,83,82,83,82,83,83,82,83,83,82,83,83,82,83,82,83,82,83,82,83,82,83,82,82,83,82,83,83,82,83,82,83,83,82,83,83,82,83,83,83,83,83,82,83,83,83,83,83,83,83,83,83,83,82,83,83,83,83,82,83,83,83,83,83,83,83,82,82,83,82,83,83,83,82,82,83,83,83,82,82,83,83,82,83,83,83,83,83,82,82,83,83,83,83,83,82,83,83,83,83,82,82,83,82,82,83,83,82,82,83,83,83,83,83,83,

Paira calcular o perímetro dos polígonos é necesario coñecer o ángulo central. Aproveitamos paira ampliar o concepto de polígono: os polígonos regulares de m (normal) poden dividirse en m triángulos isósceles, cun ángulo ? = 2p/m formado polas mesmas caras. Neste problema tomaremos o número m real.

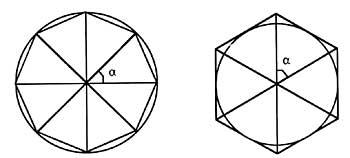
As fórmulas dos perímetros dos polígonos inscritos e circunscritos son: ángulo central correspondente aos polígonos ?; lonxitudes dos lados dos polígonos l; número de lados k e radio r.

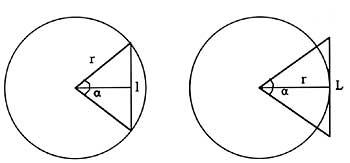
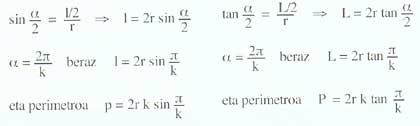
Ramón Urkola obtivo os datos que aparecen na táboa. O primeiro número de diferenzas que elixiu paira iniciar a secuencia foi k = 3,0100. A partir de aí _calcula os perímetros P0 = _2,6014 e P0 = 5,1718. Na seguinte k = 5,1718, obtendo p1 ₌ 2,9519 e P1 = _3,5950. Así conseguiu todos os seguintes perímetros.

Analizando a táboa obsérvase que a sucesión perimetral pn oscila ao redor de 2,82... O mesmo ocorre co perímetro Pn e o número 4. Iso dános a pista. 2,82... (ou máis concretamente 2) 2) e 4 son os límites de sérielas Pn _{e Pn?} En ambos os casos, os perímetros 2 e 4 corresponden a cadrados inscritos e circunscritos.

Nesta circunferencia, de diámetro 1, os perímetros dos polígonos inscritos diríxense cara ao valor 2, é dicir, obtense un polígono de 2 perímetros (número de lados). Este polígono é cadrado. Os perímetros dos polígonos circunscritos teñen como límite o valor 4. Este valor tamén corresponde a un cadrado. En ambos os casos as aproximacións prodúcense alternando valores máis ou menos aproximados (ver táboa).

A seguinte pregunta é que o diámetro da circunferencia está estreitamente unido aos perímetros dos polígonos. Por tanto, obteranse diferentes resultados paira distintos diámetros?, cal é a relación entre diámetro e límites?

Outra pregunta, si en lugar de tomar como número de lados os perímetros dos polígonos circunscritos os inscritos, que resultado obteriamos?.

Por último, pode ser calquera o número de primeiros lados que se elixa paira iniciar as secuencias de perímetros?.