Problème ouvert
Ramon Urkola m'a proposé ce problème.
Fixons une circonférence de diamètre 1. Autour de lui, nous représenterons des polygones inscrits et circonscrits qui ne seront pas normaux. Nous suivrons la procédure suivante : nous représenterons le polygone circonscrit de la zone k et calculerons son périmètre P0(k). Dans la deuxième étape nous prendrons ce périmètre P0(k) comme le nombre de côtés des nouveaux polygones inscrits et circonscrits et nous calculerons leurs nouveaux périmètres; P1(k) et P1(k); P1(k) comme le nombre de côtés des deux nouveaux polygones, P1(k) et P2(Pk). En continuant ainsi, nous obtenons deux séquences de polygones et leurs périmètres correspondants:
Inscrite : P0, p1(k), p2(k), ..., pn(k), ...Circonscrit:
P0, P1, P2, ..., Pn(k), ...
Rappelons que chaque Pn(k) a deux significations : le périmètre d'un polygone circonscrit et le nombre de côtés des polygones suivants inscrits et circonscrits.
La question est : ces deux séquences ont-elles des limites ?.
Il convient de noter que les polygones qui apparaissent ici sont “polygones théoriques”. En fait, le périmètre Pn(k) est un nombre réel qui ne doit pas toujours être un nombre normal. Par exemple, en regardant le tableau, quand nous prenons k = 3,5950, un polygone de 3,5950 nous apparaît. Ce n'est pas un polygone très commun, bien sûr.
83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,83,Pour calculer le périmètre des polygones, il faut connaître l'angle central. Nous en profitons pour élargir le concept de polygone: les polygones réguliers de m (normal) peuvent être divisés en m triangles isocèle, avec un angle ? = 2p/m formé par les mêmes faces. Dans ce problème, nous prendrons le nombre m réel.
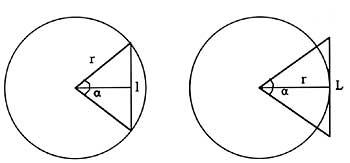
Les formules des périmètres des polygones inscrits et circonscrits sont : angle central correspondant aux polygones ? ; longueurs des côtés des polygones l ; nombre de côtés k et rayon r.
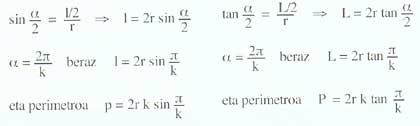
Ramón Urkola a obtenu les données qui apparaissent dans le tableau. Le premier nombre de différences que vous avez choisi pour lancer la séquence était k = 3,0100. À partir de là, il calcule les périmètres P0 = 2,6014 et P0 = 5,1718. Dans la suivante k = 5,1718, obtenant p1 = 2,9519 et P1 = 3,5950. Il a ainsi obtenu tous les périmètres suivants.
En analysant le tableau on observe que la succession périmétrique pn oscille environ 2,82... Il en va de même pour le périmètre Pn et le numéro 4. Cela nous donne la piste. 2,82... (ou plus précisément 2) 2) et 4 sont les limites des séries Pn et Pn? Dans les deux cas, les périmètres 2 et 4 correspondent à des carrés inscrits et circonscrits.
Dans cette circonférence, de diamètre 1, les périmètres des polygones inscrits sont dirigés vers la valeur 2, c'est-à-dire qu'on obtient un polygone de 2 périmètres (nombre de côtés). Ce polygone est carré. Les périmètres des polygones circonscrits ont pour limite la valeur 4. Cette valeur correspond également à un carré. Dans les deux cas, les approximations se produisent en alternant des valeurs plus ou moins approximatives (voir tableau).
La question suivante est que le diamètre de la circonférence est étroitement lié aux périmètres des polygones. Donc, différents résultats seront-ils obtenus pour différents diamètres?, Quel est le rapport entre diamètre et limites?
Une autre question, si au lieu de prendre comme nombre de côtés les périmètres des polygones circonscrits les inscrits, quel résultat obtiendrons-nous?
Enfin, n'importe quel nombre de premiers côtés peut être choisi pour commencer les séquences de périmètres?.





