Problema obert
Ramón Urkola em va proposar aquest problema.
Fixem una circumferència de diàmetre 1. Al seu al voltant representarem polígons inscrits i circumscrits que no seran normals. Seguirem el següent procediment: representarem el polígon circumscrit de la zona k i calcularem el seu perímetre P0(k). En el segon pas prendrem aquest perímetre P0(k) com el nombre de costats dels nous polígons inscrits i circumscrits i calcularem els seus nous perímetres; P1(k) i P1(k); P1(k) com el nombre de costats dels dos nous polígons, P1(k) i P2(Pk). Continuant d'aquesta forma obtenim dues seqüències de polígons i els seus corresponents perímetres:
Inscrita: P0, p1(k), p2(k), ..., pn(k), ...Circumscrita:
P0, P1, P2, ..., Pn(k), ...
Recordar que cada Pn(k) té dos significats: el perímetre d'un polígon circumscrit i el nombre de costats dels següents polígons inscrits i circumscrits.
La pregunta és tenen límits aquestes dues seqüències?.
Cal destacar que els polígons que apareixen aquí són “polígons teòrics”. De fet, el perímetre Pn(k) és un nombre real que no té per què ser sempre un número normal. Per exemple, mirant al tauler, quan agafem k = 3,5950 ens apareix un polígon de 3,5950. Això no és un polígon molt comú, clar.
Núm.(s) d'interiores3.01005,173,594,83,83,83,82,83,82,83,83,82,83,83,82,83,83,82,83,82,83,82,83,82,83,82,83,82,82,83,82,83,83,82,83,82,83,83,82,83,83,82,83,83,83,83,83,82,83,83,83,83,83,83,83,83,83,83,82,83,83,83,83,82,83,83,83,83,83,83,83,82,82,83,82,83,83,83,82,82,83,83,83,82,82,83,83,82,83,83,83,83,83,82,82,83,83,83,83,83,82,83,83,83,83,82,82,83,82,82,83,83,82,82,83,83,83,83,83,83,.Per a calcular el perímetre dels polígons és necessari conèixer l'angle central. Aprofitem per a ampliar el concepte de polígon: els polígons regulars de m (normal) poden dividir-se en m triangles isòsceles, amb un angle ? = 2p/m format per les mateixes cares. En aquest problema prendrem el número m real.
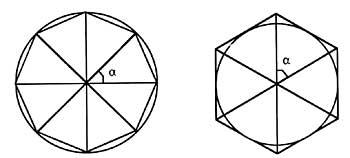
Les fórmules dels perímetres dels polígons inscrits i circumscrits són: angle central corresponent als polígons ?; longituds dels costats dels polígons l; nombre de costats k i radio r.
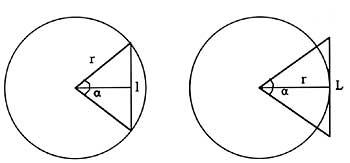
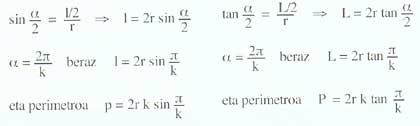
Ramón Urkola va obtenir les dades que apareixen en la taula. El primer nombre de diferències que va triar per a iniciar la seqüència va ser k = 3,0100. A partir d'aquí calcula els perímetres P0 = 2,6014 i P0 = 5,1718. En la següent k = 5,1718, obtenint p1 = 2,9519 i P1 = 3,5950. Així va aconseguir tots els següents perímetres.
Analitzant la taula s'observa que la successió perimetral pn oscil·la al voltant de 2,82... El mateix ocorre amb el perímetre Pn i el número 4. Això ens dóna la pista. 2,82... (o més concretament 2) 2) i 4 són els límits de les sèries Pn i Pn? En tots dos casos, els perímetres 2 i 4 corresponen a quadrats inscrits i circumscrits.
En aquesta circumferència, de diàmetre 1, els perímetres dels polígons inscrits es dirigeixen cap al valor 2, és a dir, s'obté un polígon de 2 perímetres (nombre de costats). Aquest polígon és quadrat. Els perímetres dels polígons circumscrits tenen com a límit el valor 4. Aquest valor també correspon a un quadrat. En tots dos casos les aproximacions es produeixen alternant valors més o menys aproximats (veure taula).
La següent pregunta és que el diàmetre de la circumferència està estretament unit als perímetres dels polígons. Per tant, s'obtindran diferents resultats per a diferents diàmetres?, quina és la relació entre diàmetre i límits?
Una altra pregunta, si en lloc de prendre com a nombre de costats els perímetres dels polígons circumscrits els inscrits, quin resultat obtindríem?.
Finalment, pot ser qualsevol el nombre de primers costats que es triï per a iniciar les seqüències de perímetres?.





