"(3) Isaac Newton, earth and heaven
Annus mirabilis
At Cambridge, Newton had to learn works by Aristotle and ruling natural philosophers, an inappropriate environment for carrying out his scientific revolution. But in 1665 the epidemic came to England and Newton left the university of Cambridge, returning to Woolsthorpe, his hometown. In it, apart from student functions, he gave many proofs of his creativity, such as the investigation of flows, the nature of light and gravitation. In fact, like many other scientists, he pursued the circular motion and came to find the law of centripetal force.
By then Huygens had already solved this problem, but Newton did not know it. This independent discovery followed the next process, imagining a ball moving on the inner surface of a hollow sphere: according to the principle of inertia that I knew beforehand, the ball tends to travel the right path, but as it moves in a circular way, it can come to the conclusion quoted in his words: all the bodies that move in a circular way suffer a central thrust. Quantitatively Newton was also able to mathematically express this force, i.e. F V 2 /R.
On the other hand, years later he recognized that in the pastures of his hamlet he was very interested, and that the fall of an apple prompted to think how the gravity of the Earth could reach the orbit of the Moon. The apple, having history or lying, is another thing: Although Gauss favored metaphor, it is true that Newton mentioned it.
As we move away from the center of the Earth (both in the higher constructions and in the higher mountains), gravity influences, why will it not extend to the orbit of the Moon? Newton concluded that the reason the Moon stays in its orbit was the same. And the law of circular motion and Kepler's third (R 3 /T 2 = kte) which was used for the case of the sun and planets! combining:
F V 2 /R = 4 . 2R 2 /T 2 . R = 4 . 2 /R 2 . [R 3 /T 2]
Therefore, F R -2 found the law of the inverse square of distance, although for the case of the Sun and the planets, and for the Earth and the Moon moving around it.
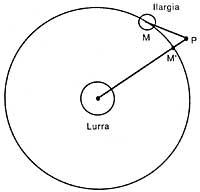
Therefore, he compared the force necessary to keep the Moon in its orbit with the force of gravity existing on the surface of the Earth (through the distances in which the Moon and a body detached from the hand are attracted to the Earth), finding very close results, but not so close as to be sure of the reason.
Why didn't those results fit? For it is often said that the difference between theory and observation was due to a poor measurement of terrestrial radio. However, by this disinterested measure, he concluded that another factor, the Cartesian vortex, should intervene. At the age of 23-24, Newton took the first step in obtaining the key to the Universe. However, these thoughts did not quickly reach the scientific society, and the error we have referred to pushed Newton to abandon these investigations until 1679.
With Hooke
In November 1679, as secretary of the Royal Society, Hooke, trying to forget the conflicts with Newton, sent him a letter with his analysis of planetary motion. Newton did not want to answer, but nevertheless, he described to Hooke an experiment to demonstrate the rotation of the Earth: a free-falling body from a tower; as the tangential velocity of the top of the tower is greater than that of the base, the body will deviate eastward (following the path of the spiral form) toward the center of the Earth. Hooke realizes the error: he believes that the path of the body would be similar to the ellipsoid.
Thus, until then Newton did not realize that the body falling under these conditions was subject to the principles of orbital motion. In this case Hooke's intuition was imposed and surprises Newton. He, angry at the mistake, wanted to correct Hooke's idea under the hypothesis of uniform gravity. Newton thundered again and full of voters, Hooke told him that gravity was inversely proportional to the square of distance.
Years later, this letter brought numerous allegations of Hooke's plagiarism to Newton when "Principia" was published. However, he recognized Halley that Hooke's correction of the spiral forced Newton to find the key to orbital motion. Therefore, using the method of limite and infinitesimal, I deduced: Kepler's second law was equivalent to the central force and the ellipse form forced that force to be inversely proportional to the square of the distance, definitively solving the problem of orbits.
In 1680, Newton, not having liked anything that was directed by Hooke, broke again the dessert with him, to the point of not being able to reach the concept of universal gravitation, which only acted with orbital dynamics.
Universal recording and " Principia "
In August 1684, Edmond Halley went to Cambridge to visit Newton. Halley asked Newton what was the shape of the planets around the Sun. Newton knew the correct answer (because he showed it): the ellipse. When he did not find the papers requested by Halley, three months later he sent him the work entitled "De motu corporum in gyrum". Not only with the resolution of the original problem, but also with the mathematical seeds of a general science of dynamics. This work was presented in December of the same year at the Royal Society.

In the next two years, included in the tireless creative sirimol, Newton, from the book "De motu ", wrote his masterpiece "Philosophiae Naturalis Principa Mathematica", the highest basic work of modern science. In April 1686 the manuscript of book I was presented at the Royal Society, and its members decided to print the book immediately. The truth is that Halley himself had to advance the money to print, being amanuense of the Association. Apart from that, Halley informed Newton of Hooke's complaint.
In fact, this denunciation had not much foundation: on the one hand, Hooke did not come up with the concept of current universal gravitation, and on the other, (let's remember the years of the epidemic) the inversion law of the square of distance that Newton found long before Hooke. Besides all this, in order to adequately reflect this system, great power mathematics (Newton's analysis) was needed, and Hooke's only provision consisted of an incredible unlimited intuition, nothing more. Furious, Newton cleaned all of Hooke's quotes from his book and, more seriously, III. threatened those who did not publish the book. For the happiness of science, Halley convinces her. To prevent Newton from breaking his magnificent treatise, culminating the printing process in July 1687, Samuel Pepys, director of the Royal Society, signed the " imprimatur ".
As has been said, it was divided into three books "Principia". In the first, after some definitions of great importance to strengthen dynamics, Newton presented three famous laws:
- Law I: "Every body remains at rest or in a state of uniform and direct motion, unless the printed forces modify it." Newton himself acknowledged that he took this principle of Galileo to reshape it in his system.
- II. law: " the change of movement is proportional to the printed motor force and is performed in the straight line direction in which it is printed ". In this case he also lent the idea to Galileo developing to unknown limits, especially with the description of centripetal forces.
- III. law: " there is always an equal reaction for each action. The interactions of two bodies are always equal and directed towards the opposite parties." This law, unlike the previous two, was completely new. The concept of universal gravitation was already in Newton's head: according to this law, gravitation could not be reduced only to the Solar System, but all planets, satellites, comets and stars had to move under this law.
Nevertheless, in a logical way they were collecting all the parts of the "puzzle". For example, the exact measurement of the radius that so much burukomin gave to Newton that Picard had made (which, as has been written on numerous occasions, became so nervous in the hands of Newton that, with nervousness, he could not redo the ancient calculus and had to perform it an assistant).

On the other hand, book I, XII. In paragraph (b), he was able to demonstrate that the gravitational pull of a sphere occurs when the entire mass of the sphere was in the mass centre, using a very elegant demonstration (even Newton was fascinated by it).
II. Just as Descartes rejected Aristotle's philosophy, Newton destroys the theory of "violent Cartesians." For example, LII. In proposition, this theory demonstrated that it cannot comply with Kepler's laws: that is, the internal circular motion in violent roaring fluids, under gravity, would become a spiral path, so the planets would touch the Sun. Medieval Christian theology fell down.
III. VII of the book in proposition, Newton presented his most famous discovery; the law of universal gravitation " gravitatem in corpora universa fieri, eamque proportionalem esse quantitati materiae in singulis ". That is, there is a force of gravity that corresponds to all bodies; proportional to the amount of mates they have. In today's words, "the gravitational interaction that occurs between two bodies is expressed by two equal attractive forces, directly proportional to their masses and inversely proportional to the square of the distance between both" (General Physics (II) U.S. Department of Physics. ). Quantitatively we can write as:
F = G . m 1 m 2 /e 2
where m1 and m2 are the masses of both bodies, r the distance between them and G the gravitational constant.
Through this law, Newton democratized ", destroying the hierarchy for celestial bodies invented until then. Being his useful instrument in his hands, Newton had a great advantage in explaining a series of misunderstood phenomena over the centuries:
- Tidal fluctuations, relating the gravitational effects of the Sun and the Moon on the seas.
- Based on the mass of the Earth, it opened the way to the solar and planetary masses.
- He pointed out the reason for the modification of the axis of rotation of the planets, clarifying the precession of the equinoxes.
- Due to the rotation, he predicted that the axes of the planets are inferior to the diameters perpendicular to them.
- As for the comets, leaving the hypothesis that their trajectory is correct, I deduced that they meet a conical line. He added to the comet of 1680 his parabolic orbit, and in the following years, Halley, using Newton's theory, pointed to the real path of his comet, ellipse of great eccentricity, with an approximate period of 75 years.
Recent years

Having exhausted his creative ability, Newton made no significant contribution after the publication of the "Principia". In other tasks, he insisted on setting the exact position of the Moon taking into account the attractions of the Sun and Earth. For this, he had several problems with the director of the Royal Observatory, Flamsteed, who was forced to use the results of his observations on the positions of the Moon, taking advantage of his great power against Flamsted's desire to achieve them. He came to explain some of the aberrations of our planet, but, of course, it was impossible for him to determine the exact position of the Moon ("in five or six equations," as he wanted); the problem of the three bodies is impossible to solve.
Finally, we will say that Newton's influence, both scientifically and philosophically, would be very important. The concept of science he built lasted until the arrival of Einstein. Euler, Lagrange, Hamilton and other scientists, drinking from their source, shone Newton's system. Astronomer Herschel discovered Uranus, etc. After all, one could appreciate Newton's breath, illuminating the path...





