"Principia" 300 años (2) Isaac Newton, creador del cálculo
Caminando

La Matemática griega, basada en gran medida en la Geometría, parece normal que se quiera calcular la superficie de las figuras planas y el volumen de los sólidos. Del mismo modo, al dar los primeros pasos de la Física mostraron interés por conseguir un centro de gravedad. La mayor parte de estos problemas se deben a Arquímedes, un sirviente (a. C.). III. En el siglo XIX): superficies de elipses y segmentos parabólicos, volumen de muchos sólidos de revolución (esfera, elipsoide, segmento de paraboloides, etc.) y el centro de gravedad de la mayoría, por ejemplo.
Pero Arquímedes no tenía la formulación fácil que ofrece el Cálculo actual (la integral de una sola función da lugar a varias resulsiones de Arquímedes) y cada problema era nuevo para él. Para la obtención de los resultados se valió de su intuición geométrica, descomponiendo a menudo la imagen en fragmentos muy pequeños y aproximando éstos por figuras conocidas (triángulos, cuadrados, cilindros). Posteriormente, para justificarlo, utilizaba el "método exhacutivo" adoptado por Eudel.
Pronto las Matemáticas (al menos las relacionadas con el cálculo) quedaron dormidas y con ella los trabajos de Arquímedes. Los árabes trajeron estas obras al oeste de Europa, donde fue el XVI. En el siglo XX retomaron su estudio. XVII. Se puede decir que a principios del siglo XX se entendían las obras de Arquímedes, al menos lo suficiente para dar nuevos frutos. En esos cincuenta años hasta llegar a Newton se acumularon nombres y rescatados: Kepler, Cavalieri, Torricelli, Roberval, Descartes, Fermat, Pascal, Wallis, Barrow, etc.
De la mano de Descartes, la Geometría Analítica tuvo una gran influencia en el Cálculo, ya que la expresión algebraica de las curvas provocó una nueva y ágil formulación de problemas. Un paso importante fue el de la clasificación de problemas, con dos grandes grupos: los problemas de tangentes y los problemas de superficies, que los reciben de los modelos principales. Los problemas del primer grupo (rectificar una curva en un punto o calcular los máximos y mínimos) eran prácticamente nuevos, ya que en las Matemáticas antiguas no aparecen y se resuelven mediante la derivada. Los del segundo grupo, sin embargo, son formulados por Arquímedes y hoy los asociamos a la integración.
Entre los matemáticos arriba mencionados, Fermat fue el más avanzado en la resolución de estos problemas. Para el cálculo de máximos y mínimos, por ejemplo, dio el siguiente método: Hallar el valor A para el que [F(A + E) - F (A)] / E = 0, haciendo E = 0 (una vez obtenido el cociente). Aunque parezca un derivado, aquí no hay límite, ya que Fermat lo hace para polinomios, donde el cociente es siempre exacto. En integración, hoy
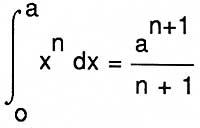
conocía el equivalente geométrico de la fórmula, algo demostrado en Cavalieri, Pascal o Roberval.
Y llegó Newton
El joven Newton conoció y pronto dominó las técnicas de los libros de Matemáticas leyendo su propio libro. Esta formación autodidáctica no es sorprendente, teniendo en cuenta que en las Universidades no se impartían cursos ordinarios sobre este tema. En todo caso, contaría con la colaboración de Barrow, tanto en la selección de libros como en el curso que éste impartió durante un año. Sin embargo, es conocido que pasaron de la mano de Newton de entonces y que tuvo una gran influencia de dos: La Geometría de Descartes y la de los libros "Arithmetica Infinitorum" de Wallis.
Pero Newton se adelantó a todos en 1665-66 años, ya que hasta entonces había visto como nadie la clave de los problemas y la solución era dar una regla para hacer la derivada, demostrar que la integral era la inversa de la derivada e indicar la vía de aplicación en diferentes problemas.
Newton medía todas las cantidades variables respecto al tiempo (más tarde dijo que el tiempo es cualquier cantidad que cambia uniformemente): eran fluentes. Las velocidades de cambio se denominaban flujos. Una curva laun es debida al movimiento de la abscisa y la ordenada y tanto x como y tienen sus flujos x e y. Dada la ecuación de la curva, se busca la relación entre los flujos. ¿Cómo lo conseguirá? Sustituir x e y por x + x o e y + y o en la ecuación de la curva para acortar la inicial, dividir por o y hacer 0 esta o. El método, además del estilo, es el actual, con la posibilidad de realizar una derivada implícita.
Por ejemplo, para derivar y = x m/n, aplica su método a la relación yn = xm: Después de tratar ambos lados de la igualdad (y + y o ) n = (x + x o ) m con la fórmula del binomio, tras dividir y n y x m eliminados por o, y anular dicho o, obtiene n y n-1 y = m x m-1 x. Basta con sustituir y por x m/n,
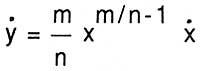
para tener una derivada conocida.
El teorema básico del cálculo o la inversa de la integración y la derivación, fue formulado geométricamente por Barrow en el libro " Lectiones Geometricae" (publicado en 1670), pero no parece que se apropiara de su valor. "La fórmula de Newton-Leibniz" es su presentación más sencilla: Si F' = f,
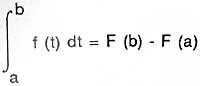
o bien,
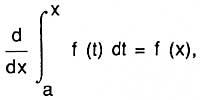
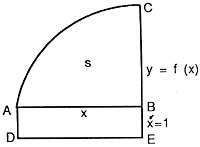
es decir, la derivada de la abscisa de la superficie es función (u ordenada). Veamos la formulación de Newton. Biz y = f (x) curva y s = superficie (ABC) (ver figura), que se genera por el movimiento paralelo de la recta vertical BC. Biz x = AB y hagamos el paralelogramo ABED considerando AD = 1. Entonces x = superficie (ABDE), esta superficie es generada por el movimiento de la VE. La relación de velocidades de incremento de ambas superficies, según Newton, es igual a la relación BC y BE, es decir, s/x = BC/BE = f(x).
Una vez decidido esto, al ser más fácil derivar, la tabla de integrales contendrá las derivadas al revés. De este modo, sin embargo, muchas curvas aún no pueden integrarse y siguiendo una idea tomada de Wallis para ampliar las posibilidades, consideró los desarrollos seriados de las funciones y los siguió para conseguir una nueva serie de temas integrados (sin hacer caso a los problemas de convergencia, por supuesto).
La expansión de (1 + x) m, cuando m es total, aunque se llama binomio de Newton, resulta realmente interesante cuando m es incompleto, entonces el polinomio no es una serie infinita. m en medio de dos números enteros (1/2, 3/2, ...) ya se debe a Newton la respuesta del caso, ya que demostró que se aplica la misma regla que los coeficientes de los polinomios para los coeficientes.
Con el objetivo de basarse en lo que se estaba haciendo, Newton hará referencia a las relaciones de los incrementos: flujo " la primera relación de los incrementos emergentes " o " la última relación de los incrementos fungibles ". A la vista de la imagen, supongamos que avanzamos un poco la abscisa, entonces la superficie aumenta y hay que conseguir una relación entre los incrementos de superficie y abscisa, pero la primera relación fluye es ", antes de comenzar a moverse ... Así mismo, considerando el proceso hacia atrás, los incrementos desaparecen y la última relación de incrementos destructivos " es el flujo. Se puede suscitar la idea de límite indeterminado.
Hay que compartir los honores
Entre las obras de Newton, las relacionadas con el Cálculo son: "De Analysi per Aequationes Numero Terminorum Infinitas" (escrito hacia 1669, publicado en 1711), " Methodus Fluxionum et Serierum Infinitorum" (escrito en 1671, publicado en 1736), " Tractatus de Quadratura Curvarum" (escrito en 1693, páginas 1704) y "principi" (pp. Como se ve, pasaron veinte años entre la obtención de los rescatados y su despido, y así, en 1675, Leibniz llegó por su parte a parecidos. El primer artículo de Leibniz se publicó en 1684, anticipándose durante tres años a "Principia".
En 1698 Fatio de Duillier, amigo de Newton, publicó un libro en el que le reconoció todo el mérito denunciando que Leibniz había hecho plagio. Leibniz se defendió a sí mismo y pasaron diez años hasta que el segundo ataque llegó en un artículo de Keill. Este artículo salió en la revista de la Real Sociedad y Leibniz, como asociado, solicitó en 1711 al secretario que aclarase el problema.
Cuando el presidente era Newton, se nombró un comité y la decisión de la comisión fue aún más dura para Leibniz. Además, decidieron publicar la colección de cartas "Commercium Epistolicum" contra Leibniz. El debate se agrandó y algunas personas de Leibniz se dieron cuenta de algunos errores de Newton. Leibniz, en 1714, escribió el programa " Historia et origo Calculi differentialis " para contar su verdad. A pesar de su muerte dos años después, Newton siguió atacando.
XX. Hasta el siglo XIX este punto ha estado sin decidir, pero cuando se han analizado los manuscritos de Leibniz se le ha reconocido definitivamente su mérito y hoy a ambos les corresponde el honor de ser creadores del Cálculo. El debate, sin embargo, afectó más a Inglaterra, donde los matemáticos locales y los del continente se alejaron y el desarrollo del Cálculo se produjo casi en su totalidad en la línea de Leibniz.
Nuevos caminos y bases sólidas
La difusión del cálculo resultó muy ágil gracias a las revistas de reciente creación. Sólo en la revista "Acta Eruditorum" hay más de un centenar de artículos en Leibniz desde el primero hasta los veinticinco años siguientes, la mayoría escritos por el propio Leibniz y los hermanos Bernouilli. XVIII. En el siglo XVIII el Cálculo llegaría a la cima con numerosos métodos y aplicaciones, en los que el nombre de Euler debe situarse muy por encima de sus contemporáneos. Junto a él destacan la segunda generación de bernouillitos, D'Alembert y, más tarde, Lagrange.
Pero el Calculo tenía un pecado original y el obispo inglés Berkeley lo denunció con dureza en 1735, en su libro " The Analyst ": las últimas relaciones de las cantidades devastadoras de Newton que se mencionaban en la base del razonamiento " y los "infinitesimales" de Leibniz eran inaceptables por parte de la reina. En palabras de Berkeley: "Lo que puede engullir el segundo o tercer flujo y el segundo o tercer diferencial no debería preocuparse, en mi opinión, de los problemas de la Divinidad ", es decir, uno y otro son cuestiones de fe. Eso sí, no cuestiona los resultados obtenidos.
A pesar de que cien años antes Cavalieri había escrito "el error es un problema de los filósofos y no de los matemáticos", los matemáticos que trataron de construir el Cálculo en bases sólidas, es destacable la importancia dada por D'Alembert al concepto de limite para la "Encyclopedie". XIX. A principios del siglo XX Bolzano, Praga y Cauchy, dieron una definición adecuada del límite en París (equivalente al que existe en cualquier libro de hoy) y a partir de él se define la derivada.
La integral, con Cauchy, pasó de ser la inversa de la derivada a definirla mediante un limite y entonces tuvo que demostrar la inversa entre ambas. La Integral siguió su propio camino y creó la llamada Teoría de la Medida; Lebesgue XX. Lo que terminó a principios del siglo XX. Además de la definición general de la integral, logró el teorema de diferenciación, la formulación moderna del teorema de Newton-Leibniz.





