"Beginner" 300 years (2) Isaac Newton, creator of calculus
Walking on foot

Greek Mathematics, based largely on Geometry, seems normal to want to calculate the surface of flat figures and the volume of solids. Similarly, when taking the first steps of Physics, they showed an interest in getting a center of gravity. Most of these problems are due to Archimedes, a servant (a. C.). III. In the 19th century): surfaces of ellipses and parabolic segments, volume of many solids of revolution (sphere, ellipsoid, paraboloid segment, etc.) and the center of gravity of the majority, for example.
But Archimedes did not have the easy formulation offered by the present Calculus (the integral of a single function gives rise to several results of Archimedes) and every problem was new to him. To obtain the results, he used his geometric intuition, often decomposing the image in very small fragments and approaching these by known figures (triangles, squares, cylinders). Later, to justify it, he used the "exhacutive method" adopted by Eudel.
Soon the Mathematics (at least those related to the calculus) were dormant and with it the works of Archimedes. The Arabs brought these works to the west of Europe, where it was the XVI. In the twentieth century they retook their study. XVII. It can be said that at the beginning of the twentieth century the works of Archimedes were understood, at least enough to bear new fruits. In those fifty years until reaching Newton were accumulated names and rescued: Kepler, Cavalieri, Torricelli, Roberval, Descartes, Fermat, Pascal, Wallis, Barrow, etc.
By the hand of Descartes, Analytical Geometry had a great influence on Calculus, since the algebraic expression of curves caused a new and agile formulation of problems. An important step was the classification of problems, with two large groups: the problems of tangents and the problems of surfaces, which receive them from the main models. The problems of the first group (rectifying a curve in a point or calculating the maximum and minimum) were practically new, since in ancient Mathematics they do not appear and are solved by the derivative. Those of the second group, however, are formulated by Archimedes and today we associate them to integration.
Among the above mentioned mathematicians, Fermat was the most advanced in solving these problems. For the calculation of maximum and minimum, for example, he gave the following method: Find the value A for which [F(A + E) - F (A)] / E = 0, making E = 0 (once obtained the quotient). Although it seems like a derivative, here there is no limit, since Fermat does it for polynomials, where the ratio is always accurate. In integration, today
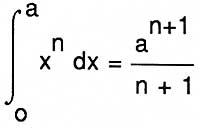
I knew the geometric equivalent of the formula, something shown in Cavalieri, Pascal or Roberval.
And Newton came
The young Newton met and soon mastered the techniques of the books of Mathematics by reading his own book. This self-teaching training is not surprising, taking into account that no ordinary courses were given in the universities on this subject. In any case, he would have the collaboration of Barrow, both in the selection of books and in the course he gave during a year. However, it is known that they passed from the hand of Newton of that time and which had a great influence of two: The Geometry of Descartes and the book "Arithmetica Infinitorum" by Wallis.
But Newton advanced to all in 1665-66 years, since until then he had seen as no one the key to problems and the solution was to give a rule to make the derivative, prove that the integral was the inverse of the derivative and indicate the way of application in different problems.
Newton measured all variable amounts over time (he later said time is any amount that changes uniformly): they were fluent. The speed of change was called flows. A laun curve is due to the motion of the abscisa and the orderly and both x and y have their flows x e and y. Given the equation of the curve, the relationship between flows is sought. How will you get it? Replace x e and x + x or e and + and or in the equation of the curve to shorten the initial, divide by or and make 0 this o. The method, in addition to the style, is the current one, with the possibility of performing an implicit derivative.
For example, to derive y = x m/n, apply your method to the relation yn = xm: After treating both sides of the equality (and + and o ) n = (x + x or ) m with the formula of the binomial, after dividing and n and x m eliminated by or, and annular said o, obtains n and n-1 and = m x m-1 x. Just replace and by x m/n,
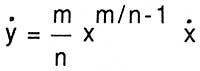
to have a known derivative.
The basic theorem of the calculus or inverse of integration and derivation, was geometrically formulated by Barrow in the book "Lectiones Geometricae" (published in 1670), but it does not seem to appropriate its value. "The formula of Newton-Leibniz" is its simplest presentation: Yes F' = f,
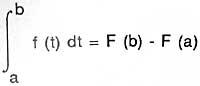
Or else,
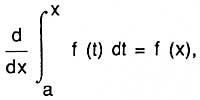
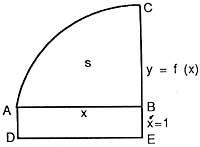
That is, the derivative of the abscisa of the surface is function (or ordered). Let's look at Newton's formulation. Biz y = f (x) curve and s = surface (ABC) (see figure), which is generated by the parallel movement of the vertical line BC. Biz x = AB and make the ABED parallelogram considering AD = 1. Then x = surface (ABDE), this surface is generated by the movement of the VE. The increase velocity ratio of both surfaces, according to Newton, is equal to the ratio BC and BE, i.e., s/x = BC/BE = f(x).
Once decided this, being easier to derive, the board of integrals will contain the derivatives to the reverse. In this way, however, many curves can still not be integrated and following an idea taken from Wallis to expand the possibilities, he considered the serial developments of the functions and followed them to get a new series of integrated topics (without paying attention to convergence problems, of course).
The expansion of (1 + x) m, when m is total, although called Newton's binomial, is really interesting when m is incomplete, then polynomial is not an infinite series. m in the middle of two integers (1/2, 3/2, ...) is already due to Newton the answer of the case, since it showed that the same rule is applied as the coefficients of polynomials for the coefficients.
In order to rely on what was being done, Newton will refer to the relationships of the increments: flow " the first relationship of emerging increments " or " the last relationship of fungible increments ". In view of the image, suppose we advance a little the abscisa, then the surface increases and we have to get a relationship between the increments of surface and abscisa, but the first relationship flows is ", before beginning to move ... Likewise, considering the process backwards, the increments disappear and the last relation of destructive increments " is the flow. The idea of indeterminate limit can be raised.
We must share the honors
Among Newton's works, those related to Calculus are: "De Analysi per Aequationes Numero Terminorum Infinitas" (written around 1669, published in 1711), "Methodus Fluxionum et Serierum Infinitorum" (written in 1671, published in 1736), "Tractatus de Quadratura Curvarum" (written in 1693, pages 1704) and "principi" (pp. As can be seen, twenty years passed between the obtaining of the rescued and their dismissal, and thus, in 1675, Leibniz came on his part to similarities. Leibniz's first article was published in 1684, anticipating for three years "Principia".
In 1698 Fatio de Duillier, a friend of Newton, published a book in which he recognized all merit by denouncing that Leibniz had made plagiarism. Leibniz defended himself and spent ten years until the second attack came in an article by Keill. This article appeared in the journal of the Royal Society and Leibniz, as an associate, requested in 1711 the secretary to clarify the problem.
When the president was Newton, a committee was appointed and the commission's decision was even tougher for Leibniz. In addition, they decided to publish the collection of letters "Commercium Epistolicum" against Leibniz. The debate grew and some people of Leibniz realized some errors of Newton. Leibniz, in 1714, wrote the program " History et origo Calculi differentialis " to tell his truth. Despite his death two years later, Newton continued to attack.
XX. Until the nineteenth century this point has been undecided, but when the manuscripts of Leibniz have been analysed, their merit has been definitively recognized and today both have the honor of being creators of Calculus. The debate, however, affected England more, where local and mainland mathematicians moved away and the development of the Calculus occurred almost entirely on the line of Leibniz.
New paths and solid bases
The diffusion of the calculus was very agile thanks to the magazines of recent creation. Only in the magazine "Acta Eruditorum" there are more than a hundred articles in Leibniz from the first to the next twenty-five years, most written by Leibniz himself and the Bernouilli brothers. XVIII. In the eighteenth century the Calculus would reach the top with numerous methods and applications, in which the name of Euler should be placed far above his contemporaries. Next to it stand out the second generation of bernouillitos, D'Alembert and, later, Lagrange.
But the Calculus had an original sin and the English bishop Berkeley denounced it harshly in 1735, in his book "The Analyst": the last relations of Newton's devastating quantities mentioned at the basis of reasoning " and the "infinitesimals" of Leibniz were unacceptable by the queen. In the words of Berkeley: "What can gullible the second or third flow and the second or third differential should not concern, in my opinion, the problems of the Divinity", that is, one and the other are matters of faith. Yes, it does not question the results obtained.
Although one hundred years earlier Cavalieri had written "error is a problem of philosophers and not of mathematicians", mathematicians who tried to build Calculus on solid bases, it is remarkable the importance given by D'Alembert to the concept of limit for the "Encyclopedie". XIX. At the beginning of the twentieth century Bolzano, Prague and Cauchy gave an adequate definition of the limit in Paris (equivalent to that which exists in any book today) and from it the derivative is defined.
The integral, with Cauchy, went from being the inverse of the derivative to defining it by a limit and then had to prove the inverse between them. The Integral followed its own path and created the so-called Theory of Measure; Lebesgue XX. What ended at the beginning of the twentieth century. In addition to the general definition of the integral, he achieved the differentiation theorem, the modern formulation of Newton-Leibniz theorem.





