Poliminos (II)
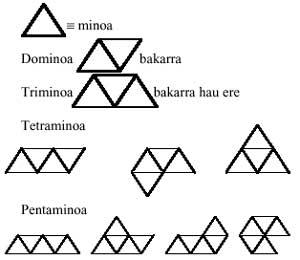
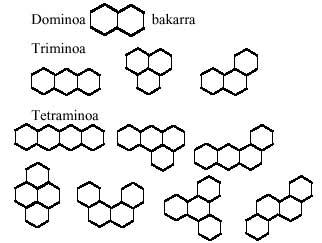
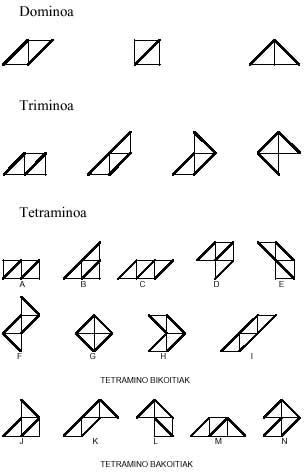
In the previous issue we talk about polymines. From the word “domino” we get the words trimino, tetramino, pentamino, hexamino and, in general, polimino. In it we obtained the polyminus games identifying two mino, such as trimino>three mino, tetramino -four mino, pentamino -five mino and hexamino -six minos. In all of them we accept the mino equivalence?
In this issue we will expand the concept of “mino” and, in addition to the picture, we will give you meanings of equilateral triangle and hexagon. The reason is that the only regular polygon that can form the plane is that of the three mentioned, the square, the equilateral triangle and the hexagon.
Starting with the equilateral triangles and following the same development, we will form triangular games of domains, triminos, tetraminos, pentaminos and hexaminos. All the pieces of these games are:
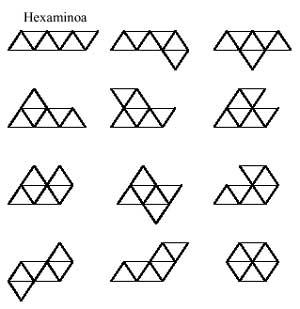
A question comes to mind: can pentamines be formed with medes and triminuses? And then another: and can hexaminos be formed with two triminos?. And another: can hexaminos be formed with dominos and tetraminos?. The answer to the first is yes. But that of others does not. What are the examines that cannot form two triminuses? and those who cannot be formed by the union of domains and tetraminos?
Tetraminos offer us another alternative, that is, can you say that tetraminos are smooth tetrahedron developments?. Or in other words, can tetrahedron be completed with tetraminos?
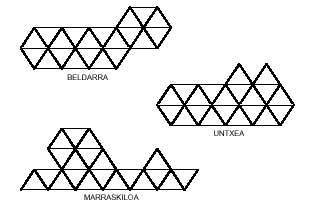
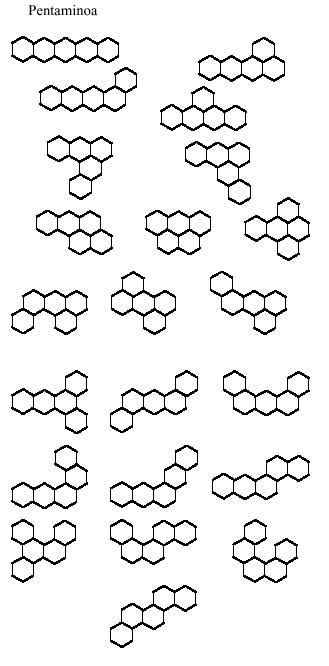
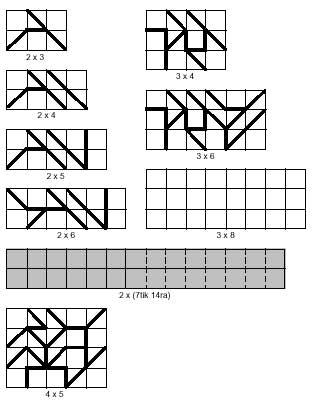
Below are three images that may be made up of triangular pentamines:
The answer is for you to try to complete twelve hexaminos.
We leave the triangular polymers with the latter.
Before moving forward, of course, the easiest way to answer the questions posed here is through the elaboration of polymines, which we recommend.
Now let's move on to hexagonal polymers.
Hexagonal polymers, as it could not be otherwise, consist of hexagons, which is what we are going to do now, taking at least the hexagon:
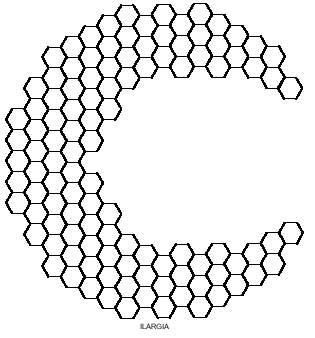
The hexagonal ones are not brought since there are 82 different hexamines. The truth is that the number of pentamines (22) is quite large to play with them. However, below we propose some images.
To complete with hexagonal tetramines we propose the following images (see image attached), but one of the eight cannot be completed.
You have to look for it. In all of them seven tetraminos will be necessary.
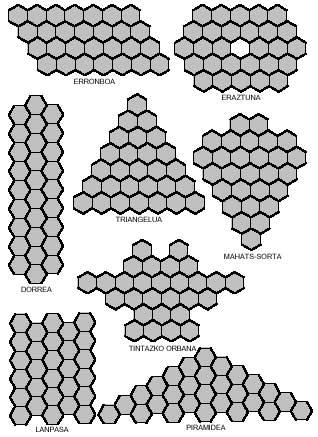
You can also obtain curious images with hexagonal pentamines such as those of the following figure. Four of them, as you can see, can be divided into two parts, and in both, in the rhombus and in the corridor, placing the two parts differently, longer rhombuses and lanps can be achieved.
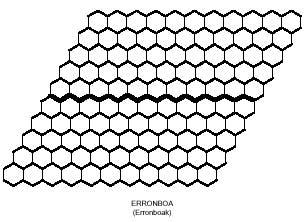
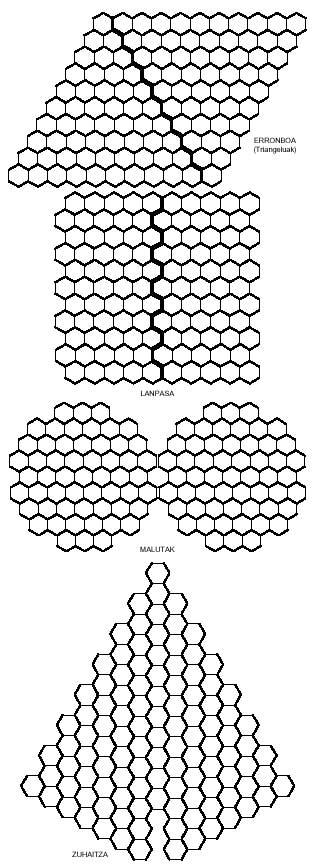
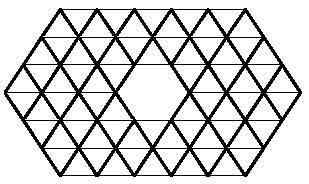
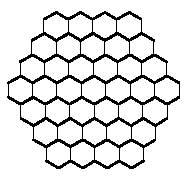
Just as we tried to form rectangles with square polymers, with hexagonal polymers we could try to build hexagons. Hexagons formed by hexagons need 1, 7, 19, 37, 61, 91, 127,… hexagons. These amounts are not reached by the triminos (9), nor by the tetraminos (28) nor by the pentamines (110). But if you notice, the union of triminus and tetramine allows to form a hexagon of 37 hexagons. But can this hexagon really be completed with three triminuses and seven tetramines? Here's another question for you to try to answer, along with the 37-hexagon hexagon:
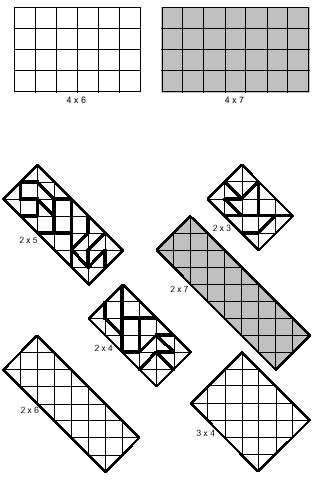
So far we have built polymines with regular polygons, but this is not the only possibility. We bring you another, formed by isosceles straight triangles:

Since in this case hypotenuse and catetuses are different, hypotenuses are associated with hypotenus and catettos with catettos. This is why there is more than one domino. Note that this triangle has lost the symmetry of regular polygons.
The pieces created with this mino are:
We leave it here for now. Let's just say two things: There are 30 pentamines and 107 hexamines.
If the surface of each triangle is a, the surface of all domains will be 6 and a surface box 6 cannot be formed. The surface of the triminos is 12 and cannot be formed square. Another is the case with tetraminos, with a total surface area of 56. However, there are squares that can be part of the subset of the complete tetramine system. Just look at the image below.

As you can see in the following image, the pictures are of two types: one with the part of the picture formed by hypotenus and the other with the chained part.
In addition to the squares you can build rectangles, among which you can also distinguish the two previous types. In the image below you can see the rectangles of both types. In both cases there are examples of rectangles formed by several pieces. Grey rectangles should be formed with 14 tetramins, which is not possible. This statement is not free, as disability is demonstrated. The classification of tetramins is related to this demonstration.
Tetraminos pairs have an even number of hypotenuses in the outer boundary and in both directions. On the contrary, odd tetramines have an odd number in both directions. The demonstration is based precisely on the fact that to complete the rectangle it is necessary that in both directions there be a couple of hypotheses. However, there are five odd tetramines, so this cannot be filled if you want to catch the 14 tetraminos.
The white rectangles that appear in the image are for you to try to solve them.
For the brave we have a difficult job. By discarding symmetrical tetramins, could the surface table 16a be formed other 8 tetraminos (C,E,F,I,J,K,L,N)? (the side of this box would be formed by 4 chained). And the second question, considering the symmetrical 8 non-symmetrical tetramines (i.e. 16 tetramines in total), but now they cannot be turned around, could the favorable picture of 4 hypotenus be completed?





