Poliminoak (II)
Aurreko alean poliminoez mintzatu ginen. “Domino” hitzetik trimino, tetramino, pentamino, hexamino eta orokorrean polimino hitzak atera genituen. Bertan do-mino þ bi mino identifikatuz lortzen genituen polimino-jokoak, hala nola trimino þ hiru mino, tetramino þ lau mino, pentamino þ bost mino eta hexamino þ sei mino. Guztietan mino þ lauki baliokidetza onartzen genuen.
Ale honetan “mino” kontzeptua zabaldu egingo dugu eta laukiaz aparte triangelu aldekide eta hexagono esanahiak ere emango dizkiogu. Honen arrazoia ondokoa da: planoa osa dezaketen poligono erregular bakarrak aipatutako hiruak, hots, laukia, triangelu aldekidea eta hexagonoa, izatea.
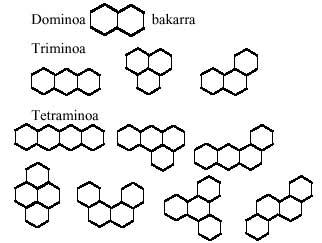
Triangelu aldekideekin hasiz eta garapen berberari jarraituz, domino, trimino, tetramino, pentamino eta hexaminoen joko triangeluarrak osatuko ditugu. Hona hemen, joko hauen pieza guztiak:
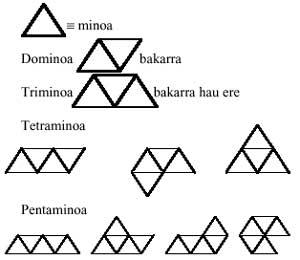
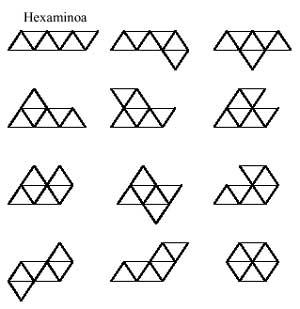
Galdera bat datorkigu burura: osa al daitezke pentaminoak domino eta triminoz?. Eta ondoren beste bat: eta osa al daitezke hexaminoak bi triminoz?. Eta beste bat: osa al daitezke hexaminoak domino eta tetraminoen bidez?. Lehenengoaren erantzuna baiezkoa da. Besteena, ordea, ezezkoa. Zeintzuk dira bi triminoz osa ezin diren hexaminoak?; eta domino eta tetraminoak elkartuz osa ezin daitezkeenak?
Tetraminoek beste aukera bat ematen digute, hau da, esan al daiteke tetraminoak tetraedroaren garapen launak direla?. Edo bestela esanda, tetraminoekin osa al daiteke tetraedroa?
Hona hemen pentamino triangeluarrez osa daitezkeen hiru irudi:
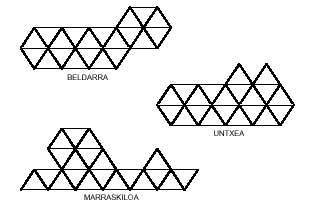
Horra hor erantzuna, hamabi hexaminoez osatzen saia zaitezen.
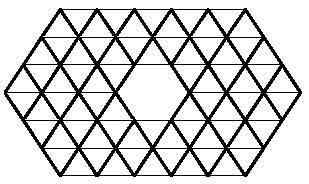
Polimino triangeluarrak azken honekin utziko ditugu.
Aurrera segitu baino lehen, zer esanik ez, hemen plazaratutako galderei erantzuteko erarik errazena poliminoak egitea da, eta horixe gomendatzen dizugu.
Pasa gaitezen orain polimino hexagonaletara.
Polimino hexagonalak, nola ez, hexagonoz osatzen dira, eta horixe egingo dugu orain hemen, mino bezala hexagonoa harturik:
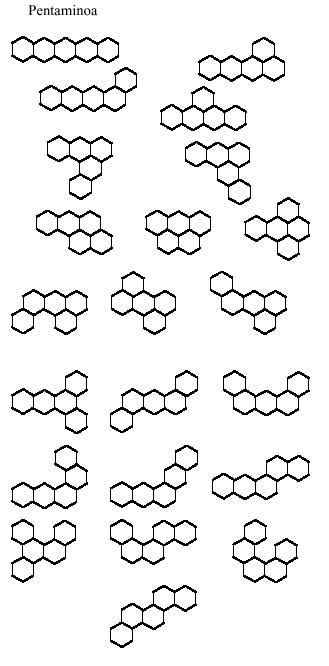
Hexamino hexagonalak ez ditugu hona ekarriko, 82 hexamino ezberdin badago eta. Egia esan jadanik pentaminoen kopurua (22) handi samarra geratzen da beroriekin jolasteko. Hala ere, zenbait irudi proposatuko dizugu aurrerago.
Tetramino hexagonalez osatzeko ondorengo irudiak proposatzen dizkizugu (ikus ondoko irudia), baina zortzi irudietako bat ezin da osatu.
Hori zein den zeuk bilatu beharko duzu. Guztietan zazpi tetraminoak erabili beharko dira.
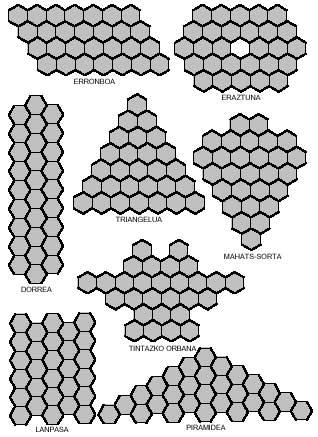
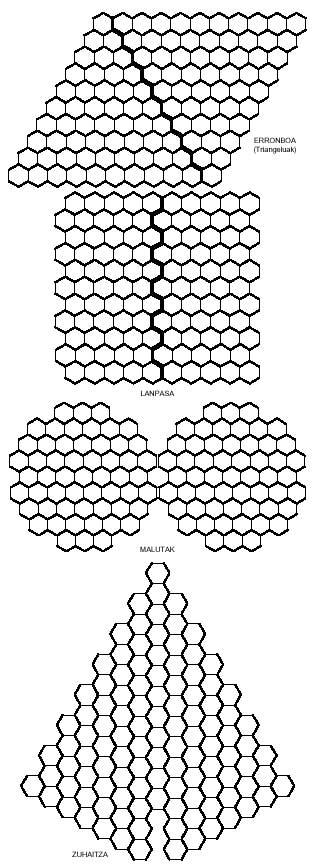
Pentamino hexagonalez ere lor daitezke irudi bitxiak; hurrengo irudikoak bezalakoak esate baterako. Hauetako lau, ikusten den bezala, bi zatitan bereiz daitezke eta bietan, erronboan eta lanpasean, bi zatiak beste era batzuetara kokatuz erronbo eta lanpas luzeagoak lor daitezke.
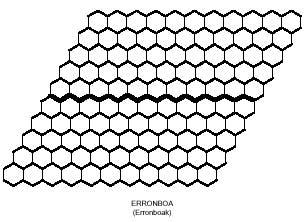
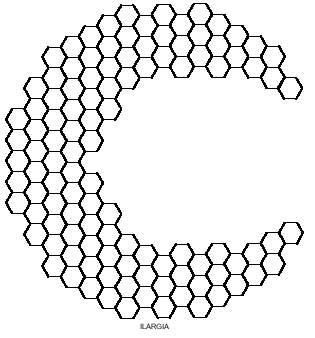
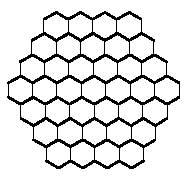
Polimino karratuekin laukizuzenak osatzen saiatzen ginen bezala, polimino hexagonalekin hexagonoak eraikitzen saia gintezke. Hexagonoz osatutako hexagonoek 1, 7, 19, 37, 61, 91, 127,… hexagono behar dute. Kopuru horiek ez dituzte lortzen ez triminoek (9), eta ez tetraminoek (28) eta ezta pentaminoek (110) ere. Baina ohartzen bazarete, triminoa eta tetraminoa elkartuz 37 hexagonoko hexagonoa osatzerik badago. Baina benetan osa al daiteke esandako hexagonoa hiru trimino eta zazpi tetraminoez? Hor daukazu beste galdera bat erantzuten saia zaitezen, eta ondoan 37 hexagonotako hexagonoa ere bai:
Orain arte poliminoak poligono erregularrez eraiki ditugu, baina ez da hau dagoen posibilitate bakarra. Beste bat ekarriko dizugu hona; triangelu zuzen isoszelez osatutakoa hain zuzen ere:

Kasu honetan hipotenusa eta katetuak ezberdinak direnez, hipotenusak hipotenusekin eta katetuak katetuekin elkartuko ditugu. Hau da, hain zuzen, domino bat baino gehiago egoteko arrazoia. Kontura zaitez triangelu honek poligono erregularren simetria galdu duela.
Hona hemen mino honekin sortzen diren pieza ezberdinak:
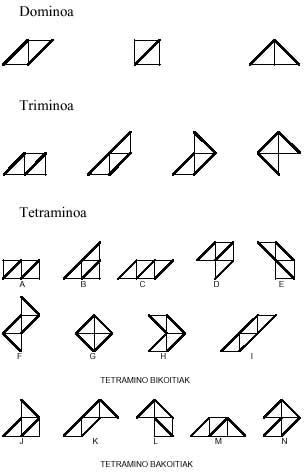
Hemen utziko dugu oraingoz. Bi gauza besterik ez dugu esango: 30 pentamino eta 107 hexamino daudela.
Triangelu bakoitzaren azalera a bada, domino guztien azalera 6a izango da eta ezin da 6a azalerako laukirik osatu. Triminoen azalera 12a-koa da eta ezin da laukirik eratu. Tetraminoekin beste horrenbeste gertatzen da, azalera osoa 56a-koa delarik. Hala ere tetraminoen sistema osoaren azpimultzoz osa daitezkeen laukirik badago. Horretarako hurrengo irudiari begiratzea baino ez diozu egin behar.

Irudi honetan ikus dezakezunez, laukiak bi motatakoak dira: bata laukiaren aldea hipotenusaz osatua duena eta bestea katetuz osatua duena.
Laukiez aparte laukizuzenak ere eraiki daitezke, hauen artean ere aurreko bi motak bereiz daitezkeelarik. Ondoko irudian bi motetako laukizuzenak ikus daitezke. Bi kasuetan zenbait piezaz osatutako laukizuzenak daude adibide gisa. Laukizuzen grisak 14 tetraminoz osatu beharko lirateke, baina hori ezinezkoa gertatzen da. Baieztapen hau ez da debaldekoa; ezintasuna frogaturik bait dago. Frogapen honekin zerikusirik badauka tetraminoen sailkapenak.
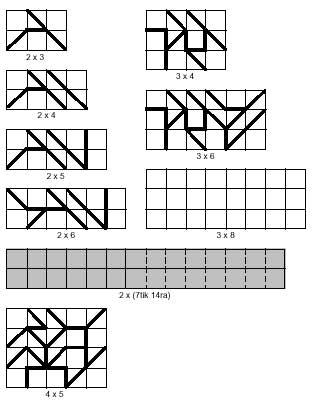
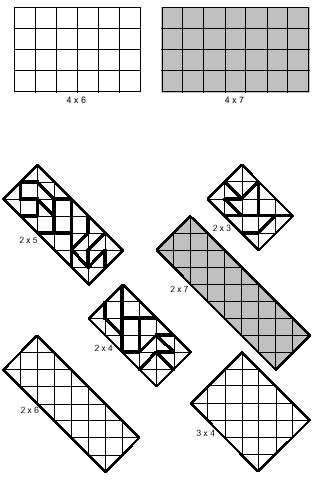
Tetramino bikoitiek kanpoko mugan eta bi norantzetan hipotenusa-kopuru bikoitia daukate. Tetramino bakoitiek, aldiz, kopuru bakoitia dute bi norantzetan. Honetan oinarritzen da hain zuzen ere frogapena: laukizuzena osatu ahal izateko bi norantzetan hipotenusa-kopuru bikoitiak egon behar du. Hala ere bost tetramino bakoiti daudenez, hau ezin da bete 14 tetraminoak hartu nahi badira.
Irudian azaltzen diren laukizuzen zuriak, zeu ebazten saia zaitezen dira.
Adoretsuentzat lan zaila daukagu. Tetramino simetrikoak baztertuz, beste 8 tetraminoz (C,E,F,I,J,K,L,N) 16a azalerako laukia osa al liteke? (lauki honen aldea 4 katetuz legoke osaturik). Eta bigarren galdera, 8 tetramino ez-simetrikoen simetrikoak kontutan hartuz (hau da guztira 16 tetramino), baina orain ezin zaie buelta eman, 4 hipotenusako aldeko laukia osa al liteke?






