Poliminos (II)
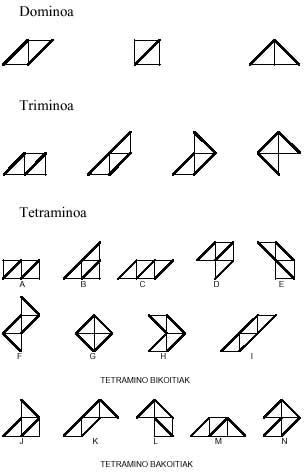
En el número anterior parlem dels poliminos. De la paraula “domino” traiem les paraules trimino, tetramino, pentamino, hexamino i, en general, polimino. En ella obteníem els jocs de polimino identificant dos mino, com ara trimino>tres mino, tetramino -quatre mino, pentamino -cinc mino i hexamino -sis minos. En tots ells acceptem l'equivalència mino?
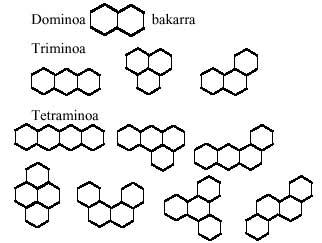
En aquest número ampliarem el concepte de “mino” i, a més del quadre, li donarem significats de triangle equilàter i hexàgon. La raó és que l'únic polígon regular que pot formar el pla sigui el dels tres esmentats, el quadrat, el triangle equilàter i l'hexàgon.
Començant amb els triangles equilàters i seguint el mateix desenvolupament, formarem jocs triangulars de dominis, triminos, tetraminos, pentaminos i hexaminos. Totes les peces d'aquests jocs són:
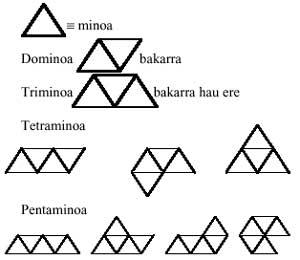
Ens ve al capdavant una pregunta: es poden formar pentaminos amb medos i triminos? I després altra: i es poden formar hexaminos amb dos triminos?. I un altre: es poden formar hexaminos amb dominos i tetraminos?. La resposta a la primera és afirmativa. Però el dels altres no. Quins són els examinos que no poden formar dos triminos? i els que no poden formar-se mitjançant la unió de dominis i tetraminos?
Els tetraminos ens ofereixen una altra alternativa, és a dir, es pot dir que els tetraminos són desenvolupaments llisos del tetraedre?. O dit d'una altra manera, es pot completar el tetraedre amb tetraminos?
A continuació es presenten tres imatges que poden estar formades per pentaminos triangulars:
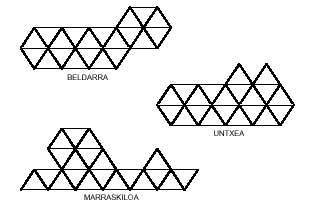
La resposta és perquè intentis completar dotze hexaminos.
Deixem els polímers triangulars amb aquest últim.
Abans de seguir endavant, per descomptat, la forma més senzilla de respondre a les preguntes aquí plantejades és a través de l'elaboració de poliminos, que et recomanem.
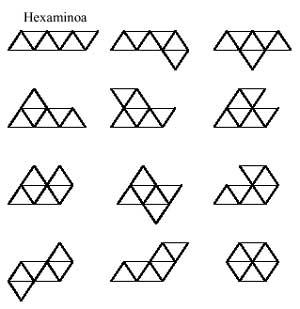
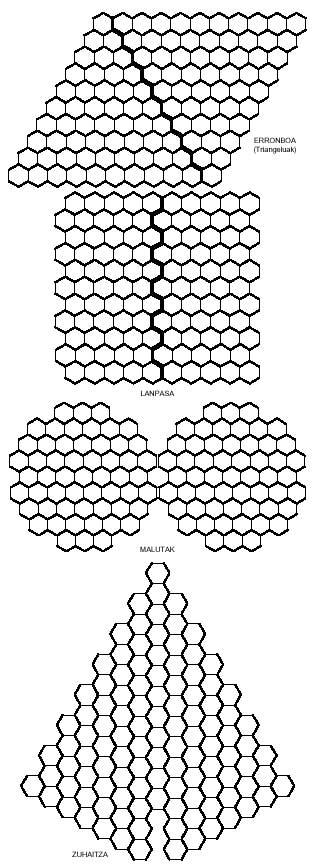
Passem ara als polímers hexagonals.
Els polímers hexagonals, com no podia ser d'una altra manera, es componen d'hexàgons, que és el que farem ara, prenent com a mínim l'hexàgon:
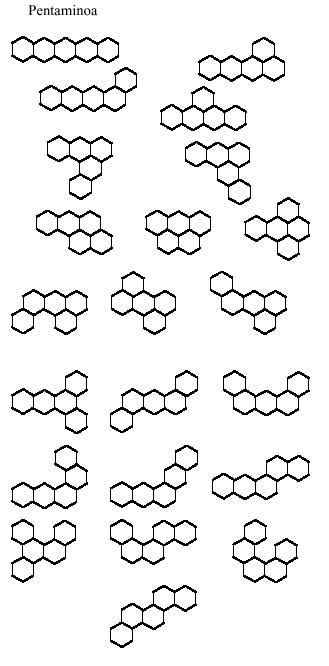
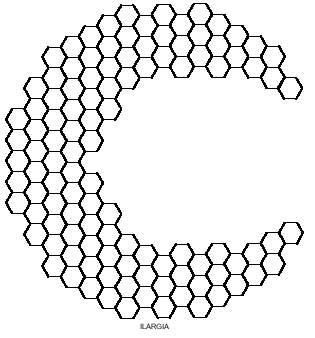
Els hexagonals no es porten ja que hi ha 82 hexaminos diferents. La veritat és que el número de pentaminos (22) queda bastant gran per a jugar amb ells. No obstant això, més endavant et proposem algunes imatges.
Per a completar amb tetraminos hexagonals et proposem les següents imatges (veure imatge adjunta), però una de les vuit no es pot completar.
Has de buscar-ho tu. En tots ells seran necessaris set tetraminos.
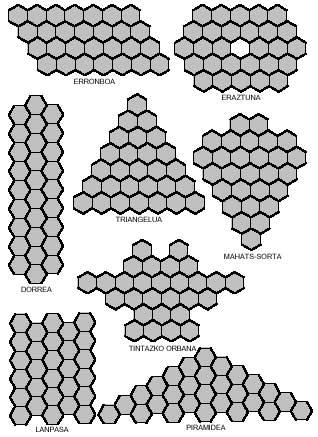
També es poden obtenir imatges curioses amb pentaminos hexagonals com els de la següent figura. Quatre d'elles, com es veu, es poden dividir en dues parts, i en ambdues, en el rombe i en el passadís, col·locant les dues parts d'una altra manera, es poden aconseguir rombes i lanpas més llargs.
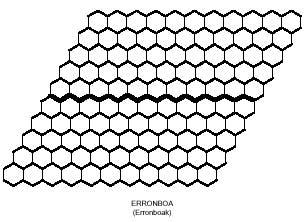
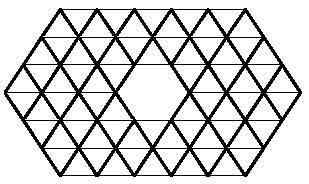
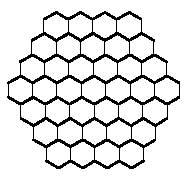
Igual que tractàvem de formar rectangles amb polímers quadrats, amb els polímers hexagonals podríem intentar construir hexàgons. Els hexàgons formats per hexàgons necessiten 1, 7, 19, 37, 61, 91, 127,… hexàgons. Aquestes quantitats no són aconseguides pels triminos (9), ni pels tetraminos (28) ni pels pentaminos (110). Però si us adoneu, la unió de trimino i tetramino permet formar un hexàgon de 37 hexàgons. Però realment es pot completar aquest hexàgon amb tres triminos i set tetraminos? Aquí tens una altra pregunta perquè intentis contestar, juntament amb l'hexàgon de 37 hexàgons:
Fins ara hem construït poliminos amb polígons regulars, però no és aquesta l'única possibilitat. Et portem un altre, format per triangles rectilinis isòsceles:

Atès que en aquest cas la hipotenusa i els catets són diferents, les hipotenuses s'associen amb hipotenus i els catets amb catets. Aquesta és la raó per la qual hi ha més d'un dominó. Noti's que aquest triangle ha perdut la simetria dels polígons regulars.
Les peces que es creen amb aquest mino són:
Ho deixem aquí de moment. Només direm dues coses: Hi ha 30 pentaminos i 107 hexaminos.
Si la superfície de cada triangle és a, la superfície de tots els dominis serà 6 i no es podrà formar un quadre de superfície 6. La superfície dels triminos és de 12 i no es pot formar quadrada. Un altre punt ocorre amb els tetraminos, amb una superfície total de 56. No obstant això, existeixen quadrats que poden formar part del subconjunt del sistema de tetraminas complet. Per a això només has de mirar la següent imatge.

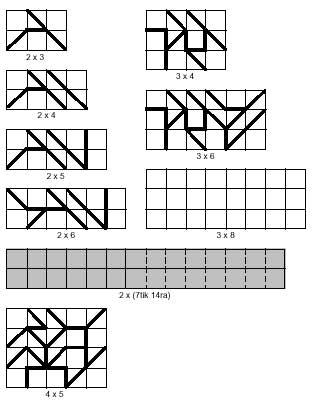
Com pots veure en la següent imatge, els quadres són de dos tipus: un amb la part del quadre formada per hipotenus i l'altre amb la part encadenada.
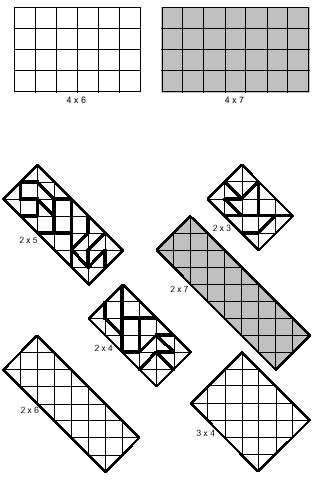
A més dels quadrats es poden construir rectangles, entre els quals també es poden distingir els dos tipus anteriors. En la imatge següent es poden veure els rectangles de tots dos tipus. En tots dos casos hi ha exemples de rectangles formats per diverses peces. Els rectangles grisos haurien de formar-se amb 14 tetraminas, la qual cosa no és possible. Aquesta afirmació no és gratuïta, ja que la incapacitat està demostrada. La classificació dels tetraminas està relacionada amb aquesta demostració.
Els tetraminos parells presenten un nombre parell d'hipotenuses en el límit exterior i en totes dues direccions. Per contra, els tetraminos imparells tenen un nombre imparell en totes dues direccions. La demostració es basa precisament en el fet que per a completar el rectangle és necessari que en totes dues direccions hi hagi un nombre parell d'hipòtesi. No obstant això, hi ha cinc tetraminos imparells, per la qual cosa això no es pot omplir si es volen agafar els 14 tetraminos.
Els rectangles blancs que apareixen en la imatge són perquè intentis resoldre'ls.
Per als valents tenim un treball difícil. Descartant els tetraminos simètrics, podria formar-se el quadre de superfície 16a altres 8 tetraminos (C,E,F,I,J,K,L,N)? (el costat d'aquesta casella estaria format per 4 encadenats). I la segona pregunta, tenint en compte les simètriques de 8 tetraminos no simètrics (és a dir, 16 tetraminos en total), però ara no se'ls pot donar la volta, es podria completar el quadre favorable de 4 hipotenus?





