Onde estou? cálculo de latitude e lonxitude
Esperteime asustado. A luz intensa doíame os ollos e impedíame ver a contorna. Aos poucos empecei a descubrir onde estaba: nunha illa arenosa con só dúas palmeiras. O último que me acordaba era o que saín da escola e cos meus amigos fun a casa. Alí estaba a miña mochila escolar, naquel radiante escenario, xunto a una botella semienterrada na area. Coma se fose protagonista dun cómic, en lugar de preguntarme como cheguei a min mesmo, sentín a necesidade de saber onde estaba. Tiña claro os pasos que tiña que dar: saber a localización, escribir nun papel, meter a mensaxe de axuda na botella, tiralo ao mar e esperar. Sen ter en conta que a situación era totalmente absurda, empecei a traballar.
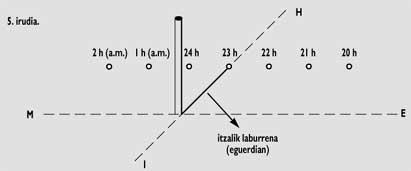
No meu reloxo eran as 22 e vin que o Sol subía cara á esquerda no horizonte. Como era posible?
Paira un comezo máis sustentable do curso, acordeime de que o profesor de Ciencias Naturais deunos os apuntamentos de Astronomía. Púxenme cara á mochila sen perder tempo. Estudei a primeira imaxe destes apuntamentos e as explicacións que alí escribín:
“Cando miramos ao Sol, observaremos que se está desprazando polo leste (pola esquerda) cara ao oeste (cara á dereita), mentres que o mediodía indica o sur. O movemento é o mesmo paira o resto de estrelas, planetas e mesmo a Lúa. O observado é consecuencia do movemento da Terra ao redor do seu eixo en dirección oposta, é dicir, de oeste a leste."
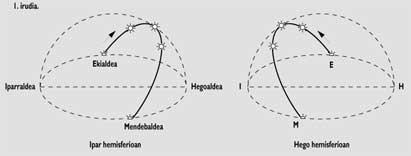
Con todo, eu vin un movemento inverso que me indicaba que o Sol estaba a observar “patas para arriba”. Noutras palabras, miraba desde o hemisferio sur. De feito, neste hemisferio, o Sol representa ao norte ao mediodía e, por tanto, mesturei este e oeste na miña primeira observación. Sen dúbida, estaba no hemisferio sur!
Tras obter o primeiro dato da miña localización, seguín analizando os apuntamentos:
“A latitude nun punto P por encima da Terra é o ángulo que forma a vertical deste punto co plano do ecuador (Figura 2). Por tanto, a latitude do Polo norte é de 90º, a do País Vasco 42º-43º e a do Ecuador 0º”.
“Una forma de calcular a latitude: no equinoccio de outono (23 de setembro) e no de primavera (21 de marzo), os raios solares atacan perpendicularmente no Ecuador (é dicir, ao mediodía non producen sombra). Como son paralelos entre si, se medimos a sombra provocada polos raios solares en calquera outra posición, poderiamos calcular a nosa latitude” (Figura 3).
“O obxecto PA xerará sombra de PB cando estea en posición vertical no punto P, é dicir, cando o Sol atópese no punto máis alto do horizonte (é dicir, ao mediodía). Mediante o obxecto e as lonxitudes da sombra, calcularemos o ángulo b. Os ángulos b e ? (latitude) son iguais por razóns trigonométricas.
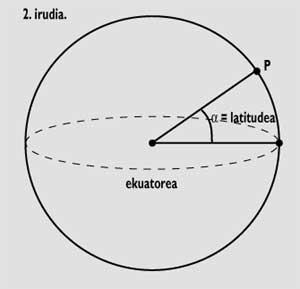
tg < = lonxitude sombra / lonxitude obxecto”
“Empecemos a traballar”, pensei entre min. Collín un bolígrafo e cravei a area nun lugar moi suave. “Mágoa que non haxa obxectos máis longos paira poder cometer menos erros. No entanto, hoxe 20 de setembro, faltan 3 días paira o equinoccio de outono. Cun pouco de sorte, os dous erros equilibraranse”.
Cada minuto comecei a marcar os lugares onde chegaba a sombra e obtiven o seguinte resultado (figura 4):
A sombra máis pequena (mediodía) produciuse ás 23 do meu reloxo. Vin claro que estaba moi lonxe de Euskal Herria. Deixando paira despois a análise deste dato, centreime no cálculo da latitude.
Lonxitude da sombra = 5,6 cm; do
bolígrafo = 13 cm.
Por tanto,
tg < = 5,6/13=0,43 e (menos mal que tiña calculadora na mochila!)
b = latitude = 23º 18’.
Estaba xunto ao trópico de Capricornio! (3).
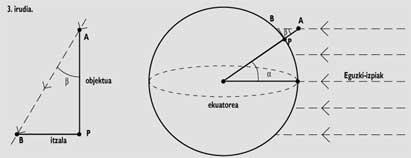
“A lonxitude nun punto P por encima da Terra é o ángulo que forma o meridiano deste punto co meridiano de Greenwich (Figura 5). Aos sitios situados ao oeste do meridiano de Greenwich engádese W (West, abreviatura do oeste inglés) e aos situados ao leste E (East, do leste)”.
“Una forma de calcular a lonxitude: Si en calquera lugar de Euskal Herria medimos e marcamos as sombras que produce un obxecto vertical ao longo do día, veremos que a sombra máis curta do inverno prodúcese ás 13 horas e minutos. Este fenómeno prodúcese ás 14 horas e minutos no verán, debido ao avance da hora oficial respecto da hora solar, que é dunha hora e 2 horas respectivamente. Tendo en conta que o meridiano de Greenwich pasa por Tarbe e Huesca, entre outras cousas, paira cando o Sol chega a Euskal Herria ten un pequeno "atraso": 3-4 minutos en Zuberoa e 10 13 minutos en Bizkaia.
Paira calcular a lonxitude dun lugar situado ao oeste do meridiano de Greenwich, deberemos tomar a hora correspondente á sombra mínima e calcular o seu atraso respecto ao mediodía (en caso de estar ao leste deberiamos medir o progreso).”
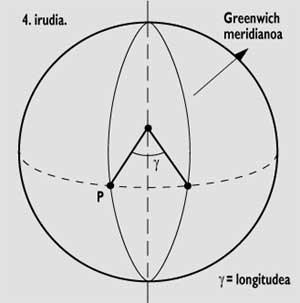
“Como o Sol vira todo o día (360º):
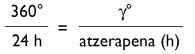
ou en minutos:

sendo gº a lonxitude”.
Baseeime nas explicacións dos apuntamentos paira facer os meus cálculos. Na illa o mediodía produciuse ás 23 segundo o meu reloxo. Isto indicaba a hora oficial do verán, polo que debía quitar dúas horas. Así, o mediodía produciuse ás 21 horas. Noutras palabras, tiña 9 horas de atraso respecto ao meridiano de Greenwich. Por tanto:
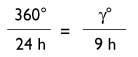
e desde aquí
gº = 135° W (Oeste)
Volvín abrir a mochila, saín o atlas e comecei a frenética procura da miña posición. Nesa posición atopei as illas Gambier da Polinesia francesa, próximas a Mururo. A poucos quilómetros dese atolón que quizá se fixo tan famoso.
Sen perder tempo, escribín as coordenadas (23º 18’ S; 125º W) coa mensaxe de axuda que lle correspondía nun papel, metinas na botella e tireinas ao mar con moita forza.
As primeiras estrelas empezaban a saír, a maioría descoñecidas paira min: alí sería Alpha Centauri, a estrela máis próxima ao Sol, a Nube Maior e Pequena de Magallanes, e as galaxias máis próximas a nós... De súpeto, é dicir, xordos, profundos e terribles. Asustado, abrinme os ollos e deime conta de que estaba na miña habitación. Nunca souben o porqué deste aparente pesadelo.