Como converter o rectángulo en cadrado?
O camiño a seguir paira atopar a resposta divídese en varias etapas.
- Ao pé do rectángulo: si chamamos a e á altura o valor da superficie b virá dado pola fórmula axb. Entón, o valor a outorgar a cada lado paira formar un cadrado con esa superficie será a.b.
- Por tanto, pasamos do problema que tiñamos antes a un novo problema. Si coñécense os valores a e b, como completar o valor a.b.
Imos tentalo.
Na figura 1:
OA=1 unidade AB = valor a (con compás) OA'=b (con compás) A'B'= x AB e A'B' son perpendiculares á liña OM
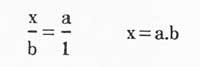
A continuación:
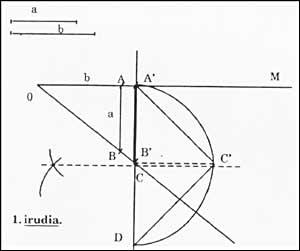
B'D = unidade C, punto medio do segmento A'D con centro A'C'D en C B'C', perpendicular á liña A'D' desde B'C', sendo a altura do triángulo recto A'C'D = B'C' A'B'
B'C'= a.b
Ese era o valor que estabamos a buscar.
Basta, por tanto, repetir o traballo que realizamos paira converter un rectángulo en cadrado, substituíndo aos xenerais a e b polo pé e as alturas concretas de devandito rectángulo. A continuación, utilizando o segmento B'C' como lado, paira completar o cadrado.
Esta evolución é interesante en si mesma, pero o máis interesante é o fácil que resulta si pensamos en rectificar outros polígonos. Así, o rectángulo cumpre a función de mediador.
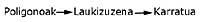
Cadrar un polígono, é dicir, convertelo nun cadrado equivalente á superficie, non é fácil si queremos facelo dunha maneira correcta, pero se utilizamos o rectángulo como elemento auxiliar intermedio todo é máis sinxelo.
Como o cadrar un polígono e calcular a súa superficie son equivalentes, o interese desta operación parece evidente.
Neste número, cambiando un pouco de tema, queremos propor un novo xogo.
A e B son vagóns dun tren. L, a locomotora. T é un túnel. Ao longo deste túnel pódese chegar a un locomotora pero sen coches.
A dobre liña que aparece na figura 2 é a vía férrea.
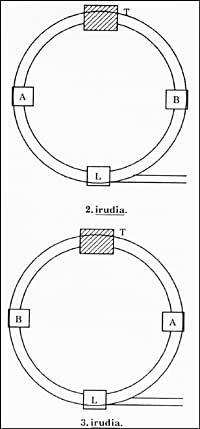
A esencia do xogo é como pasar da situación que aparece na figura 2 á que aparece na figura 3 movéndose o menos posible a locomotora?





