¿Cómo convertir el rectángulo en cuadrado?
El camino a seguir para encontrar la respuesta se divide en varias etapas.
- Al pie del rectángulo: si llamamos a y a la altura el valor de la superficie b vendrá dado por la fórmula axb. Entonces, el valor a otorgar a cada lado para formar un cuadrado con esa superficie será a.b.
- Por tanto, hemos pasado del problema que teníamos antes a un nuevo problema. Si se conocen los valores a y b, cómo completar el valor a.b.
Vamos a intentarlo.
En la figura 1:
OA=1 unidad AB = valor a (con compás) OA'=b (con compás) A'B'= x AB y A'B' son perpendiculares a la línea OM
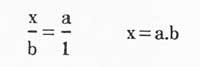
A continuación:
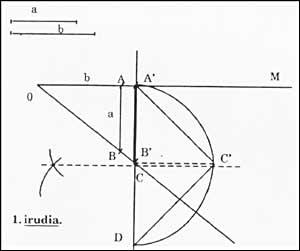
B'D = unidad C, punto medio del segmento A'D con centro A'C'D en C B'C', perpendicular a la línea A'D' desde B'C', siendo la altura del triángulo recto A'C'D = B'C' A'B'
B'C'= a.b
Ese era el valor que estábamos buscando.
Basta, por tanto, repetir el trabajo que hemos realizado para convertir un rectángulo en cuadrado, sustituyendo a los generales a y b por el pie y las alturas concretas de dicho rectángulo. A continuación, utilizando el segmento B'C' como lado, para completar el cuadrado.
Esta evolución es interesante en sí misma, pero lo más interesante es lo fácil que resulta si pensamos en rectificar otros polígonos. Así, el rectángulo cumple la función de mediador.
Cuadrar un polígono, es decir, convertirlo en un cuadrado equivalente a la superficie, no es fácil si queremos hacerlo de una manera correcta, pero si utilizamos el rectángulo como elemento auxiliar intermedio todo es más sencillo.
Como el cuadrar un polígono y calcular su superficie son equivalentes, el interés de esta operación parece evidente.
En este número, cambiando un poco de tema, queremos proponer un nuevo juego.
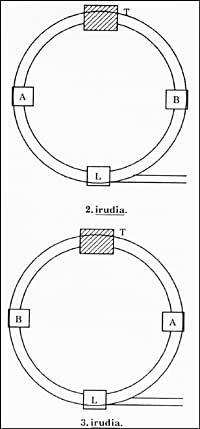
A y B son vagones de un tren. L, la locomotora. T es un túnel. A lo largo de este túnel se puede llegar a una locomotora pero sin coches.
La doble línea que aparece en la figura 2 es la vía férrea.
La esencia del juego es cómo pasar de la situación que aparece en la figura 2 a la que aparece en la figura 3 moviéndose lo menos posible la locomotora?





