Com convertir el rectangle en quadrat?
El camí a seguir per a trobar la resposta es divideix en diverses etapes.
- Al peu del rectangle: si cridem a i a l'altura el valor de la superfície b vindrà dau per la fórmula axb. Llavors, el valor a atorgar a cada costat per a formar un quadrat amb aquesta superfície serà a.b.
- Per tant, hem passat del problema que teníem abans a un nou problema. Si es coneixen els valors a i b, com completar el valor a.b.
Ho intentarem.
En la figura 1:
OA=1 unitat AB = valor a (amb compàs) OA'=b (amb compàs) A'B'= x AB i A'B' són perpendiculars a la línia OM
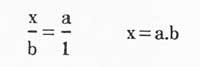
A continuació:
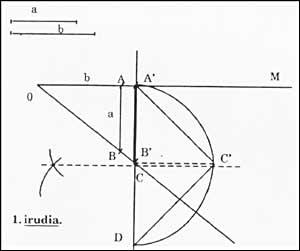
B'D = unitat C, punt mitjà del segment A'D amb centre A'C'D en C B'C', perpendicular a la línia A'D' des de B'C', sent l'altura del triangle recte A'C'D = B'C' A'B'
B'C'= a.b
Aquest era el valor que estàvem buscant.
Prou, per tant, repetir el treball que hem realitzat per a convertir un rectangle en quadrat, substituint als generals a i b pel peu i les altures concretes d'aquest rectangle. A continuació, utilitzant el segment B'C' com a costat, per a completar el quadrat.
Aquesta evolució és interessant en si mateixa, però el més interessant és el fàcil que resulta si pensem a rectificar altres polígons. Així, el rectangle compleix la funció de mediador.
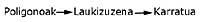
Quadrar un polígon, és a dir, convertir-lo en un quadrat equivalent a la superfície, no és fàcil si volem fer-ho d'una manera correcta, però si utilitzem el rectangle com a element auxiliar intermedi tot és més senzill.
Com el quadrar un polígon i calcular la seva superfície són equivalents, l'interès d'aquesta operació sembla evident.
En aquest número, canviant una mica de tema, volem proposar un nou joc.
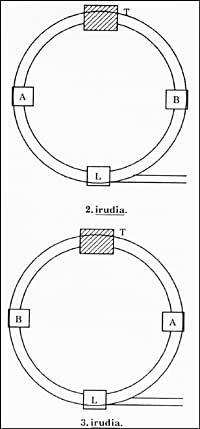
A i B són vagons d'un tren. L, la locomotora. T és un túnel. Al llarg d'aquest túnel es pot arribar a una locomotora però sense cotxes.
La doble línia que apareix en la figura 2 és la via fèrria.
L'essència del joc és com passar de la situació que apareix en la figura 2 a la qual apareix en la figura 3 movent-se el menys possible la locomotora?





