Nikolai I. Lobatxevski (1792-1856): Desde a nada o novo mundo
Poucas veces na historia das matemáticas houbo algo parecido ao agravado polo descubrimento da Xeometría non euclídea. Establecía una crise nas bases, pero, como é costume, saíu reforzado da crise, de tal maneira que partía das novas vías. Como creadores da xeometría non euclídea cítanse principalmente dous nomes: O ruso Nikolai Lobatxevski e o húngaro János Bolyai. O ano 1992 que nos foi entre as celebracións dos famosos séculos deixounos ocultos a outros, e un deles é o segundo do nacemento de Lobatxevski.
Euclides e quinto postulado

No século terceiro a. C. os gregos ofrecéronnos o primeiro libro paira a historia das matemáticas: Elementos de Euclides de Alexandría. Nel analízanse os números e a xeometría. Ademais do tema, o importante é o método, onde se atopa a base do método axiomático deductivo utilizado en Matemáticas. En primeiro lugar, hai afirmacións (postulados ou axiomas) que non deben ser aceptadas e probadas previamente. Posteriormente, aplicando as regras da Lóxica próbanse outras afirmacións (proposicións ou teoremas).
Que condicións hai que esixir aos postulados cando se quere construír una teoría? Por unha banda, é necesario que non sexan contraditorios (é dicir, que non se derive un resultado nin o contrario). Doutra banda, convén non ser demasiado, aínda que isto non arruinaría a teoría. Cando son demasiado? Cando un postulado é consecuencia doutros, pode ser eliminado da lista de postulados e aparecer como teorema, quedando toda a teoría sen modificar.
Euklides utilizou cinco postulados especiais paira a Xeometría. Aínda que a formulación dos elementos é máis xeométrica, en palabras chairas pódense definir como:
- Por calquera dos dous puntos pásase una soa recta.
- Dados dous de forma directa, á beira do primeiro pódese colocar outro congruente co segundo paira darlle una recta máis longa.
- Dados dous puntos diferentes, sempre hai una circunferencia que ten como centro o primeiro e pasa polo segundo.
- Todos os ángulos rectos son congruentes.
- Se una recta corta outras dúas rectas e a suma dos ángulos interiores dun lado é menor que dous rectangulares, únense estendendo as rectas a ese lado.
A pesar de que o catro primeiros postulados parecen aceptarse sen dúbidas, desde hai moito tempo percibiuse que o quinto é especial. No traballo de Euklides tamén se aprecia algo parecido a isto (xa que probou as 28 primeiras proposicións sen utilizar este postulado e só o introduciu cando lle resultou imprescindible).
En séculos posteriores, moitos matemáticos preocupáronse polo quinto postulado e pódense fixar dúas posicións: algunhas, que non gustaron moito a formulación de Euklides e que a substituíron por outra formulación máis “aceptable”. Outros tentaron demostrar que o quinto postulado era consecuencia doutras catro. Moitos deles deron a “demostración”, pero sempre de forma involuntaria, cun postulado alternativo. Nos libros e cursos habituais da xeometría euclídea, uno dos postulados alternativos ocupou o lugar do que Euklides deu: Desde un punto exterior dunha recta pódese realizar una única recta paralela. Por esta razón chámase ao quinto postulado de paralelos.
Un modo de ver que o quinto postulado (en calquera dos seus formulaciones) é consecuencia das anteriores é levalo ao absurdo: considerando que é certo o contrario, chegar a unha contradición. XIX. Antes do século XX, os máis avanzados neste camiño foron a xesuíta italiano Gerolamo Saccheri (1677-1733) e o suízo Johann Heinrich Lambert (1728-1777). Saccherik atopou resultados interesantes pero de aparencia bastante rara (Por suposto, comparando as xeometrías euclídeo coas que estamos afeitos).
Uno deles foi considerado imposible e con iso chegou á conclusión de que o postulado dos paralelos é correcto, tal e como nos ensinou no libro Euklides garbi de todos os erros. Lambert destacou, entre outras cousas, que Saccheri non chegou a contradición e que conseguiu máis resultados pola súa banda. Ademais, percibiu que o quinto postulado non se podía conseguir como consecuencia dos demais e que os resultados do contrario poden ser raros desde a experiencia habitual, pero en ningún caso contraditorios desde o punto de vista da Lóxica. A única razón paira aceptar o postulado dos paralelos sería, por tanto, a conveniencia. Grazas a iso, Lambert foi pioneiro de obras do século seguinte.
XVIII. A finais do século XX, pola súa banda, a opinión do famoso filósofo Kant tamén tivo una gran influencia no debate. Paira Kant non se pode inventar una Xeometría distinta á euclídea, xa que é un coñecemento que temos de antemán (a priori).
Achega de Lobatxevski
Do mesmo xeito que outros moitos, Lobatxevski deu os seus primeiros pasos paira demostrar o postulado dos paralelos e pensou que o conseguiu. Non tardou en tomar outro camiño. O quinto postulado dicía que a experiencia “probaba” e que non se pode dar una demostración fóra dela, ou que non se debe ao catro primeiros postulados. É máis, a substitución doutro catro postulados por outro postulado (non equivalente) e a construción dunha Xeometría distinta á euclídea, tamén sen contradicións. A pesar da liña de Lambert que mencionamos anteriormente, parece que Lobatxevski non coñecía as súas obras.
O postulado alternativo que propuxo era: desde un punto exterior dunha recta pódense facer dúas rectas diferentes que se unen coa anterior. “As superficies e as liñas non están na Natureza, senón na imaxinación”, dirá claramente, deixando a Xeometría á marxe do mundo físico (outra cousa é a que mellor se adapte ás necesidades da Física). Ao principio nomeou verbalmente a Xeometría imaxinaria e, posteriormente, a Pangeometría. Actualmente chámase Xeometría hiperbólica (ás veces tamén Xeometría de Lobatxevski). Os teoremas que se demostran nesta xeometría, como se mencionou anteriormente, non son habituais. Velaquí un par de exemplos:
- A suma dos ángulos dun triángulo é menor que dous rectángulos e a súa superficie é proporcional á que falta para que esa suma sexa dous rectángulos.
- Se os ángulos de dous triángulos son iguais, os triángulos son iguais.

Lobatxevski construíu tamén a Trigonometría correspondente a esta Xeometría, tamén distinta da habitual. Pero hai relacións entre ambas que se apoian entre si, é dicir, se una é posible, a outra tamén.
A pesar de traballar noutros campos, Lobatxevski é coñecido por Xeometría. En febreiro de 1826 falou por primeira vez ao público das súas novas ideas e en 1829 publicou este primeiro tema no Boletín de Kazan. Despois viñeron outros, sempre en ruso, ata que en 1837 sacou una obra en francés no famoso Journal de Crelle (baixo o título de Xeometría Imaxinaria) e tres anos despois una monografía en alemán (Estudos Xeométricos sobre a Teoría dos Paralelos). Un ano antes da súa morte publicou una explicación completa sobre o título Pangeometría, tanto en ruso como en francés.
Bolyai e Gauss
Lobatxevski non foi a única que chegou a estas conclusións. Óbraa “Ciencia do Espazo Absoluto” que o húngaro János Bolyai (1802-1860) dedicou ao seu pai, Wolfgang Bolyaire, á Juventutem Studiosam in Elementa Mathesis (1832-33) similar á de Lobatxevski. Cando o mozo Bolyai en 1823 informou ao seu pai dos seus traballos, díxolle nunha carta: “Fixen descubrimentos tan fascinantes que eu tamén perdín a sorpresa: da nada creei un mundo novo diferente”. Era amigo de Wolfgang Bolyai Gauss e naquela época era o matemático máis famoso. Por iso envioulle o traballo do seu fillo para que lle dese a súa opinión.
A resposta de Gauss é: “Se me poño a dicir que non podo eloxiar este traballo, sorprenderasche, pero non podo facer outra cousa, porque me eloxiaría, porque todo o contido do traballo, o camiño que tomou o teu fillo e os resultados que quere conseguir son case na súa totalidade as reflexións que realicei nos últimos 30-35 anos”. O mozo Bolyai fíxose dano escoitando estas palabras, esperando que Gauss quixéselle roubar os seus resultados. Por outra banda, a pesar da obra de Lobatxevski, nun principio cre que estaba copiada da súa obra. Como consecuencia, abandonou definitivamente as Matemáticas. Pero non é tan raro obter resultados similares de investigadores diferentes sen copiar. Son moi ilustrativas as seguintes palabras de Wolfgang Bolyaire: “Parece que a algunhas consecuencias pódese chegar desde moitos sitios, onde se atopan en diferentes lugares (como ocorreu), tal e como aparecen as violetas na primavera”.
O traballo de Gauss con Xeometrías non euclídicas non se coñece ben, xa que parece que a reacción contra os filósofos kantianos non se atreveu a despedir. Segundo algúns autores, os resultados de Lobatxevski e Bolyaire baséanse en ideas tomadas indirectamente de Gauss e deberiamos considerar a Gauss como o verdadeiro creador da Xeometría non euclídea. Outros, con todo, non o aceptan e afirman que Gauss nunca foi a partir dos primeiros pasos e que hai que confesarlles o que lle corresponde a Lobatxevski e a Bolyai. En calquera caso, parece que Gauss alegrouse ao sacar á rúa a obra dos demais, como logo enxalzou a achega de Riemann en temas similares. Ademais, o nomeamento de Lobatxevski como membro da Sociedade de Ciencias de Göttingen (1842) foi una proposta de Gauss.
Modelos euclídeo
A renovación da xeometría non euclídea na comunidade matemática non se notou rapidamente. Paira iso foron necesarios anos e, sobre todo, a achega do matemático italiano Eugenio Beltrami (1835-1900) deulle o seu lugar en Matemáticas. O feito de non atopar contradicións en lugar do postulado dos paralelos, non aseguraba que non existise, xa que é imposible escribir todos os teoremas que se puidesen deducir. Pero Beltrami descubriu no seo da Xeometría euclídea un modelo que cumpre os requisitos da Xeometría hiperbólica e viceversa. En consecuencia, a Xeometría euclídea e hiperbólica son ambas as posibles ou ambas as imposibles. Deixou totalmente anulada a tendencia a considerar a Xeometría euclídea como una “verdade”.

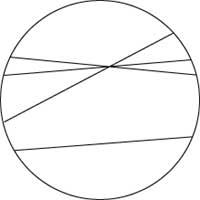
O modelo Beltrami-Klein (sen entrar en detalles) é algo así: dentro dun círculo as rectas son normais (por suposto, as partes que están dentro do círculo), pero a forma de medir as distancias cambia e tamén a de medir ángulos. As “lonxitudes” aumentan a medida que se aproximan ao límite do círculo e, en realidade, a lonxitude dunha corda do círculo é infinita. É fácil observar que neste caso o postulado euclídeo dos paralelos non se cumpre. Neste modelo Poincaré propuxo un cambio. Son rectas, diámetros e anacos de circunferencia (unidos á circunferencia que é o límite do círculo) e os ángulos mídense de forma normal, pero non as distancias.
Digamos, por último, que a diferenza da Física newtoniana, a Física moderna utiliza modelos non euclídeo paira describir o espazo. O lector interesado pola evolución da xeometría non euclídea e os seus modelos euclídeo na revista “Elhuyar” J. Llombart, A. Bernalte e M. Pode ver os seguintes artigos de Ensunza: Borrador histórico de xeometría non euclídea, tomo 11, vol. 2 (1985), pp. 263-271. e modelos euclítricos do plano hiperbólico, tomo 12, vol. 2 (1986), pp. 1-3.
Breve reseña biográfica Nikolai Ivanovitx Lobatxevski naceu o 1 de decembro de 1792 na cidade de Nizhniy-Novgorod (durante varios anos chamada cidade de Gorki). Aínda que tamén se mencionou outra data de nacemento, as investigacións dos historiadores rusos dano como verdadeiro. Con todo, aquel día era o 20 de novembro porque non se aprobou a reforma do calendario gregoriano. Sendo un neno de cinco anos, o seu pai abandonou á súa familia e a súa nai volveu a casa dos seus avós cos seus fillos. Estudou no liceo de Kanzán e en 1807 ingresou na Universidade de Kazan, fundada dous anos antes. En 1811 terminou os seus estudos obtendo o título de Magister e alí propuxéronlle quedar como profesor. En 1816 foi nomeado Catedrático Especial e ese mesmo ano quedou o escribano do curso de Xeometría. Nel non aparecen as ideas que logo desenvolveu. En 1819 recibe a orde de reorganización das bibliotecas e en 1820 é nomeado por primeira vez decano da Facultade de Física e Matemáticas. Foi catedrático en 1822, desde 1825 até 1835. Foi director da biblioteca e reitor da Universidade desde 1827 até 1846. En 1842 foi nomeado membro da Sociedade de Ciencias de Göttingen. En 1846, si por primeira vez fose nomeado catedrático, pasaron 30 anos e debía xubilarse por lei. Como até entón só tiña 53 anos, tentaron obter a exención, pero non foi posible e foi nomeado Representante do Secretario do Distrito Académico de Kazán. En teoría era un posto importante, pero paira el era totalmente burocrático e banal. Abandonou o posto en 1853 e morreu o 23 de febreiro de 1856. |





