Nikolai I. Lobatxevski (1792-1856): Desde la nada el nuevo mundo
Pocas veces en la historia de las matemáticas ha habido algo parecido al agravado por el descubrimiento de la Geometría no euclídea. Establecía una crisis en las bases, pero, como es costumbre, salió reforzado de la crisis, de tal manera que partía de las nuevas vías. Como creadores de la geometría no euclídea se citan principalmente dos nombres: El ruso Nikolai Lobatxevski y el húngaro János Bolyai. El año 1992 que nos ha ido entre las celebraciones de los famosos siglos nos ha dejado ocultos a otros, y uno de ellos es el segundo del nacimiento de Lobatxevski.
Euclides y quinto postulado

En el siglo tercero a. C. los griegos nos ofrecieron el primer libro para la historia de las matemáticas: Elementos de Euclides de Alejandría. En él se analizan los números y la geometría. Además del tema, lo importante es el método, donde se encuentra la base del método axiomático deductivo utilizado en Matemáticas. En primer lugar, hay afirmaciones (postulados o axiomas) que no deben ser aceptadas y probadas previamente. Posteriormente, aplicando las reglas de la Lógica se prueban otras afirmaciones (proposiciones o teoremas).
¿Qué condiciones hay que exigir a los postulados cuando se quiere construir una teoría? Por un lado, es necesario que no sean contradictorios (es decir, que no se derive un resultado ni lo contrario). Por otro lado, conviene no ser demasiado, aunque esto no arruinaría la teoría. ¿Cuándo son demasiado? Cuando un postulado es consecuencia de otros, puede ser eliminado de la lista de postulados y aparecer como teorema, quedando toda la teoría sin modificar.
Euklides utilizó cinco postulados especiales para la Geometría. Aunque la formulación de los elementos es más geométrica, en palabras llanas se pueden definir como:
- Por cualquiera de los dos puntos se pasa una sola recta.
- Dados dos de forma directa, al lado del primero se puede colocar otro congruente con el segundo para darle una recta más larga.
- Dados dos puntos diferentes, siempre hay una circunferencia que tiene como centro el primero y pasa por el segundo.
- Todos los ángulos rectos son congruentes.
- Si una recta corta otras dos rectas y la suma de los ángulos interiores de un lado es menor que dos rectangulares, se unen extendiendo las rectas a ese lado.
A pesar de que los cuatro primeros postulados parecen aceptarse sin dudas, desde hace mucho tiempo se percibió que el quinto es especial. En el trabajo de Euklides también se aprecia algo parecido a esto (ya que probó las 28 primeras proposiciones sin utilizar este postulado y sólo lo introdujo cuando le resultó imprescindible).
En siglos posteriores, muchos matemáticos se han preocupado por el quinto postulado y se pueden fijar dos posiciones: algunas, que no gustaron mucho la formulación de Euklides y que la sustituyeron por otra formulación más “aceptable”. Otros intentaron demostrar que el quinto postulado era consecuencia de otras cuatro. Muchos de ellos dieron la “demostración”, pero siempre de forma involuntaria, con un postulado alternativo. En los libros y cursos habituales de la geometría euclídea, uno de los postulados alternativos ocupó el lugar de lo que Euklides dio: Desde un punto exterior de una recta se puede realizar una única recta paralela. Por esta razón se llama al quinto postulado de paralelos.
Un modo de ver que el quinto postulado (en cualquiera de sus formulaciones) es consecuencia de las anteriores es llevarlo al absurdo: considerando que es cierto lo contrario, llegar a una contradicción. XIX. Antes del siglo XX, los más avanzados en este camino fueron el jesuita italiano Gerolamo Saccheri (1677-1733) y el suizo Johann Heinrich Lambert (1728-1777). Saccherik encontró resultados interesantes pero de apariencia bastante rara (Por supuesto, comparando las geometrías euclídeo con las que estamos acostumbrados).
Uno de ellos fue considerado imposible y con ello llegó a la conclusión de que el postulado de los paralelos es correcto, tal y como nos enseñó en el libro Euklides garbi de todos los errores. Lambert destacó, entre otras cosas, que Saccheri no llegó a contradicción y que consiguió más resultados por su parte. Además, percibió que el quinto postulado no se podía conseguir como consecuencia de los demás y que los resultados del contrario pueden ser raros desde la experiencia habitual, pero en ningún caso contradictorios desde el punto de vista de la Lógica. La única razón para aceptar el postulado de los paralelos sería, por tanto, la conveniencia. Gracias a ello, Lambert fue pionero de obras del siglo siguiente.
XVIII. A finales del siglo XX, por su parte, la opinión del famoso filósofo Kant también tuvo una gran influencia en el debate. Para Kant no se puede inventar una Geometría distinta a la euclídea, ya que es un conocimiento que tenemos de antemano (a priori).
Aportación de Lobatxevski
Al igual que otros muchos, Lobatxevski dio sus primeros pasos para demostrar el postulado de los paralelos y pensó que lo consiguió. No tardó en tomar otro camino. El quinto postulado decía que la experiencia “probaba” y que no se puede dar una demostración fuera de ella, o que no se debe a los cuatro primeros postulados. Es más, la sustitución de otros cuatro postulados por otro postulado (no equivalente) y la construcción de una Geometría distinta a la euclídea, también sin contradicciones. A pesar de la línea de Lambert que hemos mencionado anteriormente, parece que Lobatxevski no conocía sus obras.
El postulado alternativo que propuso era: desde un punto exterior de una recta se pueden hacer dos rectas diferentes que se unen con la anterior. “Las superficies y las líneas no están en la Naturaleza, sino en la imaginación”, dirá claramente, dejando la Geometría al margen del mundo físico (otra cosa es la que mejor se adapte a las necesidades de la Física). Al principio nombró verbalmente la Geometría imaginaria y, posteriormente, la Pangeometría. Actualmente se llama Geometría hiperbólica (a veces también Geometría de Lobatxevski). Los teoremas que se demuestran en esta geometría, como se ha mencionado anteriormente, no son habituales. He aquí un par de ejemplos:
- La suma de los ángulos de un triángulo es menor que dos rectángulos y su superficie es proporcional a la que falta para que esa suma sea dos rectángulos.
- Si los ángulos de dos triángulos son iguales, los triángulos son iguales.

Lobatxevski construyó también la Trigonometría correspondiente a esta Geometría, también distinta de la habitual. Pero hay relaciones entre ambas que se apoyan entre sí, es decir, si una es posible, la otra también.
A pesar de trabajar en otros campos, Lobatxevski es conocido por Geometría. En febrero de 1826 habló por primera vez al público de sus nuevas ideas y en 1829 publicó este primer tema en el Boletín de Kazan. Después vinieron otros, siempre en ruso, hasta que en 1837 sacó una obra en francés en el famoso Journal de Crelle (bajo el título de Geometría Imaginaria) y tres años después una monografía en alemán (Estudios Geométricos sobre la Teoría de los Paralelos). Un año antes de su muerte publicó una explicación completa sobre el título Pangeometría, tanto en ruso como en francés.
Bolyai y Gauss
Lobatxevski no fue la única que llegó a estas conclusiones. La obra “Ciencia del Espacio Absoluto” que el húngaro János Bolyai (1802-1860) dedicó a su padre, Wolfgang Bolyaire, a la Juventutem Studiosam in Elementa Mathesis (1832-33) similar a la de Lobatxevski. Cuando el joven Bolyai en 1823 informó a su padre de sus trabajos, le dijo en una carta: “He hecho descubrimientos tan fascinantes que yo también he perdido la sorpresa: de la nada he creado un mundo nuevo diferente”. Era amigo de Wolfgang Bolyai Gauss y en aquella época era el matemático más famoso. Por eso le envió el trabajo de su hijo para que le diera su opinión.
La respuesta de Gauss es: “Si me pongo a decir que no puedo elogiar este trabajo, te sorprenderás, pero no puedo hacer otra cosa, porque me elogiaría, porque todo el contenido del trabajo, el camino que ha tomado tu hijo y los resultados que quiere conseguir son casi en su totalidad los reflexiones que he realizado en los últimos 30-35 años”. El joven Bolyai se hizo daño escuchando estas palabras, esperando que Gauss le quisiera robar sus resultados. Por otra parte, a pesar de la obra de Lobatxevski, en un principio cree que estaba copiada de su obra. Como consecuencia, abandonó definitivamente las Matemáticas. Pero no es tan raro obtener resultados similares de investigadores diferentes sin copiar. Son muy ilustrativas las siguientes palabras de Wolfgang Bolyaire: “Parece que a algunas consecuencias se puede llegar desde muchos sitios, donde se encuentran en diferentes lugares (como ocurrió), tal y como aparecen las violetas en primavera”.
El trabajo de Gauss con Geometrías no euclídicas no se conoce bien, ya que parece que la reacción contra los filósofos kantianos no se atrevió a despedir. Según algunos autores, los resultados de Lobatxevski y Bolyaire se basan en ideas tomadas indirectamente de Gauss y deberíamos considerar a Gauss como el verdadero creador de la Geometría no euclídea. Otros, sin embargo, no lo aceptan y afirman que Gauss nunca fue a partir de los primeros pasos y que hay que confesarles lo que le corresponde a Lobatxevski y a Bolyai. En cualquier caso, parece que Gauss se alegró al sacar a la calle la obra de los demás, como luego ensalzó la aportación de Riemann en temas similares. Además, el nombramiento de Lobatxevski como miembro de la Sociedad de Ciencias de Göttingen (1842) fue una propuesta de Gauss.
Modelos euclídeo
La renovación de la geometría no euclídea en la comunidad matemática no se notó rápidamente. Para ello fueron necesarios años y, sobre todo, la aportación del matemático italiano Eugenio Beltrami (1835-1900) le dio su lugar en Matemáticas. El hecho de no encontrar contradicciones en lugar del postulado de los paralelos, no aseguraba que no existiera, ya que es imposible escribir todos los teoremas que se pudieran deducir. Pero Beltrami descubrió en el seno de la Geometría euclídea un modelo que cumple los requisitos de la Geometría hiperbólica y viceversa. En consecuencia, la Geometría euclídea e hiperbólica son ambas posibles o ambas imposibles. Dejó totalmente anulada la tendencia a considerar la Geometría euclídea como una “verdad”.

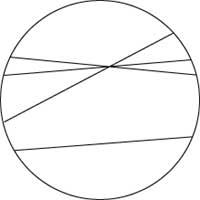
El modelo Beltrami-Klein (sin entrar en detalles) es algo así: dentro de un círculo las rectas son normales (por supuesto, las partes que están dentro del círculo), pero la forma de medir las distancias cambia y también la de medir ángulos. Las “longitudes” aumentan a medida que se aproximan al límite del círculo y, en realidad, la longitud de una cuerda del círculo es infinita. Es fácil observar que en este caso el postulado euclídeo de los paralelos no se cumple. En este modelo Poincaré propuso un cambio. Son rectas, diámetros y trozos de circunferencia (unidos a la circunferencia que es el límite del círculo) y los ángulos se miden de forma normal, pero no las distancias.
Digamos, por último, que a diferencia de la Física newtoniana, la Física moderna utiliza modelos no euclídeo para describir el espacio. El lector interesado por la evolución de la geometría no euclídea y sus modelos euclídeo en la revista “Elhuyar” J. Llombart, A. Bernalte y M. Puede ver los siguientes artículos de Ensunza: Borrador histórico de geometría no euclídea, tomo 11, vol. 2 (1985), pp. 263-271. y modelos euclítricos del plano hiperbólico, tomo 12, vol. 2 (1986), pp. 1-3.
Breve reseña biográfica Nikolai Ivanovitx Lobatxevski nació el 1 de diciembre de 1792 en la ciudad de Nizhniy-Novgorod (durante varios años llamada ciudad de Gorki). Aunque también se ha mencionado otra fecha de nacimiento, las investigaciones de los historiadores rusos lo dan como verdadero. Sin embargo, aquel día era el 20 de noviembre porque no se había aprobado la reforma del calendario gregoriano. Siendo un niño de cinco años, su padre abandonó a su familia y su madre volvió a casa de sus abuelos con sus hijos. Estudió en el liceo de Kanzán y en 1807 ingresó en la Universidad de Kazan, fundada dos años antes. En 1811 terminó sus estudios obteniendo el título de Magister y allí le propusieron quedarse como profesor. En 1816 fue nombrado Catedrático Especial y ese mismo año quedó el escribano del curso de Geometría. En él no aparecen las ideas que luego desarrolló. En 1819 recibe la orden de reorganización de las bibliotecas y en 1820 es nombrado por primera vez decano de la Facultad de Física y Matemáticas. Fue catedrático en 1822, desde 1825 hasta 1835. Fue director de la biblioteca y rector de la Universidad desde 1827 hasta 1846. En 1842 fue nombrado miembro de la Sociedad de Ciencias de Göttingen. En 1846, si por primera vez fuera nombrado catedrático, pasaron 30 años y debía jubilarse por ley. Como hasta entonces sólo tenía 53 años, intentaron obtener la exención, pero no fue posible y fue nombrado Representante del Secretario del Distrito Académico de Kazán. En teoría era un puesto importante, pero para él era totalmente burocrático y banal. Abandonó el puesto en 1853 y murió el 23 de febrero de 1856. |





