A cinta de Möbius
Todos temos en mente a idea de que Matemáticas é una ciencia abstracta. Sempre inmersos en novas teorías, non sabemos até que punto os seus brazos ocultos alárganse. Á parte diso, a maioría dos modelos que se utilizan en Matemáticas non ven, perciben, tocan, ouven e senten na nosa vida como ocorre na física.
A pesar diso, existen contras. Presentámosche una delas, a cinta de Möbius.
Antes de seguir lendo, colle papel e tesoiras.
Paira conseguir a cinta de Möbius colle una longa tira de papel, dá media volta a un extremo (180¼) e logo encola os dous extremos formando o anel. O anel que tes nas túas mans non ten dúas caras ou dous lados, como se podía imaxinar.

Os aneis comúns teñen dúas caras, cada una delas pintada de diferentes cores. O noso anel, a cinta de Möbius, en cambio, non se pode pintar a dúas cores. Si posche a pintar desde un punto, cando acabes descubrirás que pintaches toda a cinta, xa que como dixemos antes a cinta ten una soa cara (só a que pintaches).
O problema non termina aí, senón que pasa o mesmo coa aresta. Desde un punto, toda a aresta corre e volve ao mesmo punto. Así, a cinta de Möbius ten un lado e un bordo.
Esta superficie é especial por outro motivo. Si tense en conta nun punto o vector normal á superficie, tras darlle una volta a través da superficie e paralelo ao bordo, o vector normal quedará en sentido contrario (é dicir, si ao principio estaba a mirar cara á esquerda, despois de darlle a volta estará a mirar cara á dereita). Por tanto, nun mesmo punto terías dous vectores normais. Isto significa que a superficie non é direccional. Por suposto, todo isto debe terse en conta respecto dun sistema de coordenadas tridimensionales.
Esta cinta foi derrubada polo matemático e astrónomo August Ferdinand Möbius en 1858. A partir de entón a cinta de Möbius converteuse nun xoguete de topólogos.
Prepara o papel e as tesoiras porque imos facer traballos manuais.
Si curtas pola metade una cinta normal, obterás dúas cintas iguais. Que pasará si tentas facer o mesmo coa cinta de Möbius? (faino) …Claro! non se conseguen dúas cintas, só una. E a nova cinta resultante é de Möbius ou normal? Ti confirma … aínda que a nova cinta é bifacial, ten dúas espirales, catro xiros de 180º ou dúas xiras completas de 360¼. A nova cinta é máis estreita (a metade do outro) e á vez máis longa (dobre lonxitude). Si córtalo agora de novo pola metade, obterás dúas cintas (máis estreitas pero de igual lonxitude) pero encadeadas (non podes separalas).
Agora imos facer outro traballo.
Colle una tira en papel e divide as dúas caras en tres partes mediante dúas liñas rectas horizontais.
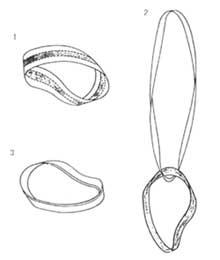
Pinta as partes centrais doutra cor. Agora fórmase a cinta de Möbius. Esta cinta está dividida en tres partes, sendo a central de diferentes cores. Corta a cinta por estas liñas rectas. Una vez terminada, disporás de dúas cintas, una no centro da cinta orixinal e outra nas laterais. A central pintada é a cinta de Möbius. A outra é una cinta con dúas espirales. Ambas teñen a mesma anchura, pero a segunda é máis longa (dobre). Con estas dúas cintas pódese formar una cinta de Möbius de triplo espesor, rodeando a outra (pintada) na maior lonxitude. Como dixemos, esta tripla cinta está formada por outras dúas cintas, a outra (pintada) entre as cintas laterais.
O mesmo efecto pódese conseguir tomando tres tiras de papel e pegando o seis extremos de dous en dous despois de dar a volta a un extremo (180 ¼) como una.
Paira conseguir a cinta de Möbius demos a media (180 ¼) volta a un extremo da tira de papel. Con todo, non é esta a única posibilidade de conseguir una cinta dun só rostro. E é que si damos a volta ao extremo cunha t’erdi (540¼) ou dúas voltas cunha t’erdi (900¼), ou…, podemos conseguir una cinta deste tipo.
Por iso, podemos dividir as cintas en dúas clases: una cara e dúas caras. O primeiro conseguirase dando a un extremo un número impar de medias; o segundo, cando o número de medias sexa par.
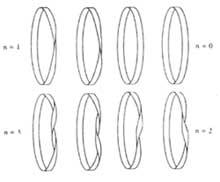
As voltas pódense dar cara á esquerda ou cara á dereita. As cintas así obtidas son homeomorfos na topología, equivalentes na nosa lingua. Con todo, non se pode converter una noutra.
Así as cintas dunha cara cortadas polo centro darannos una cinta. As características da nova xingola son as seguintes: ten a metade da anchura da orixinal e o dobre da lonxitude; é una cinta de dúas caras; se a cinta orixinal ten media volta n, a nova cinta terá 2n+2 voltas ou n+1 espirales (volta completa 360¼). Por tanto, a cinta de Möbius (n=1) daranos una cinta de catro voltas ou dúas espirales.
Pola contra, as cintas de dúas caras dannos dúas cintas iguais despois da metade (antes non quixemos utilizar este verbo). Características das novas cintas: teñen a mesma lonxitude que o orixinal e a metade da súa anchura; son cintas de dúas caras; teñen tantas voltas como as orixinais; no caso de n=0 as cintas aparecen soltas, nos demais casos conséguense dúas cintas encadeadas.
Realizáronse numerosos intentos paira utilizar industrialmente a cinta de Möbius, como a cinta transportadora que Le de Forest inventou en 1923 una película con esta forma, filtros autolimpiantes, cintas calcinantes, cintas transportadoras paira a máquina de escribir, etc.
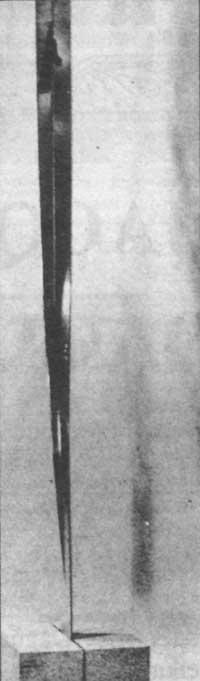
En artes tamén podemos ver algúns exemplos: o M.C que coñeces neste apartado. Realizadas polo artista Escher; o escultor suízo Max Bill; a cinta de dous metros de altura situada fronte ao Museo de Historia e Tecnoloxía de Washington D.C. xira sobre si mesmo.
Nunha cinta de Möbius poderíase escribir a seguinte frase incompleta: “Nunha ocasión había un conto que comezaba así…”
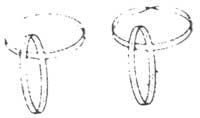
As estruturas de papel representadas na figura 5 son similares, a da esquerda está formada por dous aneis normais. O da dereita é un anel normal e una cinta de Möbius. Recorta ambas as liñas de puntos e compara os resultados obtidos.
Até aquí falamos da cinta de Möbius. Con todo, non podemos deixar de mencionar outro modelo matemático relacionado coa cinta de Möbius. A cinta de Möbius obtíñase utilizando una tira de papel. Con todo, este novo modelo podería conseguirse pegando dúas cintas de Möbius con cola. O novo modelo, denominado botella de Klein, foi ideado polo matemático Felix Klein.

A botella de Klein non se pode construír tan facilmente como a cinta de Möbius. Con todo, supondo que o cristal se pode reducir e tirar como queremos, pódese obter a botella tal e como se ve na imaxe final. A botella resultante ten un buraco e una aresta. Teoricamente pódese conseguir sen buracos nin arestas, aínda que na realidade (fisicamente) non é posible. Trátase dunha botella que se caracteriza por ter una soa cara, a mesma característica que a cinta de Möbius.
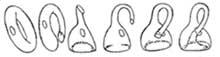
Supuxemos que o material paira construír a botella de Klein, o cristal, é moi flexible. Na Topología, rama das matemáticas, este tipo de supostos son lexítimos. De feito, a Topología estuda as propiedades posicionales invariantes aos cambios de tamaño e formas. Quizá a forma máis sinxela de definir as propiedades topológicas é dicir que son propiedades xeométricas que permanecen invariables ás extensións e resumos.





