Le ruban de Möbius
Nous avons tous à l'esprit l'idée que les mathématiques est une science abstraite. Toujours immergés dans de nouvelles théories, nous ne savons pas à quel point leurs bras cachés s'allongent. En dehors de cela, la plupart des modèles qui sont utilisés en mathématiques ne sont pas vus, perçoivent, touchent, entendent et se sentent dans notre vie comme il arrive en physique.
Malgré cela, il y a des inconvénients. Voici l'une d'entre elles, la bande de Möbius.
Avant de continuer à lire, prenez du papier et des ciseaux.
Pour obtenir le ruban de Möbius, prenez une longue bande de papier, faites demi-tour à une extrémité (180¼), puis collez les deux extrémités formant l'anneau. L'anneau que vous avez dans vos mains n'a pas deux faces ou deux côtés, comme vous pouvez l'imaginer.

Les anneaux communs ont deux faces, chacune peinte de différentes couleurs. Notre bague, la bande de Möbius, en revanche, ne peut pas être peinte à deux couleurs. Si vous vous mettez à peindre à partir d'un point, quand vous avez fini, vous découvrirez que vous avez peint tout le ruban, car comme nous l'avons déjà dit, le ruban a un seul visage (seulement celui que vous avez peint).
Le problème ne s'arrête pas là, mais passe la même chose avec l'arête. D'un point, toute l'arête court et revient au même point. Ainsi, la bande de Möbius a un côté et un bord.
Cette surface est spéciale pour une autre raison. Si l'on tient compte à un point du vecteur normal à la surface, après avoir fait un tour à travers la surface et parallèle au bord, le vecteur normal restera dans le sens inverse (c'est-à-dire si au début il regardait vers la gauche, après le tour il regardera vers la droite). Par conséquent, à un même point, vous auriez deux vecteurs normaux. Cela signifie que la surface n'est pas directionnelle. Bien sûr, tout cela doit être pris en compte par rapport à un système de coordonnées tridimensionnelles.
Ce ruban a été abattu par le mathématicien et astronome August Ferdinand Möbius en 1858. Depuis lors, le ruban de Möbius est devenu un jouet de topologos.
Préparez le papier et les ciseaux parce que nous allons faire des travaux manuels.
Si vous coupez en deux une bande normale, vous obtiendrez deux bandes identiques. Que se passera-t-il si vous essayez de faire de même avec le ruban Möbius ? (faites-le) … Bien sûr! ne pas obtenir deux bandes, juste un. Et le nouveau ruban obtenu est de Möbius ou normal ? Vous confirmez … même si le nouveau ruban est bifacial, il a deux spirales, quatre tours de 180° ou deux tournées complètes de 360¼. La nouvelle bande est plus étroite (la moitié de l'autre) et plus longue (double longueur). Si vous le coupez à nouveau en deux, vous obtiendrez deux bandes (plus étroites mais de même longueur) mais enchaînées (vous ne pouvez pas les séparer).
Maintenant, nous allons faire un autre travail.
Prenez une bande sur papier et divisez les deux faces en trois parties par deux lignes droites horizontales.
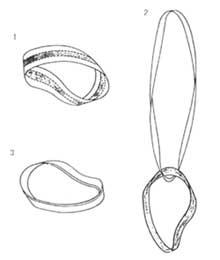
Peignez les parties centrales d'une autre couleur. Maintenant, la bande de Möbius est formée. Ce ruban est divisé en trois parties, étant la centrale de différentes couleurs. Coupez la bande par ces lignes droites. Une fois terminé, vous disposerez de deux bandes, l'une au centre du ruban original et l'autre sur les côtés. La centrale peinte est le ruban de Möbius. L'autre est une bande avec deux spirales. Les deux ont la même largeur, mais la seconde est plus longue (double). Avec ces deux bandes, vous pouvez former un ruban Möbius triple épaisseur, entourant l'autre (peint) sur la plus grande longueur. Comme nous l'avons dit, cette triple bande est formée de deux autres bandes, l'autre (peinte) entre les bandes latérales.
Le même effet peut être obtenu en prenant trois bandes de papier et en collant les six extrémités de deux sur deux après avoir tourné à une extrémité (180 ¼) comme une.
Pour obtenir la bande de Möbius nous avons donné la moyenne (180 ¼) retour à une extrémité de la bande de papier. Cependant, ce n'est pas la seule possibilité d'obtenir un ruban d'un seul visage. Et c’est que si on tourne à l’extrême avec un t’erdi (540¼) ou deux tours avec un t’erdi (900¼), ou…, on peut obtenir un tel ruban.
C'est pourquoi nous pouvons diviser les bandes en deux classes : une face et deux faces. Le premier sera obtenu en donnant à une extrémité un nombre impair de moyennes ; le deuxième, quand le nombre de moyennes est pair.
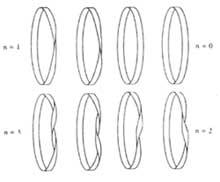
Les tours peuvent être donnés vers la gauche ou vers la droite. Les bandes ainsi obtenues sont des homéomorphes dans la topologie, équivalents dans notre langue. Cependant, vous ne pouvez pas convertir l'un en l'autre.
Ainsi les bandes d'une face coupées par le centre nous donneront une bande. Les caractéristiques de la nouvelle xingole sont les suivantes: il a la moitié de la largeur de l'original et le double de la longueur; c'est une bande à deux faces; si la bande originale a demi-tour n, la nouvelle bande aura 2n+2 tours ou n+1 spirales (tour complet 360¼). Par conséquent, la bande de Möbius (n=1) nous donnera une bande de quatre tours ou deux spirales.
Au contraire, les bandes à deux faces nous donnent deux bandes égales après la moitié (avant nous n'avons pas voulu utiliser ce verbe). Caractéristiques des nouveaux rubans: ils ont la même longueur que l'original et la moitié de leur largeur; ils sont des rubans à deux faces; ils ont autant de tours que les originaux; dans le cas de n=0 les rubans apparaissent lâches, dans les autres cas on obtient deux rubans enchaînés.
De nombreuses tentatives ont été faites pour utiliser industriellement le ruban Möbius, comme le convoyeur que Lee de Forest a inventé en 1923 un film sous cette forme, des filtres autonettoyants, des rubans calcinants, des convoyeurs pour la machine à écrire, etc.
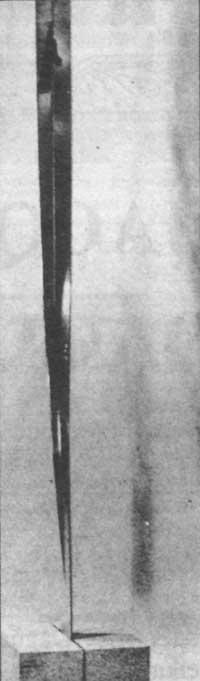
Dans les arts nous pouvons également voir quelques exemples : le M.C que vous connaissez dans cette section. Réalisé par l'artiste Escher; le sculpteur suisse Max Bill; le ruban de deux mètres de haut situé en face du Musée d'histoire et de technologie de Washington D.C. tourne sur lui-même.
Sur une bande de Möbius on pourrait écrire la phrase suivante incomplète: “Une fois, il y avait un conte qui commençait ainsi…”
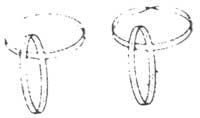
Les structures de papier représentées dans la figure 5 sont similaires, celle de gauche est formée de deux anneaux normaux. Celui sur la droite est un anneau normal et un ruban de Möbius. Coupez les deux lignes de points et comparez les résultats obtenus.
Jusqu'ici, nous avons parlé de la bande de Möbius. Cependant, nous ne pouvons manquer de mentionner un autre modèle mathématique lié à la bande de Möbius. La bande de Möbius était obtenue en utilisant une bande de papier. Cependant, ce nouveau modèle pourrait être obtenu en collant deux bandes de Möbius avec colle. Le nouveau modèle, appelé bouteille de Klein, a été conçu par le mathématicien Felix Klein.

La bouteille de Klein ne peut pas être construite aussi facilement que la bande de Möbius. Cependant, en supposant que le verre peut être réduit et jeté comme nous le voulons, vous pouvez obtenir la bouteille comme on le voit dans l'image finale. La bouteille qui en résulte a un trou et une arête. Théoriquement, il peut être obtenu sans trous ni arêtes, mais en réalité (physiquement) il n'est pas possible. Il s'agit d'une bouteille qui se caractérise par une seule face, la même caractéristique que la bande de Möbius.
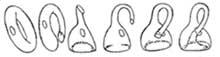
Nous avons supposé que le matériau pour construire la bouteille de Klein, le verre, est très flexible. En topologie, branche des mathématiques, ce genre de cas sont légitimes. En fait, la topologie étudie les propriétés positionnelles invariantes aux changements de taille et de formes. Peut-être la façon la plus simple de définir les propriétés topologiques est que ce sont des propriétés géométriques qui restent invariables à des extensions et des résumés.





