La cinta de Möbius
Todos tenemos en mente la idea de que Matemáticas es una ciencia abstracta. Siempre inmersos en nuevas teorías, no sabemos hasta qué punto sus brazos ocultos se alargan. Aparte de eso, la mayoría de los modelos que se utilizan en Matemáticas no se ven, perciben, tocan, oyen y se sienten en nuestra vida como ocurre en la física.
A pesar de ello, existen contras. Te presentamos una de ellas, la cinta de Möbius.
Antes de seguir leyendo, coge papel y tijeras.
Para conseguir la cinta de Möbius coge una larga tira de papel, da media vuelta a un extremo (180¼) y luego encola los dos extremos formando el anillo. El anillo que tienes en tus manos no tiene dos caras o dos lados, como se podía imaginar.

Los anillos comunes tienen dos caras, cada una de ellas pintada de diferentes colores. Nuestro anillo, la cinta de Möbius, en cambio, no se puede pintar a dos colores. Si te pones a pintar desde un punto, cuando acabes descubrirás que has pintado toda la cinta, ya que como hemos dicho antes la cinta tiene una sola cara (sólo la que has pintado).
El problema no termina ahí, sino que pasa lo mismo con la arista. Desde un punto, toda la arista corre y vuelve al mismo punto. Así, la cinta de Möbius tiene un lado y un borde.
Esta superficie es especial por otro motivo. Si se tiene en cuenta en un punto el vector normal a la superficie, tras darle una vuelta a través de la superficie y paralelo al borde, el vector normal quedará en sentido contrario (es decir, si al principio estaba mirando hacia la izquierda, después de darle la vuelta estará mirando hacia la derecha). Por lo tanto, en un mismo punto tendrías dos vectores normales. Esto significa que la superficie no es direccional. Por supuesto, todo esto debe tenerse en cuenta respecto a un sistema de coordenadas tridimensionales.
Esta cinta fue derribada por el matemático y astrónomo August Ferdinand Möbius en 1858. A partir de entonces la cinta de Möbius se ha convertido en un juguete de topólogos.
Prepara el papel y las tijeras porque vamos a hacer trabajos manuales.
Si cortas por la mitad una cinta normal, obtendrás dos cintas iguales. ¿Qué pasará si intentas hacer lo mismo con la cinta de Möbius? (hazlo) …¡Claro! no se consiguen dos cintas, sólo una. ¿Y la nueva cinta resultante es de Möbius o normal? Tú confirma … aunque la nueva cinta es bifacial, tiene dos espirales, cuatro giros de 180º o dos giras completas de 360¼. La nueva cinta es más estrecha (la mitad del otro) y a la vez más larga (doble longitud). Si lo cortas ahora de nuevo por la mitad, obtendrás dos cintas (más estrechas pero de igual longitud) pero encadenadas (no puedes separarlas).
Ahora vamos a hacer otro trabajo.
Coge una tira en papel y divide las dos caras en tres partes mediante dos líneas rectas horizontales.
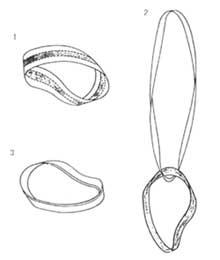
Pinta las partes centrales de otro color. Ahora se forma la cinta de Möbius. Esta cinta está dividida en tres partes, siendo la central de diferentes colores. Corta la cinta por estas líneas rectas. Una vez terminada, dispondrás de dos cintas, una en el centro de la cinta original y otra en las laterales. La central pintada es la cinta de Möbius. La otra es una cinta con dos espirales. Ambas tienen la misma anchura, pero la segunda es más larga (doble). Con estas dos cintas se puede formar una cinta de Möbius de triple espesor, rodeando la otra (pintada) en la mayor longitud. Como hemos dicho, esta triple cinta está formada por otras dos cintas, la otra (pintada) entre las cintas laterales.
El mismo efecto se puede conseguir tomando tres tiras de papel y pegando los seis extremos de dos en dos después de dar la vuelta a un extremo (180 ¼) como una.
Para conseguir la cinta de Möbius hemos dado la media (180 ¼) vuelta a un extremo de la tira de papel. Sin embargo, no es ésta la única posibilidad de conseguir una cinta de un solo rostro. Y es que si damos la vuelta al extremo con una t’erdi (540¼) o dos vueltas con una t’erdi (900¼), o…, podemos conseguir una cinta de este tipo.
Por ello, podemos dividir las cintas en dos clases: una cara y dos caras. El primero se conseguirá dando a un extremo un número impar de medias; el segundo, cuando el número de medias sea par.
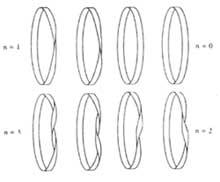
Las vueltas se pueden dar hacia la izquierda o hacia la derecha. Las cintas así obtenidas son homeomorfos en la topología, equivalentes en nuestra lengua. Sin embargo, no se puede convertir una en otra.
Así las cintas de una cara cortadas por el centro nos darán una cinta. Las características de la nueva xingola son las siguientes: tiene la mitad de la anchura de la original y el doble de la longitud; es una cinta de dos caras; si la cinta original tiene media vuelta n, la nueva cinta tendrá 2n+2 vueltas o n+1 espirales (vuelta completa 360¼). Por tanto, la cinta de Möbius (n=1) nos dará una cinta de cuatro vueltas o dos espirales.
Por el contrario, las cintas de dos caras nos dan dos cintas iguales después de la mitad (antes no hemos querido utilizar este verbo). Características de las nuevas cintas: tienen la misma longitud que el original y la mitad de su anchura; son cintas de dos caras; tienen tantas vueltas como las originales; en el caso de n=0 las cintas aparecen sueltas, en los demás casos se consiguen dos cintas encadenadas.
Se han realizado numerosos intentos para utilizar industrialmente la cinta de Möbius, como la cinta transportadora que Lee de Forest inventó en 1923 una película con esta forma, filtros autolimpiantes, cintas calcinantes, cintas transportadoras para la máquina de escribir, etc.
En artes también podemos ver algunos ejemplos: el M.C que conoces en este apartado. Realizadas por el artista Escher; el escultor suizo Max Bill; la cinta de dos metros de altura situada frente al Museo de Historia y Tecnología de Washington D.C. gira sobre sí mismo.
En una cinta de Möbius se podría escribir la siguiente frase incompleta: “En una ocasión había un cuento que comenzaba así…”
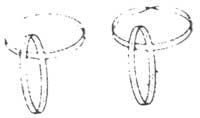
Las estructuras de papel representadas en la figura 5 son similares, la de la izquierda está formada por dos anillos normales. El de la derecha es un anillo normal y una cinta de Möbius. Recorta ambas líneas de puntos y compara los resultados obtenidos.
Hasta aquí hemos hablado de la cinta de Möbius. Sin embargo, no podemos dejar de mencionar otro modelo matemático relacionado con la cinta de Möbius. La cinta de Möbius se obtenía utilizando una tira de papel. Sin embargo, este nuevo modelo podría conseguirse pegando dos cintas de Möbius con cola. El nuevo modelo, denominado botella de Klein, ha sido ideado por el matemático Felix Klein.

La botella de Klein no se puede construir tan fácilmente como la cinta de Möbius. Sin embargo, suponiendo que el cristal se puede reducir y tirar como queremos, se puede obtener la botella tal y como se ve en la imagen final. La botella resultante tiene un agujero y una arista. Teóricamente se puede conseguir sin agujeros ni aristas, aunque en la realidad (físicamente) no es posible. Se trata de una botella que se caracteriza por tener una sola cara, la misma característica que la cinta de Möbius.
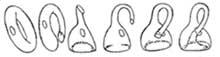
Hemos supuesto que el material para construir la botella de Klein, el cristal, es muy flexible. En la Topología, rama de las matemáticas, este tipo de supuestos son legítimos. De hecho, la Topología estudia las propiedades posicionales invariantes a los cambios de tamaño y formas. Quizá la forma más sencilla de definir las propiedades topológicas es decir que son propiedades geométricas que permanecen invariables a las extensiones y resúmenes.





