Mathematica Mathematica
Pour connaître quelque chose de l'histoire, disons que la première version de Mathematica est sortie en 1988 pour les ordinateurs Apple Macintosh, mais a été rapidement développé pour une utilisation sur d'autres plates-formes: IBM PC, Silicon Graphics, Hewlett Paccard, Sun, etc… La deuxième version a été lancée en 1991 et a été celle qui a été utilisée sur les ordinateurs jusqu'en septembre de l'année dernière, à la fin de la troisième version: Mathematica 3.0. Ils sont fondamentalement similaires. La modification la plus significative est l'ensemble des caractères utilisés pour exprimer des expressions mathématiques ( mathematical typesetting ). Les nouveaux symboles mathématiques ont une signification typographique et fonctionnelle. Par exemple, chaque opération avait son code ou sa clé de mot dans les versions précédentes. Dans cette dernière version, la plupart des opérations peuvent être exprimées par mot clé et par écrit mathématique. Par exemple :
Power[2,10] ou 210 Sqrt[28] ou « w28
En même temps, les fichiers créés par Mathematica version 3.0 sont des expressions propres à Mathematica, ce qui permet de les manipuler dans des programmes comme n'importe quelle autre expression symbolique. La capacité de calcul est également plus élevée dans cette version, avec une vitesse d'exécution plus élevée et moins de mémoire dans certaines opérations. De nouvelles fonctions et outils ont également été intégrés et d'autres ont été améliorés. Notez également qu'il est nécessaire d'avoir un ordinateur suffisant pour utiliser cette dernière version confortablement, car ils recommandent 16 Mo de Ram et 75 Mo de disque dur. Pour terminer, indiquer que tous les exemples à exposer seront réalisés avec Mathematica version 3.0.
Son principal avantage est sa capacité à travailler avec des expressions symboliques. “Tout peut être exprimé comme symbolique expressive”. C'était l'idée de base de ceux qui ont construit Mathematica. Par conséquent, il peut être utilisé comme calculatrice numérique ou symbolique, sert à afficher les données et les fonctions, offre un langage de haut niveau pour écrire des programmes, est un environnement idéal pour l'analyse des données et, surtout, est un outil capable de combiner du texte, des graphiques (si vous voulez animés) et des formules actives dans des documents interactifs. Vous pouvez également gérer le son, car il permet de définir des objets sonores.
Mathematica peut effectuer trois types d'opérations : numériques, symboliques et graphiques. En ce qui concerne le calcul numérique, le moyen le plus simple d'utiliser Mathematica est de l'utiliser comme calculatrice. Cependant, les calculatrices ont une précision fixe, c'est-à-dire que le nombre de chiffres décimaux est fixé à l'avance, tandis que dans Mathematica on peut indiquer dans l'ordre même la précision requise au calcul. Dans l'exemple suivant, ceux qui sont en gras sont les commandes passées à Mathematica et en lettre simple les réponses données par Mathematica (les mots-clés In:=[nombre] et Out=[nombre] qui apparaissent précédemment sont ajoutés par le programme lui-même pour différencier les entrées et sorties, relier chaque sortie à l'entrée correspondante et ensuite faire des références à ces entrées/sorties par un nombre simple).
l n[1]:=log[4Pi] Out[1]=log(4cer) l[2]:=n[Log[4ler]]] Out[2]=2.53102 ln[3]:=n[Log 4cer],10]
En outre, l'ensemble des opérations est plus grand, environ 750 fonctions de intégrante elliptique et Bessel, y compris la factorisation des fonctions hypergéométriques et des nombres entiers.
Vous pouvez également appliquer des opérations numériques comme l'intégration numérique, la programmation linéaire, etc. En outre, il fournit des solutions aux équations algébriques et aux équations différentielles conventionnelles.
Parmi les calculs symboliques qu'il réalise se distingue la manipulation de formules algébriques. Le polynôme et l'expression rationnelle peuvent être simplifiés, élargis ou factorisés. Vous pouvez également trouver des solutions algébriques des équations polynomiales et des systèmes d'équations. Contrairement à la deuxième version, dans la dernière version il incorpore des facilités pour travailler avec des matrices et il n'est pas obligatoire d'utiliser des tables pour la définition des matrices.
Il évalue symboliquement les intégrales et leurs dérivés, maniant des approximations par séries et calculant des limites.
Dans le domaine des graphiques, il réalise des graphiques bidimensionnels et tridimensionnels, des plots densité et contour (visions supérieures), tant des fonctions que des listes de données. De plus, il existe de nombreuses possibilités de contrôler les détails du graphique, par exemple. : mise au point, couleur, luminosité…
Il dispose d'une bibliothèque pour graphiques prédéfinis, qui à travers une série d'ordres primitifs d'objets géométriques (par exemple, polygones) montre les objets graphiquement par une représentation symbolique.
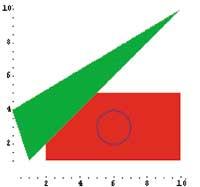
} rectangle = Graphics[{RGolor[1,0,0], Rectangle[{2,1}, 10, 5}] rectangle = Graphics[{RGBCcolor[1,0,0], Angle[{2,1}, 5}] bcGraphics
• Graphics•
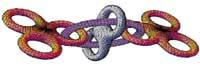
Tous les graphiques formés par Mathematica ont le format PostScript (PS) de sorte qu'ils peuvent être transportés vers d'autres applications.
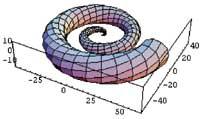
ParametricPlot3D[{uCos[u] (4+Cos[v+u]), uSin[u] (4+Cos[v+u]), uSin[v+u]}, {u,0,4}, {v,0,2}, PlotPoints {60,12}]
En outre, il a son propre langage, de sorte que vous pouvez écrire des programmes dans le langage Mathematica.
D'autre part, le langage de programmation Mathematica admet différents styles de programmation : procédural, avec structure de blocs, commandes conditionnelles et bandes répétitives ; fonctionnel, avec agents fonctionnels ; programmation basée sur des règles, assimilation modale ( pattern matching ) et programmation orientée objet.
Le programme Mathematica est structuré en deux grandes parties: le noyau et le front-end. Kernel est le noyau, la partie chargée de réaliser les calculs, et le front-end n'est que la partie qui interagit avec l'utilisateur, une interface confortable pour l'utilisateur et dont les commandes sont envoyées au noyau. Si le noyau est le même sur toutes les plates-formes informatiques, nous pourrions le trouver avec différents front-end, qui a été optimisé pour certaines architectures. Ce front-end offre à l’utilisateur des documents appelés “notebook”, c’est-à-dire du texte échelonné par priorité, des graphiques animés et des expressions mathématiques (formules, etc.) Cahiers qu'il admet. Dans ces cahiers on peut élaborer du matériel pédagogique ou d'un autre type, et la caractéristique la plus singulière est que, en plus des explications écrites, on peut réaliser des opérations dans ces cahiers.
En général, Mathematica se caractérise par sa compatibilité communicative avec de nombreux autres programmes. Cela vous permet de lire des données dans différents formats (C, Fortran, TEX). En utilisant la norme MathLink, vous pouvez échanger des données et des commandes avec d'autres applications.
Pendant l'exécution du mathematica, certaines bibliothèques stardi sont chargées. Elles comprennent des fonctions de calcul mathématique de base, des graphiques et d'autres domaines mathématiques communs. Cependant, Mathematica dispose également d'autres bibliothèques plus spécifiques qui ne sont pas chargées au démarrage du programme. La charge des packages définis pour leurs besoins spécifiques est à la disposition de l'utilisateur. Par exemple, supposons que nous ayons défini les fonctions « factorielle » et « exponentielle » dans la bibliothèque « gurelib ».
DeclarePackage[“Calculus`gurelib`”,{”factorial”,”exponentiel”}]
Une fois la commande exécutée, nous pourrons utiliser les opérations factorielle et exponentielle selon la norme d'ordre donnée dans la définition. La bibliothèque que Mathematica a chargée à tout moment est stockée dans la variable globale $Packages.
Comme il ne pouvait pas être autrement, Mathematica a également sa propre adresse Web, où vous pouvez trouver des informations, des graphiques et des dernières nouvelles: http://www.wolfram.com





