Mathematica
Per a conèixer una mica de la història, diguem que la primera versió de Mathematica va sortir en 1988 per als ordinadors Apple Macintosh, però va anar ràpidament desenvolupada per al seu ús en altres plataformes: IBM PC, Silicon Graphics, Hewlett Paccard, Sun, etc… La segona versió es va llançar en 1991 i ha estat la que s'ha utilitzat en els ordinadors fins a setembre de l'any passat, quan va finalitzar la tercera versió: Mathematica 3.0. Són bàsicament similars. La modificació més significativa és el conjunt de caràcters utilitzats per a expressar expressions matemàtiques ( mathematical typesetting ). Els nous símbols matemàtics tenen un significat tipogràfic i funcional. Per exemple, cada operació tenia el seu codi o clau de paraula en versions anteriors. En aquesta última versió, la majoria de les operacions es poden expressar tant per clau de paraula com per escriptura matemàtica. Per exemple:
Power[2,10] o 210 Sqrt[28 ] o “w28
Al mateix temps, els fitxers creats per Mathematica versió 3.0 són expressions pròpies de Mathematica, la qual cosa permet manipular-los en programes com qualsevol altra expressió simbòlica. La capacitat de computació també és major en aquesta versió, amb major velocitat d'execució i menor memòria en algunes operacions. També s'han incorporat noves funcions i eines, i s'han millorat unes altres ja conegudes. Esmentar també que és necessari disposar d'un ordinador maco suficient per a utilitzar aquesta última versió de manera còmoda, ja que recomanen 16 MB de Ram i 75 MB de disc dur. Per a finalitzar, indicar que tots els exemples que s'exposaran seran realitzats amb Mathematica versió 3.0.
El seu principal avantatge és la seva capacitat per a treballar amb expressions simbòliques. “Qualsevol cosa pot expressar-se com a simbòlica expressiva”. Aquesta va ser la idea bàsica dels quals van construir Mathematica. Per tant, pot utilitzar-se com a calculadora numèrica o simbòlica, serveix per a visualitzar dades i funcions, ofereix un llenguatge d'alt nivell per a escriure programes, és un entorn idoni per a l'anàlisi de dades i, sobretot, és una eina capaç de combinar text, gràfics (si es desitja animats) i fórmules actives en documents interactius. També pot manejar el so, ja que permet definir objectes de so.
Mathematica pot realitzar tres tipus d'operacions: numèriques, simbòliques i gràfiques. Quant a la computació numèrica, la forma més senzilla d'utilitzar Mathematica és utilitzar-la com a calculadora. No obstant això, les calculadores tenen una precisió fixa, és a dir, el nombre de xifres decimals està fixat per endavant, mentre que en Mathematica es pot indicar en la pròpia ordre la precisió requerida al càlcul. En el següent exemple els que estan en negreta són les comandes realitzades a Mathematica i en lletra simple les respostes donades per Mathematica (les paraules clau In:=[número] i Out=[número] que apareixen anteriorment són afegides pel propi programa per a diferenciar les entrades i sortides, relacionar cada sortida amb l'entrada corresponent i després fer referències a aquestes entrades/sortides mitjançant un número senzill).
l n[1]:=log[4Pi] Out[1]=log(4cer) l[2]:=n[Log[4ler]] Out[2]=2.53102 ln[3]:=n[Log 4cer],10] Out[3]=2.531024247
D'altra banda, el conjunt d'operacions és major, unes 750 funcions d'integral el·líptica i Bessel, incloent la factorització de funcions hipergeomètriques i nombres enters.
També pot aplicar operacions numèriques com a integració numèrica, programació lineal, etc. A més, proporciona solucions a equacions algebraiques i a equacions diferencials convencionals.
Entre les computacions simbòliques que realitza destaca la manipulació de fórmules algebraiques. El polinomi i l'expressió racional poden simplificar-se, estendre's o factorizarse. També pot trobar solucions algebraiques d'equacions polinomiales i sistemes d'equacions. A diferència de la segona versió, en l'última versió incorpora facilitats per a treballar amb matrius i no és obligatori l'ús de taules per a la definició de matrius.
Així mateix, avalua simbòlicament les integrals i els seus derivats, manejant aproximacions per sèries i calculant límits.
En el camp dels gràfics, realitza gràfics bidimensionals i tridimensionals, plots densitat i contour (visions superiors), tant des de funcions com des de llistes de dades. A més, existeixen nombroses possibilitats de controlar els detalls del gràfic, p. ex. : enfocament, color, lluminositat…
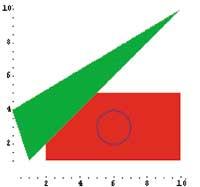
Disposa d'una biblioteca per a gràfics predefinits, que mitjançant una sèrie d'ordres primitives d'objectes geomètrics (per exemple, polígons) mostra els objectes gràficament mitjançant una representació simbòlica.
} rectangle = Graphics[{RGBColor[1,0,0], Rectangle[{2,1}, 10, 5}] rectangle = Graphics[{RGBCcolor[1,0,0], Angle[{2,1}, {10, 5}]> Graphics
•Graphics•
Tots els gràfics formats per Mathematica tenen format PostScript (PS) pel que poden ser transportats a altres aplicacions.
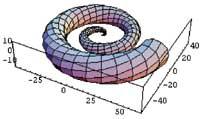
ParametricPlot3D[{uCos[o] (4+Cos[v+o]), uSin[o] (4+Cos[v+o]), uSin[v+o]}, {o,0,4>}, {v,0,2>}, PlotPoints > {60,12}]
A més, té un llenguatge propi, per la qual cosa es poden escriure programes en el llenguatge Mathematica.
D'altra banda, el llenguatge de programació Mathematica admet diferents estils de programació: procedimental, amb estructura de blocs, ordres condicionals i fleixos repetitius; funcional, amb agents funcionals; programació basada en regles, equiparació modal ( pattern matching ) i programació orientada a objectes.
El programa Mathematica s'estructura en dues grans parts: el kernel i el front-end. Kernel és el nucli, la part encarregada de realitzar els càlculs, i el front-end és només la part que interacciona amb l'usuari, una interfície còmoda per a l'usuari i les ordres del qual són enviades al kernel. Si el kernel és el mateix en totes les plataformes d'ordinador, podríem trobar-ho amb diferents front-end, que s'ha optimitzat per a certes arquitectures. Aquest front-end ofereix a l'usuari documents denominats “notebook”, és a dir, text escalonat per prioritat, gràfics animats i expressions matemàtiques (fórmules, etc.) Quaderns que admet. En aquests quaderns es pot elaborar material pedagògic o d'un altre tipus, i la característica més singular és que, a més de les explicacions escrites, es poden realitzar operacions en aquests.
En general, Mathematica es caracteritza per la seva compatibilitat comunicativa amb molts altres programes. Això li permet llegir dades en diferents formats (C, Fortran, TEX). En utilitzar l'estàndard MathLink, pot intercanviar dades i comandos amb altres aplicacions.
Durant l'execució del mathematica es carreguen algunes biblioteques estardíes. En elles s'inclouen funcions bàsiques de càlcul matemàtic, gràfics i altres àrees matemàtiques comunes. No obstant això, Mathematica també disposa d'altres biblioteques més específiques que no es carreguen quan s'inicia el programa. La càrrega dels mateixos o dels Packages definits per a les seves necessitats específiques està a la disposició de l'usuari. Per exemple, suposem que hem definit les funcions “factorial” i “exponencial” en la llibreria “gurelib”.
DeclarePackage[“Calculus`gurelib`”,{”factorial”,”exponencial”}]
una vegada executada l'ordre, podrem utilitzar les operacions factorial i exponencial segons la norma d'ordre donada en la definició. La biblioteca que Mathematica té carregada a cada moment es guarda en la variable global $Packages.
Com no podia ser d'una altra manera, Mathematica també té la seva pròpia adreça Web, on es poden trobar informació, gràfics i últimes notícies: http://www.wolfram.com





