Mathématiques de Leonardo

Léonard de Vinci (1452-1519) est l'exemple des scientifiques de la Renaissance. Ce scientifique, comme on le sait, a été consacré à de nombreux domaines de la science: Anatomie, Optique, Botanique, Biologie, Géographie, Géologie, Mécanique, Géométrie, Peinture, Sculpture, Urbanisme, Architecture, Astronomie, Nautique, Physique, etc. Il n'y avait personne qui n'encouragerait à rechercher leurs curiosités. Je devais tout explorer.
Bien que plus connu dans les arts, nous ne pouvons pas exclure des contributions dans d'autres domaines. Léonard était autodidacte et, contrairement à d'autres scientifiques d'alors, il ne savait ni latin ni grec. Cependant, cela ne signifie pas que vos œuvres manquent d'une base solide. Au contraire, quand il plongeait dans une œuvre (science), il étudiait en profondeur toutes les formes. Sa curiosité était si grande qu'elle laissait souvent le travail qu'elle réalisait.
Nous savons que quand il est retourné à Florence en 1501, après avoir été avec Luca Pacioli, il a plongé dans la géométrie. Pendant ce temps, le tympan du tableau de Santa Ana ne cessa de faire. De 1501, il se consacre à la géométrie; entre 1504 et 1506 à l'hydraulique; en 1505, il a étudié la géométrie des solides dans un écrin; en 1510, il a été attiré par l'anatomie; etc.
Mais dans cet article, nous voulons mentionner les mathématiques de Leonardo, moins connu.
Le jeune Leonardo a beaucoup appris à l'école d'Andrea Verrocchio. Dans l'atelier de Verrocchio on étudiait non seulement la peinture, mais aussi le bronze fondu, la pierre, les plans, l'ouverture des canaux, la construction de maisons, etc. Dans tous ces “arts”, la connaissance de la perspective aussi dans la peinture avait une grande importance, on demandait une base scientifique (surtout mathématique) énorme. La formation de Leonardo était pratique, fondamentalement Ingénieur Leonardo, machiniste, non théorique. Par conséquent, il est de sa géométrie mécanique. Les solutions que vous recherchez sont pratiques (qui peuvent être faites avec des outils réels) et non théoriques.
Exemples de cette tendance pratique sont des études sur la construction de polygones réguliers inscrits en cercle. Dans ses écrits apparaissent ces images et de nombreuses propriétés. Entre autres choses, celles relatives au tableau du cercle; l'inscription des polygones de 3, 6, 8, 24 (c'est facile et Léonard le fait avec l'ouverture constante du compas), une approche de la construction des polygones réguliers (comme le Pentagone et l'haptágono qui ne peuvent pas être construits directement par des règles et des mesures, est plus difficile à réaliser, mais Léonard a suffisamment de solution étroite).
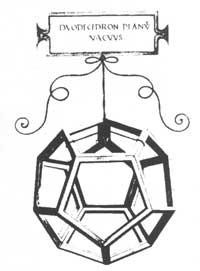
Probablement les pleins et vides de polyèdres réguliers et semi-réguliers qui illustrent le code “Divina Proportione” que Luca Pacioli offrit à Ludovico Mairua en 1498. Faites la direction du cercle et jetez un carré, un cercle ou un rouleau sur une droite ou un plan. Cette solution suppose une ignorance du problème théorique. Cependant, il est entendu du point de vue de l'ingénieur.
Sans doute, Léonard devait sa sagesse mathématique à Luca Pacioli. Et c'est qu'il l'a obtenu dès qu'il publiait Summa et a ensuite été réconcilié avec son auteur. Il a également rencontré Albert de Saxe, Jordanus Nemorarius (dont il faisait souvent référence) et Nicolas de Cusa (qui a certainement influencé lui). Il n'a certainement pas étudié directement à Archimède, mais il est clair qu'il l'a rencontré indirectement par Eutocio et Giorgio Valle.
Il est rare que vous n'ayez pas dîné de Leonardo Algebra. Était-ce difficile ou trop abstrait? Il était, cependant, une géométrie pure qui remplaçait la méconnaissance théorique de l'espace par son pouvoir visuel. Les réflexions sur les bases de la géométrie sont très intéressantes, bien que l'influence d'Aristote et Nicolas de Cusa est évidente.
Léonard ne recule pas devant l'utilisation de concepts infinitésimaux (c'est le passage à la limite). Par exemple, il propose de diviser le centre de gravité du demi-cercle en pyramides (triangles) de détermination, autant de pyramides que nécessaire pour que la fragilité de ses bases soit inappréciable et presque directe. Cependant, c'est un cas exceptionnel et, en général, les méthodes de Léonard sont plus simples, correctes et élémentaires.

Les idées intuitives, probablement, l'ont amené à sa plus grande découverte, à calculer le centre de gravité de la pyramide. Il semble qu'en déplaçant dans l'espace le même raisonnement qu'il a fait sur le centre de gravité du triangle du plan, en passant par le tétraèdre régulier, il a pu placer son centre de gravité au point de coupe de ses axes (c'est-à-dire les droites qui unissent un sommet au centre de gravité du côté opposé) et au quart de la distance de la base.


Plus tard, il a découvert que les droites qui unissent les points centraux des coins contre un tétraèdre sont coupés dans le centre de gravité. Enfin, il a généralisé la découverte, indiquant que le centre de gravité de toute pyramide se trouve sur son axe (de la base au quart).
Les recherches sur la transformation réciproque de solides sont basées sur “De transmutationibus geometricis” de Nicolas Cusa, qui applique les méthodes de Valle pour résoudre des problèmes énoncés par le Cusès (formant la confluence de plusieurs cubes, convertissant un cube en un prisme et vice versa). Cependant, Léonard considère également des transformations spéciales. Par exemple, entre le cube et la pyramide.
Léonard a également pris soin des lumules d'Hippocrate. En plus des nombreuses mentions de son Cahiers, en 1514, il a essayé d'écrire un traité: De ludo géométrique, il est resté incomplet comme tout son travail. On comprend qu'il existe une certaine passion pour la valeur esthétique des lumules. Au passage, en Occident, il découvre des propositions géométriques qui ne sont pas encore connues. Par exemple, il établit que la somme des surfaces des lumules construites sur les côtés des triangles équilatéraux était égale à celle du triangle.
Il convient de mentionner l'ingénieuse solution mécanique que Leonardo a trouvé pour le problème d'optique d'Al-Hazi avec une mesure spéciale. Cette solution de Leonardo indique une connaissance approfondie des propriétés des coupes coniques. Géométriquement 150 ans plus tard, il a été résolu par Huygens.
Les recherches sur la perspective de Léonard ont été publiées dans le «Traité de la peinture» en 1651.
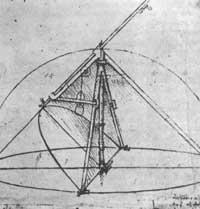
Il faut dire que Leonardo doit avoir des images et des projets d'outils mathématiques, des mesures proportionnelles et un parabole qu'il a utilisé pour construire des miroirs paraboliques.
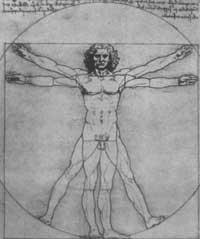
L'influence des mathématiques peut également être appréciée dans ses peintures. Leonardo a codifié les proportions du corps en faisant la géométrie infrastructure de ses peintures. Sa composition répond à un schéma harmonique facilement localisable, avec des structures radiales, troncs de cône, triangles, arcs, spirales, trapèzes, pentagones, etc.









