Leonardo's mathematics

Leonardo da Vinci (1452-1519) is the example of Renaissance scientists. This scientist, as is known, devoted himself to many fields of science: Anatomy, Optics, Botany, Biology, Geography, Geology, Mechanics, Geometry, Painting, Sculpture, Urbanism, Architecture, Astronomy, Nautical, Physics, etc. There was no one who would not encourage to investigate his curiosities. I had to explore everything.
Although it is best known in the arts, we cannot rule out contributions in other fields. Leonardo was self-taught and, unlike other scientists at the time, he knew neither Latin nor Greek. However, this does not mean that his works lack a solid foundation. On the contrary, when immersed in a work (science) he studied in depth all forms. His curiosity was so great that he often left the work he was doing.
We know that when he returned to Florence in 1501, after being with Luca Pacioli, he immersed himself in Geometry. Meanwhile, the tympanum of the Santa Ana painting did not stop doing. From 1501 he devoted himself to Geometry; between 1504 and 1506 to Hydraulics; in 1505 he studied the geometry of solids in a writing; in 1510 he was attracted by Anatomy; etc.
But in this article we want to mention the mathematics of Leonardo, less known.
Young Leonardo learned a lot in the school of Andrea Verrocchio. In Verrocchio's workshop we studied not only painting, but also cast bronze, stone, plans, opening channels, building houses, etc. In all these “arts”, the knowledge of perspective also in painting was of great importance, a huge scientific (mostly mathematical) basis was demanded. Leonardo's training was practical, fundamentally Leonardo Engineer, machinist, not theoretical. Therefore, it is of its mechanical geometry. The solutions you are looking for are practical (that can be done with real tools) and not theoretical.
Examples of this practical trend are studies on the construction of regular polygons inscribed in circle. These images and many properties appear in his writings. Among other things, those related to the circle picture; the inscription of the polygons of 3, 6, 8, 24 (it is easy and Leonardo does it with the constant opening of the compass), an approximation to the construction of the regular polygons (such as the pentagon and the haptagon that cannot be built directly by rules and compasses, is more difficult to realize, but Leonardo has enough close solution).
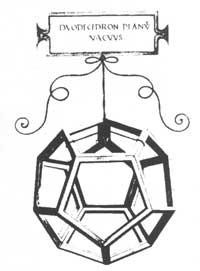
Probably the full and empty regular and semi-regular polyhedra that illustrate the “Divina Proportione” code that Luca Pacioli offered to Ludovico Mairua in 1498 will be yours. Make the direction of the circle and throw a square, circle or roller over a straight line or plane. This solution implies a lack of knowledge of the theoretical problem. However, it is understood from the point of view of the engineer.
Without a doubt, Leonardo owed his mathematical wisdom to Luca Pacioli. He got it as soon as he published Summa and then reconciled with his author. He also met Albert of Saxony, Jordanus Nemorarius (whom he often referred to) and Nicholas of Cusa (who undoubtedly influenced him). Surely he did not study Archimedes directly, but it is clear that he knew him indirectly through Eutocio and Giorgio Valle.
It is rare that I have not had dinner with Leonardo Algebra. Was it difficult or too abstract? It was, however, a pure geometry that replaced the theoretical ignorance of space by its visual power. The reflections on the basic concepts of geometry are very interesting, although the influence of Aristotle and Nicholas of Cusa is evident.
Leonardo does not retreat from the use of infinitesimal concepts (it is the step to the limit). For example, it proposes dividing the center of gravity of the semicircle into pyramids (triangles) of determination, as many pyramids as necessary so that the fragility of its bases is invaluable and almost direct. However, this is an exceptional case and, in general, Leonardo's methods are simpler, correct and elementary.

Intuitive ideas probably led him to his greatest discovery, to calculate the center of gravity of the pyramid. It seems that by moving into space the same reasoning he made about the center of gravity of the plane triangle, passing through the regular tetrahedron, he was able to locate his center of gravity at the cutting point of his axes (i.e., the straight lines that link a vertex with the center of gravity on the opposite side) and the quarter of the distance from the base.


He later discovered that the straight lines linking the center points of the corners against a tetrahedron are cut into the center of gravity. Finally, he generalized the discovery, indicating that the center of gravity of any pyramid is at its axis (from the base to the fourth part).
The research on the reciprocal transformation of solids is based on “De transmutationibus geometricis” by Nicolás Cusa, who applies the methods of Valle to solve problems enunciated by the cusés (forming the confluence of several cubes, turning a cube into a prism and vice versa). However, Leonardo also considers special transformations. For example, between the cube and the pyramid.
Leonardo also took care of the Hippocrates. In addition to the numerous mentions of his Notebooks, in 1514 he tried to write a treatise: Of geometric ludo, which remained incomplete as all his work. It is understood that there is a certain passion for the aesthetic value of lumula. Incidentally, in the West he discovered geometric propositions that were not yet known. For example, he established that the sum of the surfaces of the lumens built on the sides of the equilateral triangles was equal to that of the triangle.
It is worth mentioning the ingenious mechanical solution that Leonardo found for the Al-Hazi Optics problem with a special compass. This solution by Leonardo indicates deep knowledge about the properties of conical cuts. Geometrically 150 years later it was resolved by Huygens.
Leonardo’s research on perspective was published in the “Painting Treaty” in 1651.
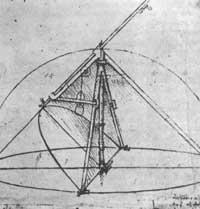
It must be said that Leonardo is owed images and projects of mathematical tools, measure of proportion and a parabolograph that he used to build parabolic mirrors.
The influence of mathematics can also be seen in his paintings. Leonardo codified the proportions of the body making the infrastructure geometry of his paintings. Its composition responds to an easily localizable harmonic scheme, with radial structures, cone trunks, triangles, arches, spirals, trapeziums, pentagons, etc.









